
dH Tx +H=K×qwl dt 静态:流入水槽的流量qV1等于流出水槽的流量 V2,液位稳定在某一数值Ho上,处于平衡状态。 动态:在to时刻,进口流量qv1突然有一阶跃变化 量△qv1,可由上式求出相应的液位变化量:
静态: 流入水槽的流量qv1等于流出水槽的流量 qv2,液位稳定在某一数值H0上,处于平衡状态。 动态:在t0时刻,进口流量qv1突然有一阶跃变化 量Δqv1,可由上式求出相应的液位变化量: 1 dH T H K qv dt

△H=K×△gwl1-e-o/T (2-7) 根据上式画出水槽液位在阶跃激励作用下的单 容自衡特性曲线: h . qv 0 F to 0.3第 H 1 H∞ 0.20 0.0 Ho 有自衡特性液位变化曲线 to A一一流量曲线 B一一高位槽液位曲线
根据上式画出水槽液位在阶跃激励作用下的单 容自衡特性曲线: 0 ( )/ 1(1 ) t t T H K qv e (2-7)
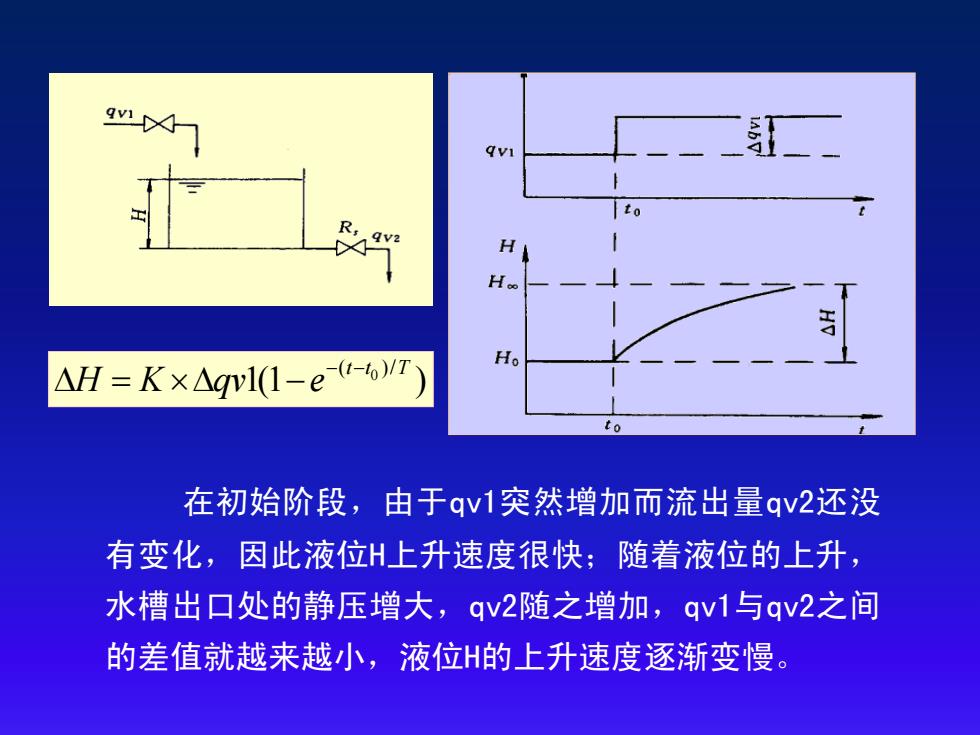
H 1 △H=K×△gwl1-et-6/r Ho to 在初始阶段,由于qv1突然增加而流出量qv2还没 有变化,因此液位H上升速度很快;随着液位的上升, 水槽出口处的静压增大,qv2随之增加,qv1与qv2之间 的差值就越来越小,液位H的上升速度逐渐变慢
在初始阶段,由于qv1突然增加而流出量qv2还没 有变化,因此液位H上升速度很快;随着液位的上升, 水槽出口处的静压增大,qv2随之增加,qv1与qv2之间 的差值就越来越小,液位H的上升速度逐渐变慢。 0 ( )/ 1(1 ) t t T H K qv e
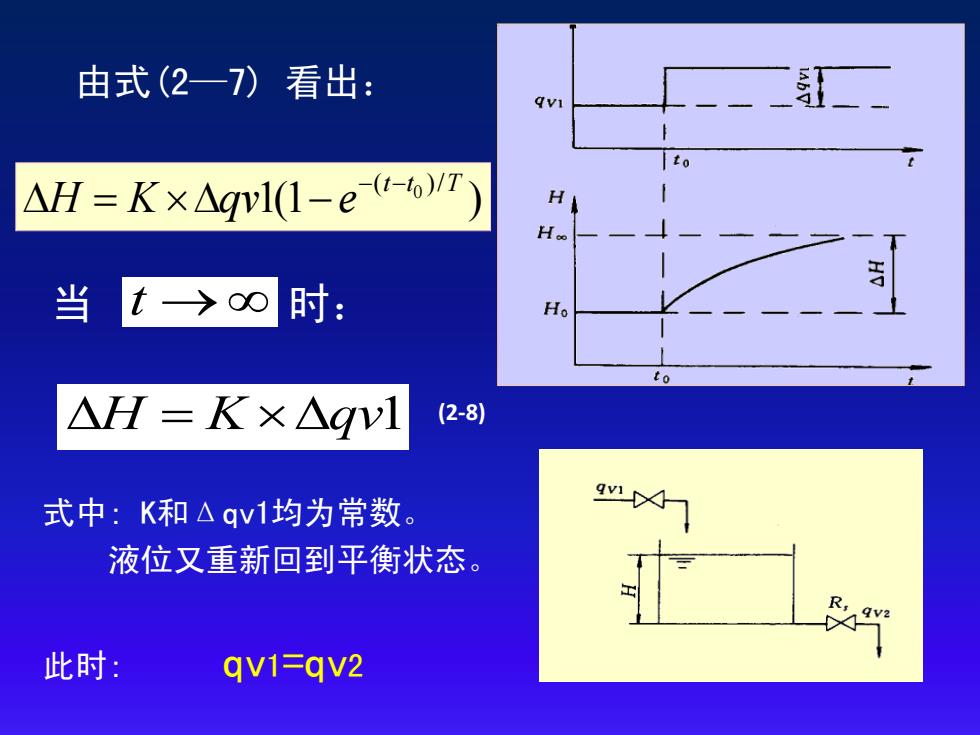
由式(2一7)看出: qvi to △H=Kx△glI-et-6/T) H Ho 当 t>0 时: Ho to △H=K×△gv1 (2-8) 式中:K和△qv1均为常数。 液位又重新回到平衡状态。 ,4y2 此时: qv1=qv2
H K qv1 (2-8) 式中: K和Δqv1均为常数。 液位又重新回到平衡状态。 此时: qv1=qv2 由式(2—7) 看出: 当 t 时: 0 ( )/ 1(1 ) t t T H K qv e
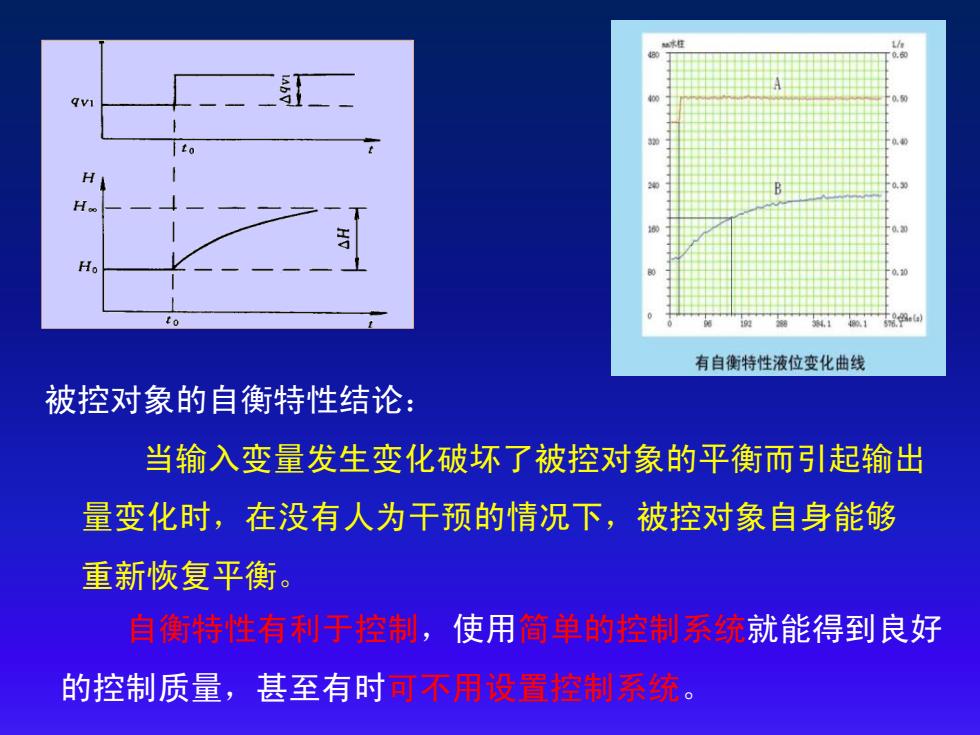
qvi H H 0.3 561.1 0.1) 有自衡特性液位变化曲线 被控对象的自衡特性结论: 当输入变量发生变化破坏了被控对象的平衡而引起输出 量变化时,在没有人为干预的情况下,被控对象自身能够 重新恢复平衡。 自衡特性有利于控制,使用简单的控制系统就能得到良好 的控制质量,甚至有时可不用设置控制系统
被控对象的自衡特性结论: 当输入变量发生变化破坏了被控对象的平衡而引起输出 量变化时,在没有人为干预的情况下,被控对象自身能够 重新恢复平衡。 自衡特性有利于控制,使用简单的控制系统就能得到良好 的控制质量,甚至有时可不用设置控制系统