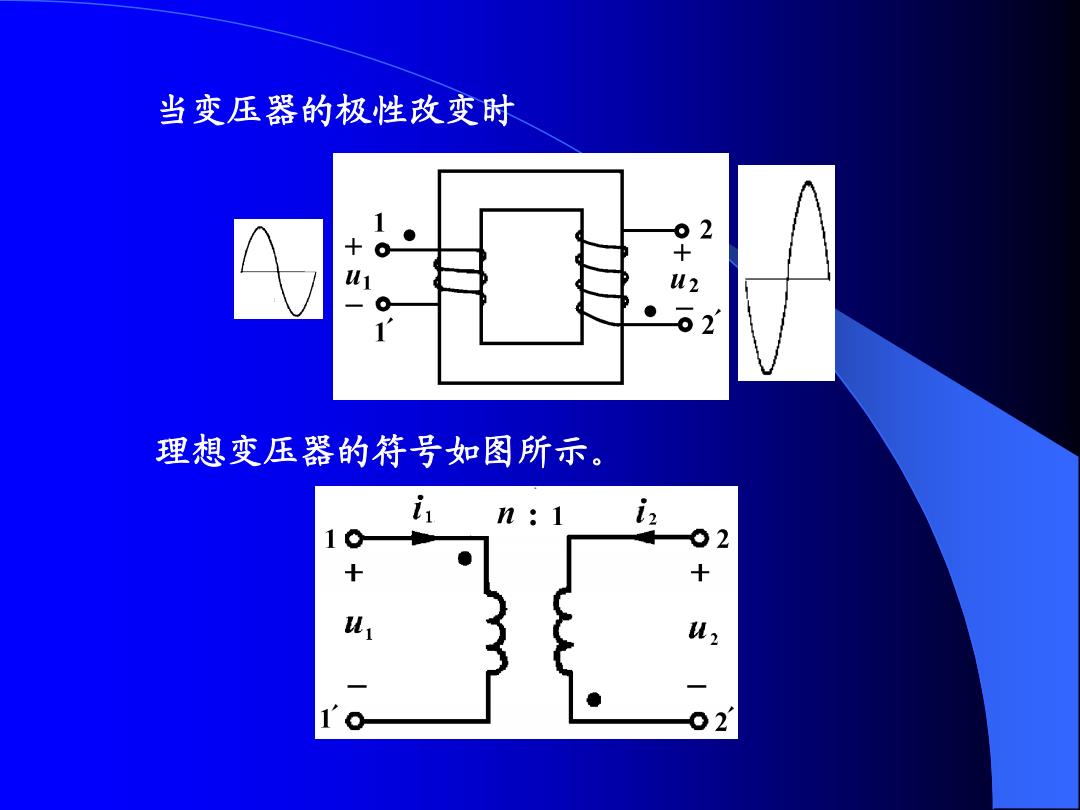
当变压器的极性改变时 0+ 2 2 理想变压器的符号如图所示。 l n:1 02 u
理想变压器的符号如图所示。 当变压器的极性改变时

n:1 12 02 理想变压器的电压电流关系为: u=-nu (5-3) 12 =ni (5-4) 表征理想变压器端口特性的VCR方程是两个线性代数 方程,因而理想变压器是一种线性双口电阻元件。与实际 变压器不同。它既可工作于交流又可工作于直流,对电压、 电流的频率和波形没有任何限制
理想变压器的电压电流关系为: (5 4) (5 3) 2 1 1 2 i ni u nu 表征理想变压器端口特性的VCR方程是两个线性代数 方程,因而理想变压器是一种线性双口电阻元件。与实际 变压器不同。它既可工作于交流又可工作于直流,对电压、 电流的频率和波形没有任何限制

n:1 12 92 u =nu (5-1) 1=-ni (5-2) 理想变压器有两个基本性质: 1.理想变压器既不消耗能量,也不储存能量,在任 时刻进入理想变压器的功率等于零,即 p=4i+422=nu2i-w2ni=0 此式说明从初级进入理想变压器的功率,全部传输到 次级的负载中,它本身既不消耗,也不储存能量
此式说明从初级进入理想变压器的功率,全部传输到 次级的负载中,它本身既不消耗,也不储存能量。 p u1 i 1 u2 i 2 nu2 i 1 u2 ni1 0 理想变压器有两个基本性质: 1.理想变压器既不消耗能量,也不储存能量,在任一 时刻进入理想变压器的功率等于零,即 (5 2) (5 1) 2 1 1 2 i ni u nu

2.当理想变压器次级端接一个电阻R时,初级的输入 电阻为n2R。 n:1 n'R 图5-2 用外加电源法求得图示单口网络的输入电阻为 R 11 n
2.当理想变压器次级端接一个电阻R时,初级的输入 电阻为n 2R。 图5-2 用外加电源法求得图示单口网络的输入电阻为 (5 5) 2 2 2 2 2 2 1 1 i n R i u n n i n u i u R

h:1 i a n'R bo R 4= nu2 2 FnR5-5列 n 上式表明理想变压器不仅可以变换电压和电流,也可 以变换电阻。可以证明,式(5-5)的结论与理想变压器 初、次级极性标记的位置无关,因此今后在这种情况下可 以不标出初、次级的极性
(5 5) 2 2 2 2 2 2 1 1 i n R i u n n i n u i u R 上式表明理想变压器不仅可以变换电压和电流,也可 以变换电阻。可以证明,式(5-5)的结论与理想变压器 初、次级极性标记的位置无关,因此今后在这种情况下可 以不标出初、次级的极性