
中的分组码。 A vector of K input W/2 complex bits symbols P/S To QAM Constellation modulator Fig5.1.5 Another way is to extend the dimensionality of the transmitted signal by basing it on a achine (M)Theedd the PM mpnhrent increase in the number of points in the FSM k+r selecto Information Subset label bit sequence (e Coded signal m-k Signal point sequence selector Mapper function x=f(c) Fig.5.1.6 5.1.2 Overview ofCoded Modulation Techniques The existing coded modulation schemes for band-limited AWGN channels can be broadly classified into four categories: 1)Lattice codes 2)Trellis/TCM codes(trellis-coded modulation) TCM was proposed by Ungerboeck is usuallyused as the underlying FSM.The term trellis-coded modulation originates from the fact that these coded sequences consist of modulated symbols rather than binary digits.In other words,in TCM schemes,the trellis branches are labeled with redundant nonbinary modulated symbols rather than with binary coded symbols tcm codes can be decoded by naximu m-likelihood de sing Viterbi alg Trellis codes are to lattices as binary convolutionl codes are to block codes 3)Turbo-TCM 4)Multilevel codes(also known as BCM) Multilevel codes was proposed by H.Imai in 1977.The underlying strategy is to protect 5-6
5-6 中的分组码。 N-dimensional Constellation P/S K input bits A vector of N/2 complex symbols To QAM modulator Fig. 5.1.5 Another way is to extend the dimensionality of the transmitted signal by basing it on a finite-state machine (FSM). The extra bits produced by the FSM implies an inherent increase in the number of points in the constellation. FSM Constellation selector Signal point selector k k+r m-k Mapper function x=f(c) Coded signal sequence {xi } m bits per symbol Information bit sequence Subset label sequence {ci } Fig. 5.1.6 5.1.2 Overview of Coded Modulation Techniques The existing coded modulation schemes for band-limited AWGN channels can be broadly classified into four categories: 1) Lattice codes 2) Trellis/TCM codes (trellis-coded modulation) TCM was proposed by Ungerboeck in 1982, in which a convolutional code is usually used as the underlying FSM. The term trellis-coded modulation originates from the fact that these coded sequences consist of modulated symbols rather than binary digits. In other words, in TCM schemes, the trellis branches are labeled with redundant nonbinary modulated symbols rather than with binary coded symbols. TCM codes can be decoded by a maximum-likelihood decoder using Viterbi algorithm. Trellis codes are to lattices as binary convolutional codes are to block codes. 3) Turbo-TCM 4) Multilevel codes (also known as BCM) Multilevel codes was proposed by H. Imai in 1977. The underlying strategy is to protect

each label bit of the signal point by an individual binary code,so mutiple encoders (at different levels)are employed.At the receiver,the received sequence of signal points are sually decoded by a multis age decoder In multilevel coding(MLC)schemes,any code,e.g,block codes,convolutional codes,or concantenated codes.can be used as component codes.Since in early MLC schemes the FEC codes used were usually block codes,the MLC scheme is also referred to as block coded modulation (BCM) 5)Bit-interleaved coded modulation(BICM)(with iterative decoding) BICM was first proposed by Zehavi in199 for coding for fading channels,in which the output stream of a binary encoder is bit-interleaved and then mapped to an M-ary constellation.Its basic idea is to increase the code diversity.(For Rayleigh fading channels, the code performance depends strongly its minimum Hamming distance rather than the minimum Euclidean distance.)The information-theoretic aspects of BICM have been analyzed by Caire Recently,it has been recognized that the BICM based on turbo-like codes and iterative decoding provides an effective realization method for Gallager's coding theorem(proposed in 1968 for discrete memoryless channels).With this scheme,very good performance can be achieved on both awgn and fading channels Fig.5.1.7 depicts the performances of some of typical coded modulation schemes 7 M-QAM bound V33 64-QAM <4M4.37 32.0AM ·e0(4,3 + 16QAM 404,36) BPSK 43为 TCW32.7刀Mc OPSK P=10 40 12 14 16 20 E/N (dB) spectral efficiencies achieved by 5.2 Coding Gain and Shaping Gain In coded modulations,we can use the following approaches for improving signal 5.7
5-7 each label bit of the signal point by an individual binary code, so mutiple encoders (at different levels) are employed. At the receiver, the received sequence of signal points are usually decoded by a multistage decoder. In multilevel coding (MLC) schemes, any code, e.g., block codes, convolutional codes, or concantenated codes, can be used as component codes. Since in early MLC schemes the FEC codes used were usually block codes, the MLC scheme is also referred to as block coded modulation (BCM). 5) Bit-interleaved coded modulation (BICM) (with iterative decoding) BICM was first proposed by Zehavi in 1992 for coding for fading channels, in which the output stream of a binary encoder is bit-interleaved and then mapped to an M-ary constellation. Its basic idea is to increase the code diversity. (For Rayleigh fading channels, the code performance depends strongly its minimum Hamming distance rather than the minimum Euclidean distance.) The information-theoretic aspects of BICM have been analyzed by Caire. Recently, it has been recognized that the BICM based on turbo-like codes and iterative decoding provides an effective realization method for Gallager’s coding theorem (proposed in 1968 for discrete memoryless channels). With this scheme, very good performance can be achieved on both AWGN and fading channels. Fig. 5.1.7 depicts the performances of some of typical coded modulation schemes. Figure 5.1.7: Theoretical limits on spectral and power efficiency for different signal constellations and spectral efficiencies achieved by various coded and uncoded transmission methods. 5.2 Coding Gain and Shaping Gain In coded modulations, we can use the following approaches for improving signal

constellation designs ■The first idea he agonal (Alternatively,we could keep the variance constant,in which case the hexagonal constellation would have a larger minimum distance than the squared constellation.)This decrease in power for the same minimum distance or increase in minimum distance for the same power through changing the relative spacing of the points is called codinggain The 2nd approach is to change the shape or outline of the constellation without changing the relative positioning of points.The circular constellation will have a lower variance than the squared constellation.On the same grounds.a circular constellation will have the lowest variance of any shaping region for a square grid of points.The resulting reduction in power is called shaping gain Significantly,shaping onstellation changes the marginal density of the data symbol This isillustrated in Fig.5.9 Coding and shaping gain can be combined.e.g.by changing the points in the circularly shaped constellation to a hexagonal grid while retaining the circular shaping. Usually,channel coding deals with the internal arrangement of the points,whereas The egions idea is to employ multidimensional signal constellation.A data symbol drawn from an N-dim constellation is transmitted once every N2 signaling interval.When we design a 2D constellation,and choose the N/2 successive symbols to be an arbitrary sequence of 2D symbols drawn from that constellation,the resulting N-dim constellation is the N2-fold Cartesian product of 2D constellations.From Chapter2,we know that the nance of this N-dim tellation is the san as the und erlying2D。 ation llation that is not constrained to have this Cartesian product structure.When N>2,it is called a multidimensional signal constellation. Greater shaping and coding gains can be achieved with a multidimensional signal onstellation than with a 2D constellation.How eve multidim ensional constellations from a complexity that increases exponentially with dimensionality Square Hexagonal Circular Fig 5.8 Three 2D constellations with the same minimum distance and 256 points 5-8
5-8 constellation designs. The first idea is to change the relative spacing of points in the constellation. The hexagonal constellation leads to the reduced variance with the same minimum distance. (Alternatively, we could keep the variance constant, in which case the hexagonal constellation would have a larger minimum distance than the squared constellation.) This decrease in power for the same minimum distance or increase in minimum distance for the same power through changing the relative spacing of the points is called coding gain. The 2nd approach is to change the shape or outline of the constellation without changing the relative positioning of points. The circular constellation will have a lower variance than the squared constellation. On the same grounds, a circular constellation will have the lowest variance of any shaping region for a square grid of points. The resulting reduction in power is called shaping gain. Significantly, shaping the constellation changes the marginal density of the data symbol. This is illustrated in Fig. 5.9. Coding and shaping gain can be combined, e.g., by changing the points in the circularly shaped constellation to a hexagonal grid while retaining the circular shaping. Usually, channel coding deals with the internal arrangement of the points, whereas shaping treats regions. The 3rd idea is to employ multidimensional signal constellation. A data symbol drawn from an N-dim constellation is transmitted once every N/2 signaling interval. When we design a 2D constellation, and choose the N/2 successive symbols to be an arbitrary sequence of 2D symbols drawn from that constellation, the resulting N-dim constellation is the N/2-fold Cartesian product of 2D constellations. From Chapter 2, we know that the performance of this N-dim constellation is the same as the underlying 2D constellation. An alternative is to design an N-dim signal constellation that is not constrained to have this Cartesian product structure. When N>2, it is called a multidimensional signal constellation. Greater shaping and coding gains can be achieved with a multidimensional signal constellation than with a 2D constellation. However, multidimensional constellations suffer from a complexity that increases exponentially with dimensionality. Square Hexagonal Circular Fig.5.8 Three 2D constellations with the same minimum distance and 256 points
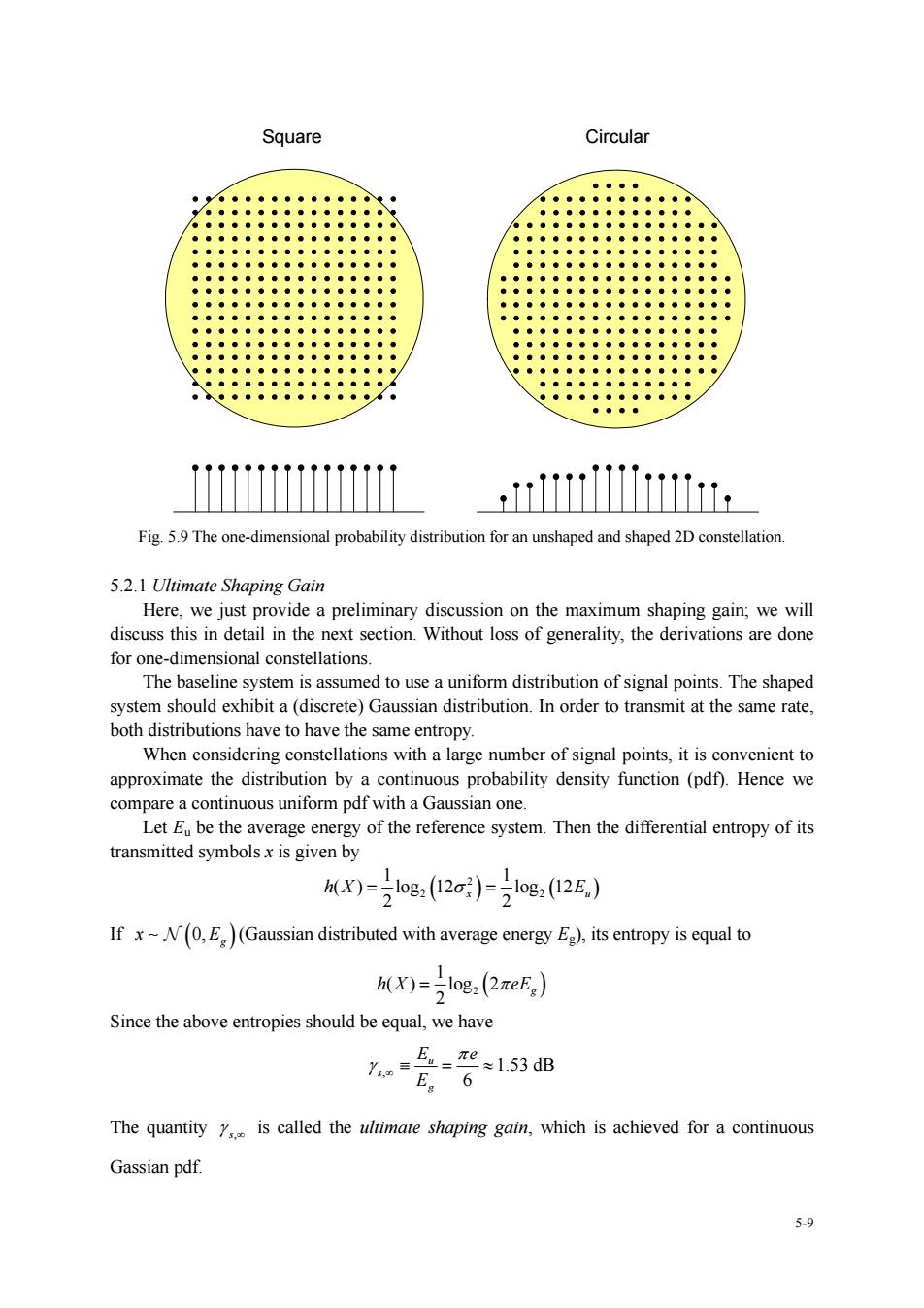
Square Circular Fig.59The one-dimensional probability distribution for an unshaped and shaped 2D constellation 5.2.1 Ultimate Shaping Gain Here,we just provide a preliminary discussion on the maximum shaping gain,we will discuss this in detail in the next section.Without loss of generality,the derivations are done for one-dimensional constellations ystem is ass med to use auniform distribution of signal points.The shaped ystemshou(disrete) both distributions have to have the same entropy. When considering constellations with a large number of signal points,it is convenient to approximate the distribution by a continuous probability density function(pdf).Hence we ompare a continuous uniform pdf with a Gaussian one. Let Ebe the verage energy of the reference system.Then the differential entropy of its transmitted symbolsx is given by MX)=g:2c)=g:2E) If x-N(0,E)(Gaussian distributed with average energy E).its entropy is equal to h(X)=log2(2πeE) Since the above entropies should be equal,we have E2-形=1.53dB 6 The quantity is called the ultimate shaping gain,which is achieved for a continuous Gassian pdf. 5.9
5-9 Square Circular Fig. 5.9 The one-dimensional probability distribution for an unshaped and shaped 2D constellation. 5.2.1 Ultimate Shaping Gain Here, we just provide a preliminary discussion on the maximum shaping gain; we will discuss this in detail in the next section. Without loss of generality, the derivations are done for one-dimensional constellations. The baseline system is assumed to use a uniform distribution of signal points. The shaped system should exhibit a (discrete) Gaussian distribution. In order to transmit at the same rate, both distributions have to have the same entropy. When considering constellations with a large number of signal points, it is convenient to approximate the distribution by a continuous probability density function (pdf). Hence we compare a continuous uniform pdf with a Gaussian one. Let Eu be the average energy of the reference system. Then the differential entropy of its transmitted symbols x is given by ( ) ( ) 2 2 2 1 1 ( ) log 12 log 12 2 2 x u hX E = = σ If ( ) 0, g x ∼ N E (Gaussian distributed with average energy Eg), its entropy is equal to 2 ( ) 1 ( ) log 2 2 g h X eE = π Since the above entropies should be equal, we have , 1.53 dB 6 u s g E e E π γ ∞ ≡=≈ The quantity s, γ ∞ is called the ultimate shaping gain, which is achieved for a continuous Gassian pdf

5.3 Lattice Constellations It is from Shannon's capacity theorem that an optimal block code for a bandwidth-limited AWGN channel consists of a dense packing of code points within a sphere in a high-dimensional Euclidean space.Most of the densest known packings are lattices. An n-dimensional (n-D)lattice A is an infinite discrete set of points(vectors,n-tuples)in the real Euclidean n-space R"that has the group property. Example 5.3.1:The set of all integers,=,is a one-dimensional lattice,since is a discrete subgroup of R.The set 22 of all integer-valued two-tuples(m,n)with n Z is a 2-dimensional lattice.More generally,the set Z"of all integer-valued n-tuples is an n-D lattice. The lattice RZ.whereR1 1-1A is obtained by rotating Z2 by /4 and scaling by √5.Clearly,R2z2=2z Definition I:Let g1sjsm be a set of linearly independent vectors in R"(so that msn).The set of points ==2,e2 (5.1) is called an m-dimensional lattice,and gsmis called a basis of the lattice. That is,A是基向量的整数线性组合。The matrix withg,as rows g G Lg. is called a generator matrix for the lattice.在后续讨论中,we will deal with full-rank lattices. i.e.,m=n.So a general n-D lattice that spans R"may be expressed as A=x=aGaeZ" (5.1) 例如,the lattice2 has the generator-0] 10 A coset of a lattice A,denoted by A+x,is a set of all points obtained by adding a fixed point x to all lattice points aA.Geometrically,the coset A+x is a translate of A by x.If 文10
5-10 5.3 Lattice Constellations It is known from Shannon’s capacity theorem that an optimal block code for a bandwidth-limited AWGN channel consists of a dense packing of code points within a sphere in a high-dimensional Euclidean space. Most of the densest known packings are lattices. An n-dimensional (n-D) lattice Λ is an infinite discrete set of points (vectors, n-tuples) in the real Euclidean n-space Rn that has the group property. Example 5.3.1: The set of all integers, {0, 1, 2,.} Z = ± ± , is a one-dimensional lattice, since Z is a discrete subgroup of R. The set Z2 of all integer-valued two-tuples (n1, n2) with i n ∈Z is a 2-dimensional lattice. More generally, the set Zn of all integer-valued n-tuples is an n-D lattice. The lattice RZ2 , where 1 1 1 1 R ⎡ ⎤ = ⎢ ⎥ ⎣ ⎦ − , is obtained by rotating Z2 by π/4 and scaling by 2 . Clearly, R2 Z2 = 2Z2 . Definition 1: Let { ,1 } j g ≤ ≤j m be a set of linearly independent vectors in Rn (so that m n ≤ ). The set of points 1 m jj j j a a = ⎧ ⎫ Λ= = ∈ ⎨ ⎬ ⎩ ⎭ x g ∑ Z (5.1) is called an m-dimensional lattice, and { ,1 } j g ≤ j m≤ is called a basis of the lattice. That is, Λ是基向量的整数线性组合。The matrix with gj as rows 1 2 m G ⎡ ⎤ ⎢ ⎥ = ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ g g g # is called a generator matrix for the lattice. 在后续讨论中,we will deal with full-rank lattices, i.e., m=n. So a general n-D lattice that spans Rn may be expressed as { }n Λ= = ∈ xaa G Z (5.1) 例如,the lattice Z2 has the generator 1 0 0 1 G ⎡ ⎤ = ⎢ ⎥ ⎣ ⎦ . A coset of a lattice Λ, denoted by Λ+x, is a set of all points obtained by adding a fixed point x to all lattice points a∈Λ. Geometrically, the coset Λ+x is a translate of Λ by x. If