
并用R描述所有可能的运动, 解:a部=(号m) =m=…(-ge2X)=0, 即T是运动常数, )j=(mwx+) =mX+m啡X+g+(-)”; -mrxr+fagraorc --gerx(xr)+gerx(axr)-0. 即J为运动常数,其中利用=…7r×(4×)=… r)-r(r·) (@)rJ=rJ1coa=r(mr×+eg)=egr,得 cos=号=常量. 即带电粒子必在张角为的直立圆锥表面上运动。 周R=aExx 克=aex× %

利用r×=L/m,L=J-e0号和m=-9eX”,有 m成=ag3×[(J-0;)×], “1×-器对] 部 再利用R=r,得R的运动方程 m成-黑R 写成分量形式 m(成-R)=-器, m(R节+2p)=0, (mR9)=j=0, m成。-器+最,. 其中J=mR中=常量, e'g2 1R=.+2i2rW-eg) 品-(-) cg近六 2m 31

伴用守恒量 合n成:+.)=2nR+K毫=B(常登, 中=mR· 其中K=eg2tg/2m,消去dt得: 器=生明√层E-K). 积分得: ±[g√层R-1-g√侵-i]-(p-,> =8in5(p-p,). 此方程描述了R一中的关系,即为运动方程. 由于有效势是一个斥力势,所以不管初始状态如何,最 后R都趋向无限远 (王球) 1030(MIT,1979) 巴黎和伦敦用一条直的地下铁道联结。两城市间的火车 在重力作用下运行。计算火事的最大速度以及从伦敦到巴黎 旅行所需时间。两城市间距离为300km,地球半径为6400km, 忽略摩擦.(图1.19) 解:在地球内重力势能为(-3R,共中M为 地球质量,m为火車质量,根据机械能守恒,有关系, 是m+(-3R=-SmM 32
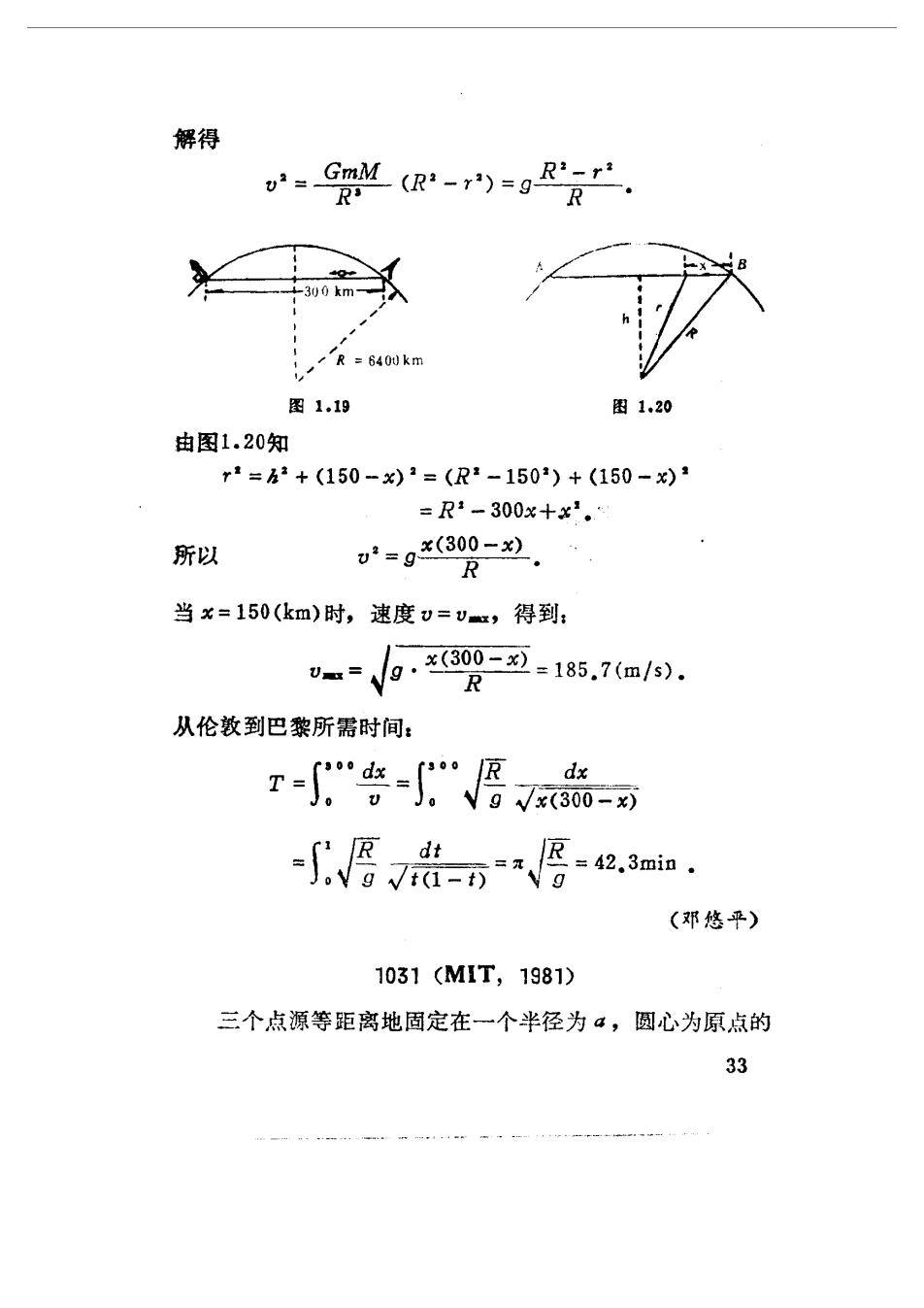
解得 =(R)=R R 图1.19 图1.20 由图1.20知 r=2+(150-x)=(R2-150*)+(150-x) =R1-300x+x2. 所以 2=g¥(300-x) R 当×=150(km)时,速度v=vx,得到: ”m=√g.809-五=185.70m/. R 从伦敦到巴黎所需时间: r-告… dx = dt 区=42.3min· (邓悠平) 1031(MIT,1981) 三个点源等距离地固定在一个半径为,圆心为原点的 33

圆周上。每个点源对质点(质量为)的作用力是吸引力 F=一kR,其中R是从点源指向质点的矢量,质点在t=0 时刻被放入力场,初始条件是:r=r。,·=”。.(初始情况 如图1.11)· (a)选择适当的坐标,并写出在任意时刻作用在质点上 的力的表达式. (b)利用牛頓第二定律,在上述初始条件下解运动方 程,即用r。,。以及其它系统参数表示r(t) (©)在什么条件下(如果存在的話)圆轨道是一种解. 解:(a)以圆心为原点时,可以直接写出矢量表达式。 记r1,r:,T,分别为三个点源的矢径,由题给的条件, 必有 r,+r,+r,=0 质点m所受的力为 F=-(r-r:)-(r-r) -(r-r,)=-3r. (b)运动方程为 m7=-3r, 即 m萨+3r=0. 图1.21 直接得到通解: ()aco(V祭)+bsin(√既) 由初始条件:t=0时,r(0)=r,t(@)=心。可确定出:a= 6=√0,最后得解: r=reo(√既)+√,(V既 34