同济大学：《结构动力学》课程教学资源（教案讲义）Lecture 05 Response to Arbitrary, Step , and Pulse Excitations

Structural Dynamics Lecture 5: Response to Arbitrary,Step and Pulse Excitations 目 19 同桥大学 本之程学成

Structural Dynamics Lecture 5: Response to Arbitrary, Step , and Pulse Excitations

Contents Response of SDOF to arbitrary excitation ·Duhamel's integral Response to Special Force Types ·Step Force Ramp or Linearly Increasing Force ·Step Force ·Impulsive Force 目 土本鞋李悦

Contents  Response of SDOF to arbitrary excitation • Duhamel’s integral  Response to Special Force Types • Step Force • Ramp or Linearly Increasing Force • Step Force • Impulsive Force

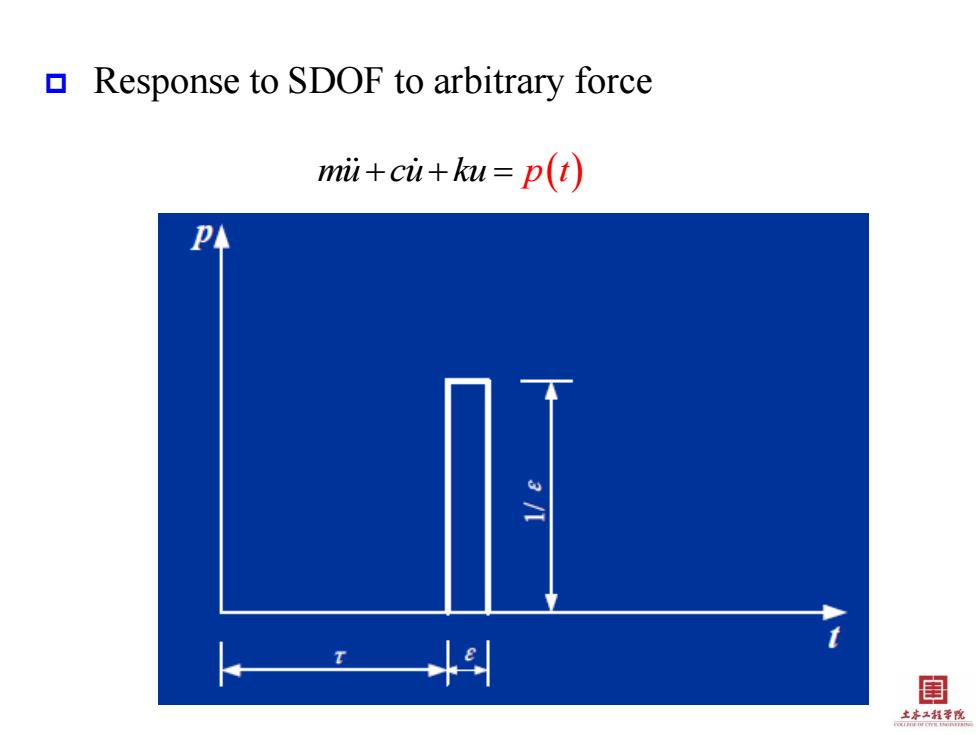
Response to SDOF to arbitrary force mii+cu+ku=p(t) PA 目 土茅红指等院

 Response to SDOF to arbitrary force mu cu ku    p t 

▣Duhamel's integral mii+cu+ku=p(t) u(t)=p()h(i-z)dz 。 Duhamel's integral(convolution integral or superposition integral)is a well-known approach to the solution of transient (or arbitrary load)vibration problems in linear systems.Its development is based on the superposition of the response of the system to a sequence of impulse. Response to unit impulse Unit impulse-response function h-)=2sn[a,t-】1≥r m0, -小.-l12 目 土本程李悦

 Duhamel’s integral • Duhamel’s integral (convolution integral or superposition integral) is a well-known approach to the solution of transient (or arbitrary load) vibration problems in linear systems. Its development is based on the superposition of the response of the system to a sequence of impulse.  Response to unit impulse • Unit impulse-response function         0 t mu cu ku u p t d p t t h                1 sin n t D D h t e t t m                      1 sin n n h t t t m             

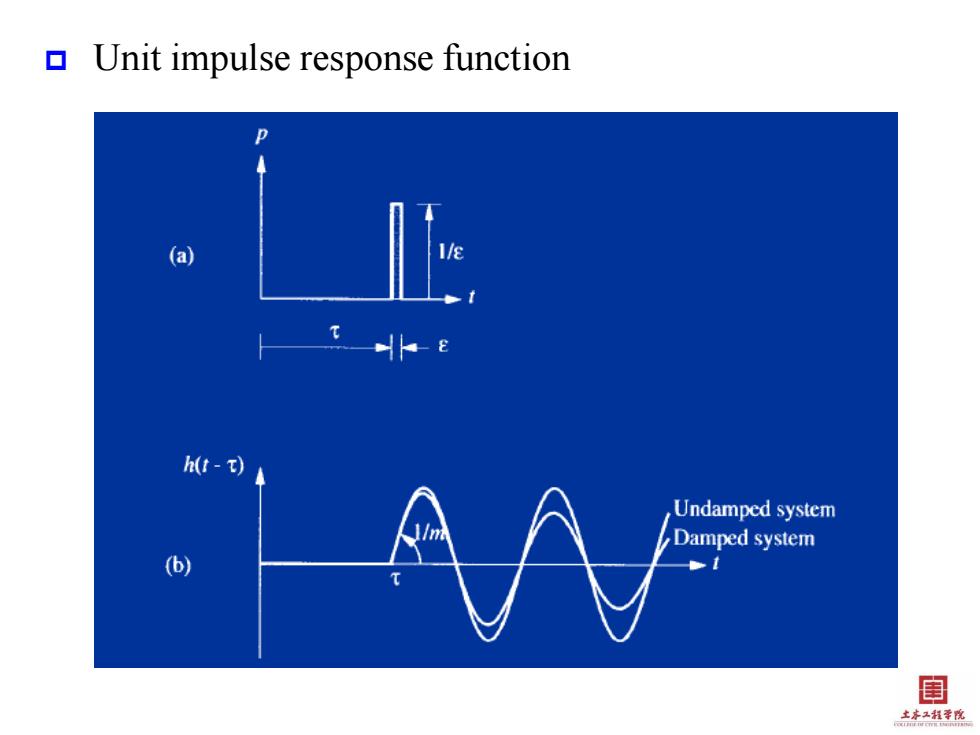
Unit impulse response function (a) h(t-t) Undamped system Damped system b)》 目 土李红程季悦

 Unit impulse response function