
Structural Dynamics Lecture 6 Numerical Evaluation of Dynamic Response 自 同海大学 土本工相学院
Structural Dynamics Lecture 6 Numerical Evaluation of Dynamic Response
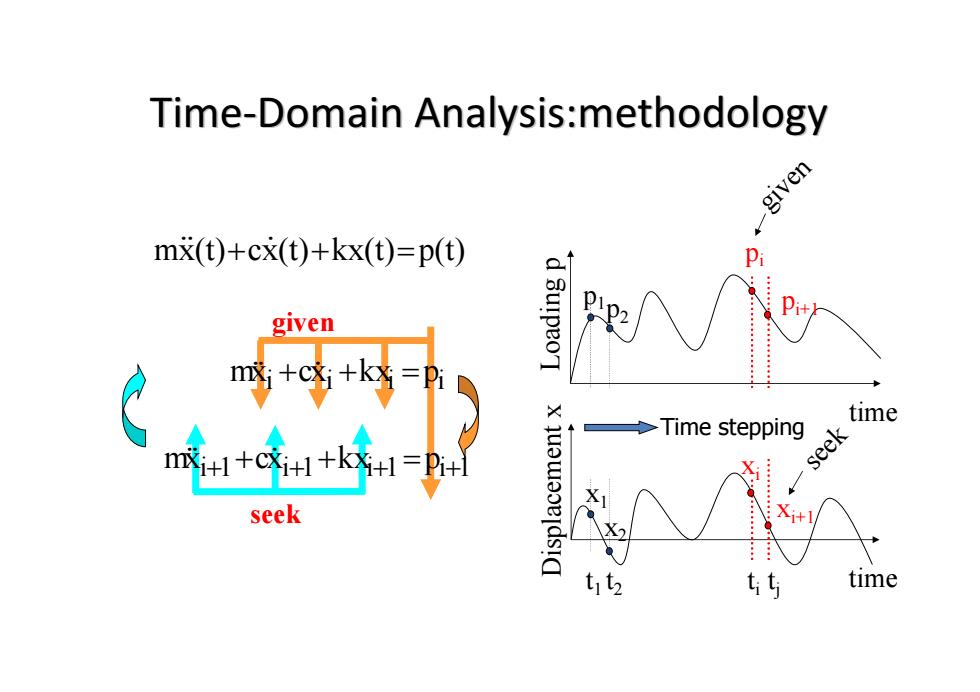
Time-Domain Analysis:methodology given m(t)+cx(t)+kx(t)=p(t) Pi given 'd 3u!peoT p} m++k= time Time stepping m++c++k=+ seek seek time
Time-Domain Analysis:methodology Time-Domain Analysis:methodology mx(t)cx(t)kx(t)p(t) L o a d i n g p time D i s p l a c e m e n t x time p1 x1 t1 p2 x2 t2 given seek i xi kxi pi mx c i 1 xi 1 kxi 1 pi 1 mx c pi ti xi given pi+1 tj xi+1 seek Time stepping
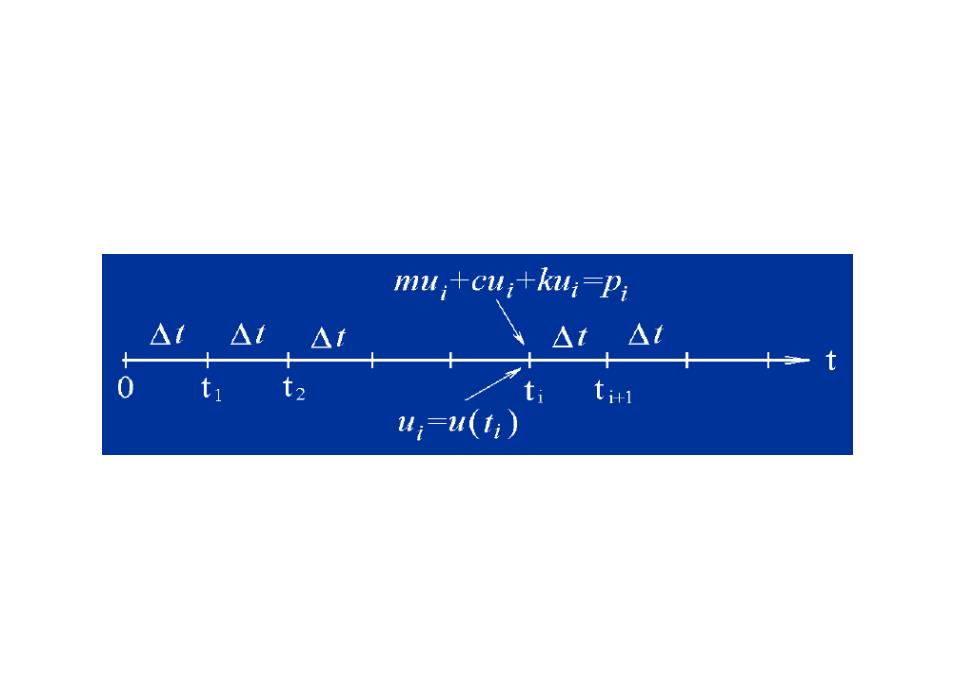
m4,+c4;+u,=P2 △ △t △ t计 u:-u(t1)

Duhamel's integral provides a general result for evaluating the response of a linear SDOF system to arbitrary force. When the force is simple,Duhamel's integral method is applicable. If the force is complicated function,evaluation of the integral requires numerical method and usually not efficient The exciting force exists only in digitized form,such as earthquake records. u()=p()(i-)d
• Duhamel’s integral provides a general result for evaluating the response of a linear SDOF system to arbitrary force. • When the force is simple, Duhamel’s integral method is applicable. • If the force is complicated function, evaluation of the integral requires numerical method and usually not efficient • The exciting force exists only in digitized form, such as earthquake records. 0 t u t p d h t

Accordingly,two basic approaches: Numerical evaluation of the Duhamel integral; Principle of Superposition->Linear system Direct integration of the equation of motion- step-by-step integration.Valid for both Linear and Non-linear systems->more commonly utilized. Response:at discrete time,usually with equal time internal
• Accordingly, two basic approaches: • Numerical evaluation of the Duhamel integral; Principle of Superposition → Linear system • Direct integration of the equation of motion – step-by-step integration. Valid for both Linear and Non-linear systems → more commonly utilized. • Response: at discrete time, usually with equal time internal