
G=是,=560x1072180 故 gπ/(18×10) (季澍) 1023(Ber,1973) 一跳伞员在3000m高处起跳。在降落伞张开之前她达 到一极限速度30m/s. (a)假定空气阻力正比于速度,使她到达这个速度约需 多久? (b)在达到这个速度时,她运行了多少距离? 在她的伞张开以后,她的速度降到3m/s。当她碰到地 面时,她弯曲膝部以减缓冲撞。 (c)为了经受一个不大于10g的减速度,她须将膝部弯 曲多少?假定她的膝部像弹簧一样具有正比于位移的阻力. ()空气阻力正比于速度的假定,是合理的么?用定性 的讨论说明这是否合理 解:(a)取铅垂向下的方向为坐标轴正向. 将运动微分方程 g00 积分得 v=g(1-ea) (1) 20

根据题目给定的条件要求出到达极限速度30/s的时 间,只能依据极限速度的定义和积分结果(1),得出时间 为无限大.但这似乎不是原题所要求的。 为了得出合适的结果,似乎应将问题(a)改换一下提 法:假定空气阻力正比于速度,为了使她到达的速度离极限 速度不大于百分之几(例如0.1%),最少需多少时间? 现取离极限速度不大于0,1%的情况计算所需时间。其 达到的速度 w=29.97=30(1-ea). 由此得 a=0.327. 代入上式,算得 t=21.12s. 即所需时间不小于21.12s. (b)将(1)再积分一次得 -(g+是e)儿“=5. (c)由于题中未给出降落伞张开情况下阻力和速度的关 系,故只好略去着地后的空气阻力。 根据机械能守恒应有 是x2=2m知+m0. 又 x=11mg, 所以 11 7mgx-mgx=之mw, 故 ×=0.102m. 之

()从以上计算看不出阻力正比于速度的假定有什么矛 盾,但实验证明,阻力与速度平方成正比的假定更接近实 际 (季澍) 1024(Col,1980) 赤道上方一同步卫星从一个1km的镜子发射波长为1 m的相干微波束,.以向地面站馈送能量. (a)这卫星的轨道高度是多少? (b)估计地面接收站所需的尺度。 解:(a)赤道上的同步卫星角速度和地球自转角速度相 同,从而 GMm m(R+)o2= (R+h) 故 6='/GM 1@ -R='/g √RaR-R~37000km. (b)由于光的衍射效应,地面接收器的尺度 1合·a=品×3700m=37如. (肖旭东) 1025(Col,1984) 质量为M的斜劈放在静摩擦系数为4的粗糙平面上· m1用弦线挂起并通过滑轮与在无摩擦的斜面上滑动的m:相 连.斜面的倾角是(图1.12)· (a)求当4非常大时m,和m,的加速度,以及弦的张力. (b)求使斜劈能保持静止的最小摩擦系数. 22
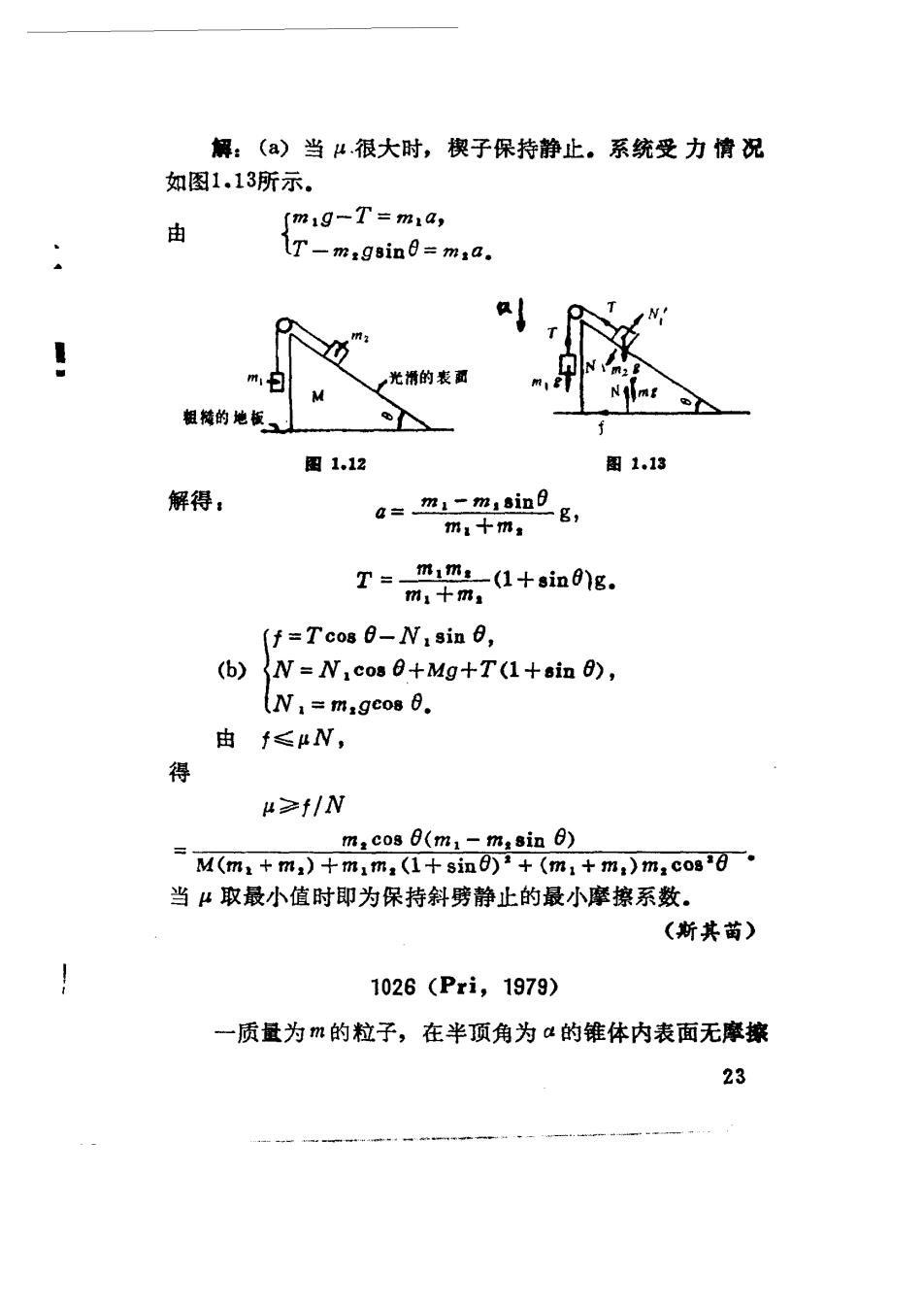
解:(a)当4很大时,楔子保持静止。系统受力情况 如图1.13所示. fmig-T=ma, IT-m:gsin0=m:a. m m 一光滑的表面 阻的地板、 图1.12 图1.13 解得: a=mming, m十m mm (1+sing. T=mm (f=Tcos 0-N,sin, (b)N=N,cos 0+Mg+T(1+sin 0), (N=m,gcos 6. 由f≤μN, 4≥f/N m:cos0(m1-m:sinf) =M(m.+m,)+m,m,(1+sin6)+(m,+m,)m,co8*6, 当4取最小值时即为保持斜劈静止的最小摩擦系数. (斯其苗) 1026(Pxi,1979) 一质量为m的粒子,在半顶角为“的锥体内表面无摩擦 23
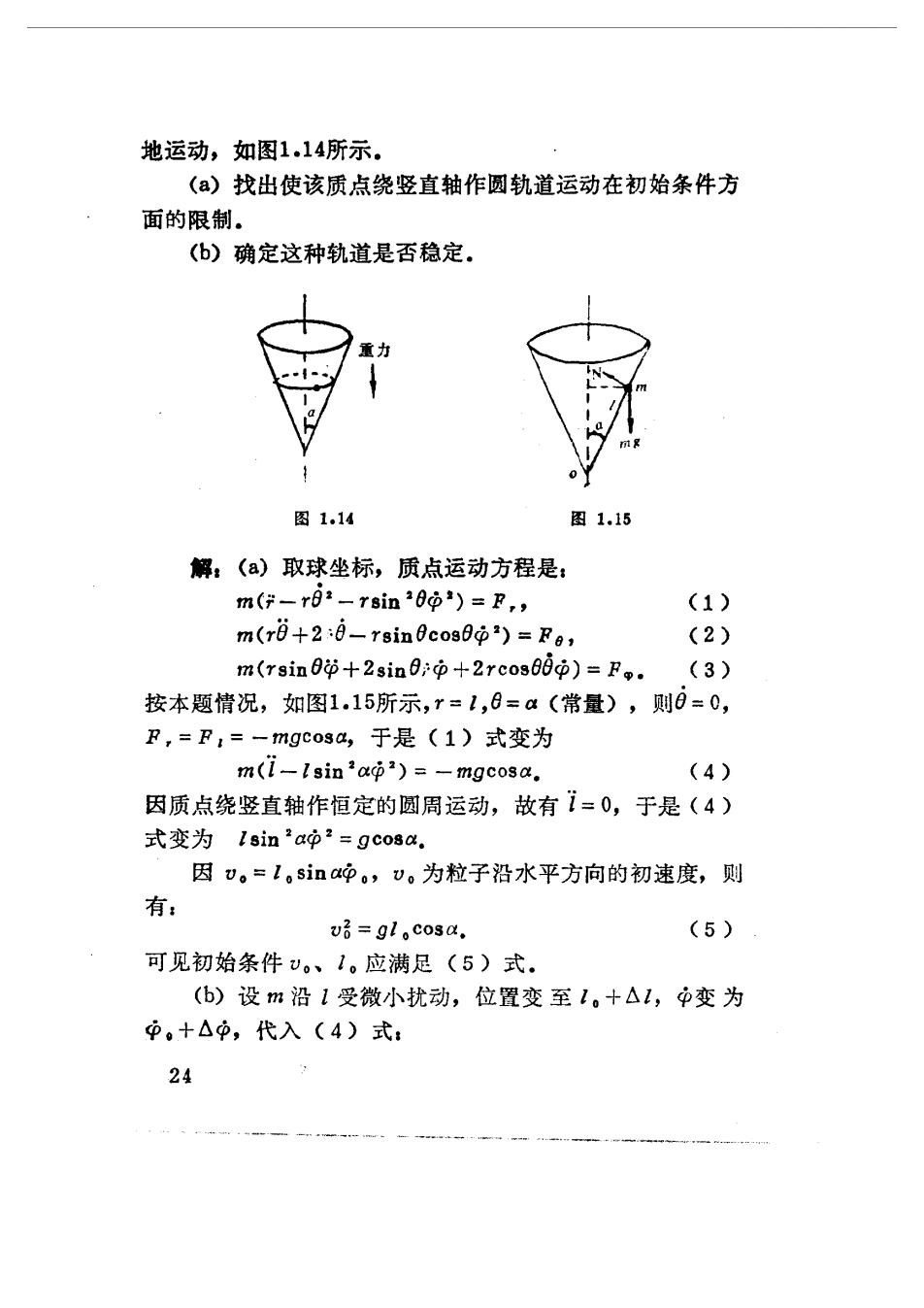
地运动,如图1.14所示。 ()找出使该质点绕竖直轴作圆轨道运动在初始条件方 面的限制。 (b)确定这种轨道是否稳定. 图1.14 图1.15 解:(a)取球坐标,质点运动方程是: m(:-r92-r8in20o)=F, (1) m(r0+2:0-rsin0cos0)=Fe, (2) m(rsin0p+2sin0中+2rcos的p)=F,. (3) 按本题情况,如图1.15所示,r=1,8=a(常量),则0=0, F,=F,=-mgco3a,于是(1)式变为 m(1-Isin'a)=-mgcosa. (4) 因质点绕竖直轴作恒定的圆周运动,故有1=0,于是(4) 式变为1sin2ap2=gco8a. 因。=1,sina冲。,v,为粒子沿水平方向的初速度,则 有: v3=gl,cosa. (5) 可见初始条件。、1。应满足(5)式. (b)设m沿1受微小扰动,位置变至1。十△1,中变为 中。+△中,代入(4)式: 24