
解:若记V。=60mph/h,则有V= 所以 普=~,,于是可知,卡车所受的阻力 和速度的关系为:F=0。八.其中m为卡车的质量,F 为阻力。要在同样的路上保持V'=30mphh的速度.则驱 动力应等于这种速度下的阻力F',而驱动功率P/=FV'. 所以 m B-200ft/4.5P. (乌千来) 1018(Wi8,1980) 一质量为m的小孩坐在一秋干上。秋千的质量可以忽 略,悬挂在长度为1的绳上。小孩的父亲 拉他的后背使绳子和铅直方向张开一弧度 角,然后以力F=mg沿圆周的弧线方向 推小孩直至绳子到达铅直位置并放开该秋 干,问孩子的父亲推秋干用了多少时间? 在本题的精度范围可以假定,对于日<1有 sin8≈6. 解:如图1.10,列出运动方程: ml0=-mg-mgsine,(0>0). 图1.10 所以 i+gsin9=-号. 15

令0=号, sin6≈6, 6+a0=-02. 方程的解是0=Acos@t+Bsin@t-l, 0=-Aosinot+Bocosot. 由初始条件定常数A和B, 当t=0时,0=1,日=0. 「A-1=1,故0=2 cos@t-1. 所以 B=0. 当0=0时,co8ot1=马 所以0,=号放,=合·号=晋√骨。此即为推秋干的 时间。 (马千来) 1019(Wis,1970) 一质量为m的质点受到两个力的作用:一个是中心力 f,=f().另一个是摩擦力f,=-λV(>0),其中V 是质点的速度.若该质点初始时对Y=0点的角动量是J。, 求以后时刻它的角动量。 解按极坐标列出方程: m(行-r82)=f(r)-λ, m(2:0+r)=-λr0. 第二式可以改写成号品(m0=-0, 16

若令 J=mr20, 则 -, 所以 J=J÷ (马千来) 1020'(CUS,1981) (a)一个球形物体以角频率o转动。如果仅仅有引力 园碍球的离心分解,那末这物体必须具有的最小密度是多 少?利用这一点估计巨蟹座中转速为每秒30转的脉冲星的最 小密度.(这是公元1054年在中国广泛地被观察到的一个 超新星爆发的遗迹!) (b)如果脉冲星的质量与太阳的质量相当(~2×10千 克或~3×10MEth,M:a:th为地球质量),这个脉冲星 的最大可能半径是多少? ·(©)若脉冲星的密度与核物质的密度相当时,它的半径 是多少? 解:(a)考虑球不分离的极限情况,赤道上的物体的向 心力正好是由引力提供。即 mo2/R=mRo2≤GmM/R2,或 M/R≥o2/G. 所以P≥ 6-3活-aE 3π×(30s-1) 3πG ~1.3×101kg/m3. (G为万有引力常数) 17
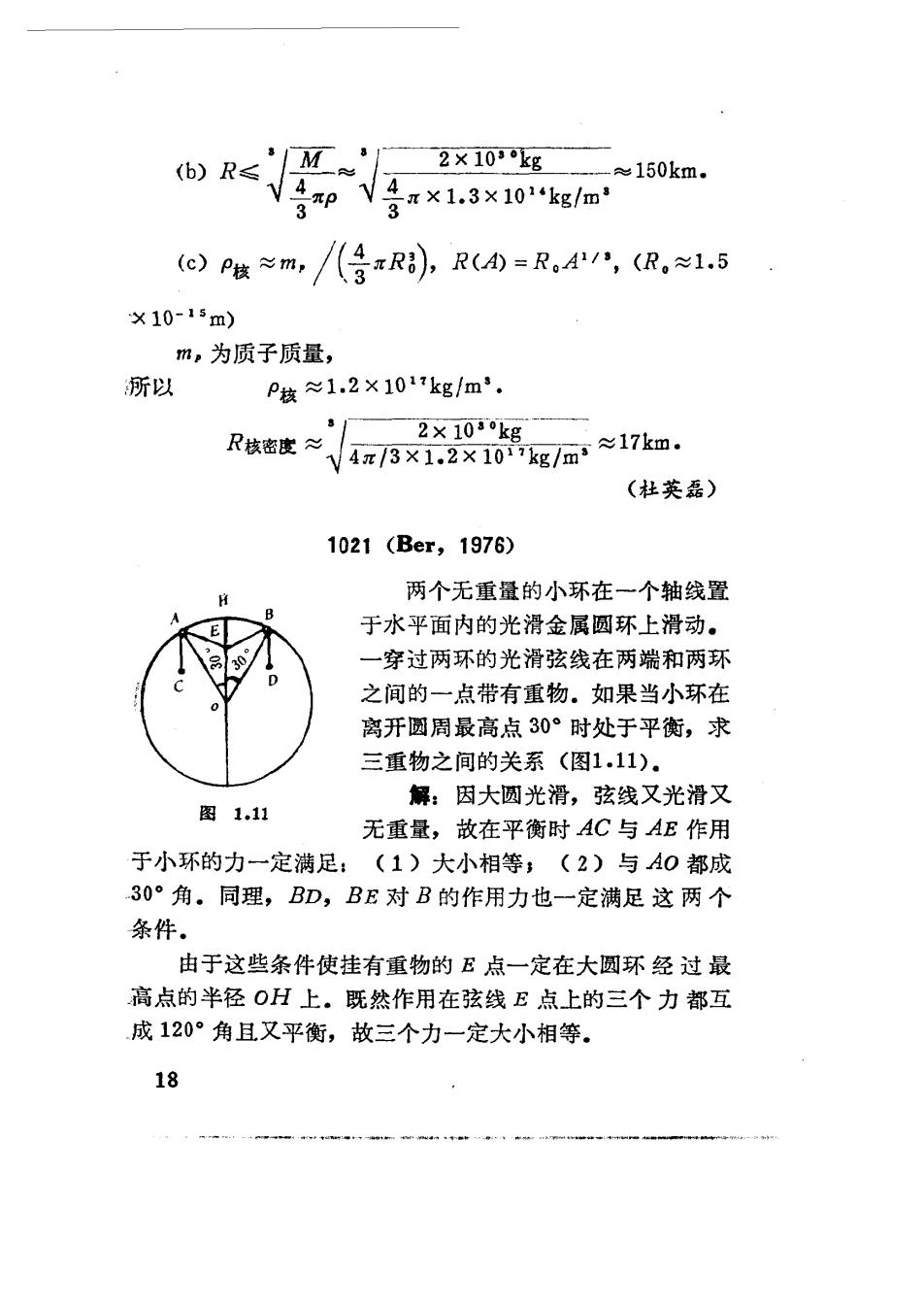
b)R≤M' 2×103kg -e150km, V含Vx1.3x10kg1 3 e)Pw≈m,八g✉R),R(0=R4,(R,≈1.5 ×10-15m) m,为质子质量, 所以 P技≈1.2×10kg/m. R核密度≈ 2×100kg 4π13×1.2×10kg/m≈17km. (杜英磊) 1021(Ber,1976) 两个无重量的小环在一个轴线置 于水平面内的光滑金属圆环上滑动。 一穿过两环的光滑弦线在两端和两环 之间的一点带有重物。如果当小环在 离开圆周最高点0°时处于平衡,求 三重物之间的关系(图1.11). 解:因大圆光滑,弦线又光滑又 图1.11 无重量,故在平衡时AC与AE作用 于小环的力一定满足:(1)大小相等,(2)与A0都成 30°角。同理,BD,BE对B的作用力也一定满足这两个 条件。 由于这些条件使挂有重物的E点一定在大圆环经过最 高点的半径OH上.既然作用在弦线E点上的三个力都互 成120°角且又平衡,故三个力一定大小相等. 中

所以,最后的结论是三重物的重量都相等。 (季澍) 1022(Ber,1976) 从以下近似数据计算地球和太阳平均密度的比率: 0=从地球上看太阳的角直径=1/2° 1=地球表面上纬度为1°的长度=100km, t=1年=3×1075, 9=10ms¥. 解:以r表示日、地距离,脚号e表示地球的量,脚 号s表示太阳的量,则 GM.M.=M.ro', r 2织=×0=g0rad, 多 7=720R 故 GM (70R,), 0-(0'×(3x7-八. Gmgy