同济大学：《结构动力学》课程教学资源（教案讲义）Lecture 06 Numerical Evaluation of Dynamic Response

Central Difference Method ·Finite difference(有限差分) Xi+l Xi X m+c+kxi pi Xi+1Xi-1 i=Xit1-Xi-1 2△t 2At x1=X+1-2X;+X包 △t2 △t△t mXi1-2xiXi-l+cXitl-Xi-1+kxi=Pi (At)2 2△t 人 (4t)22At =Pi-[m unknown

Central Difference Method Central Difference Method • Finite difference (有限差分） ii 1i1i 2 1ii1i pkx t2 x x c )t( x 2x x m                               2 1ii1i i 1i1i i t xx2x x t2 x x x   i 2 1i 2 i1i 2 x] )t( 2m k[x] t2 c )t( m [px] t2 c )t( m [              kˆ unknown Pi ˆ t x xi1  xi1 2t i x t t i 1 x  xi1 i xi kxi pi mx  c   xi

Central Difference Method (42 find need At t-0,given xo and Xo To find x1 we need xo and x-1 mi+cxi+kxi pi X0=0-c成0-kxg m x;=X+1-X1 2△t 80=X1-X 2△t 飞-X12;+x X0=1-2x0+X1 △t2 4t2 x-1=X0-△t仪0+ △t)2 0 2

Central Difference Method Central Difference Method At t=0, given x0 and x0  m p cx kx x 000 0                      2 101 0 11 0 t xx2x x t2 x x x   0 2 001 x 2 )t( xtxx         i 2 1i 2 i1i 2 x] )t( 2m k[x] t2 c )t( m [px] t2 c )t( m [              find need To find x1 we need x0 and x-1                   2 1ii1i i 1i1i i t xx2x x t2 x x x   i xi kxi pi mx  c  

Central Difference Method 。Summary Given m,c,k,p,xo and Xo Xo=Po-cXo-kxo m X1=X0A0+a2 0 k=m (4t)22At a=- m (4t)22At b=k-- 2m (4)2 For step i Pi=Pi-a.xi-1-b.xi XH-段 i=Xi+1-Xi-1 =Xil-2xi+xi=1 2△t 42 p

Central Difference Method Central Difference Method • Summary Given m, c, k, p, and x0 x0  m p cx kx x 000 0      0 2 001 x 2 )t( xtxx         t2 c )t( m kˆ 2     t2 c )t( m a 2     2 )t( 2m kb    For step i i i i 1 i pˆ  p  a  x  b  x  kˆ pˆ x i 1i  2 1ii1i i 1i1i i t x 2x x x t2 x x x             

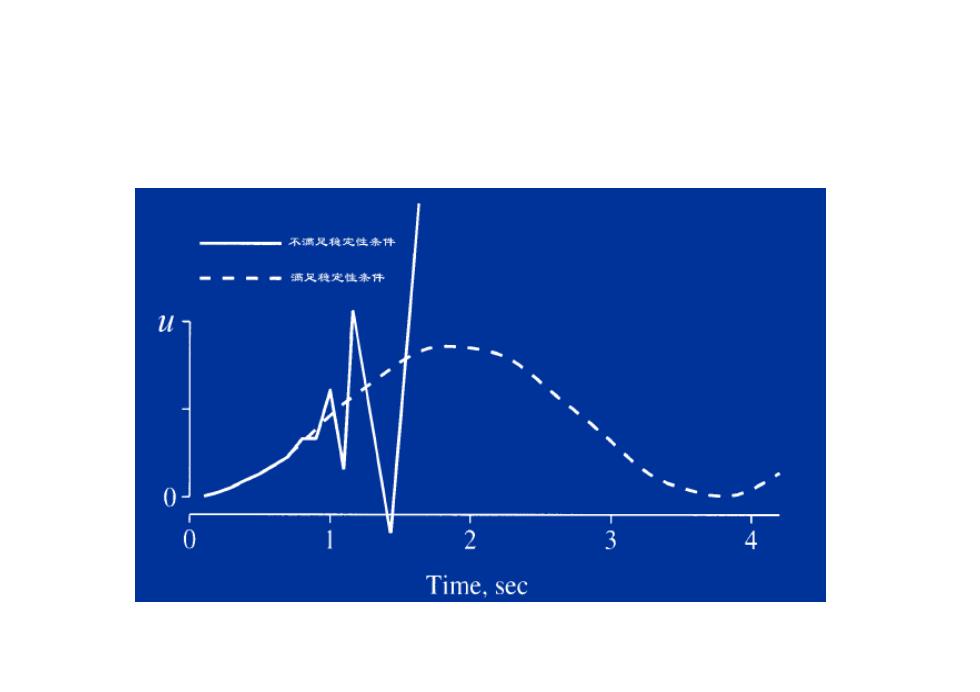
Statibility condition When the time interval satifies the statibility condition the calculation(the response u(t))will be finite (within certain boundaries) △t.1 T 元 人 c U)22At t1=Pi-[m (4t)22At k-1-k-2mK (△t)2

• When the time interval satifies the statibility condition the calculation (the response u(t)) will be finite (within certain boundaries)  1   Tn t Statibility condition i 2 1i 2 i1i 2 x] )t( 2m k[x] t2 c )t( m [px] t2 c )t( m [             

0 2 4 Time,sec