
当单口网络中包含有独立电源和受控源时,计算平均 功率的式(11~3)仍然适用,但此时的电压与电流的相位差 p可能在+0到+270°之间变化,功率因数c0s在0到-1之间 变化,导致平均功率为负值,这意味着单口网络向外提供 能量。 值得注意的是在用U1cos心计算单▣网络吸收的平均功 率时,一定要采用电压电流的关联参考方向,否则会影响 相位差的数值,从而影响到功率因数cosol以及平均功率的 正负
当单口网络中包含有独立电源和受控源时,计算平均 功率的式(11-3)仍然适用,但此时的电压与电流的相位差 可能在+90到+270之间变化,功率因数cos在0到-1之间 变化,导致平均功率为负值,这意味着单口网络向外提供 能量。 值得注意的是在用UIcos计算单口网络吸收的平均功 率时,一定要采用电压电流的关联参考方向,否则会影响 相位差的数值,从而影响到功率因数cos以及平均功率的 正负

二、功率因数 从式(11-3)可见,在单口网络电压电流有效值的乘积 U一定的情况下,单口网络吸收的平均功率P与cos的大 小密切相关,c0s表示功率的利用程度,称为功率因数, 记为入,它与P和U的关系为 P A=coso= (11-7) vl 功率因数c0sp之值与单口网络电压与电流间的相位差 密切相关,故称py,-必为功率因数角
= cos = (11− 7) UI P 功率因数cos 之值与单口网络电压与电流间的相位差 密切相关,故称=u -i为功率因数角。 二、功率因数 从式(11-3)可见,在单口网络电压电流有效值的乘积 UI一定的情况下,单口网络吸收的平均功率P与cos的大 小密切相关,cos表示功率的利用程度,称为功率因数, 记为,它与P和UI的关系为

当单口网络呈现纯电阻时,功率因数角为零以及功率 因数c0s1,功率利用程度最高。当单口网络等效为一个 电阻与电感或电容连接时,即单口呈现电感性或电容性时, 功率因数角o=0~土90以及功率因数cos<1,以致于P<UI。 为了提高电能的利用效率,电力部门采用各种措施力求提 高功率因数
当单口网络呈现纯电阻时,功率因数角为零以及功率 因数cos=1,功率利用程度最高。当单口网络等效为一个 电阻与电感或电容连接时,即单口呈现电感性或电容性时, 功率因数角=090以及功率因数cos<1,以致于P<UI。 为了提高电能的利用效率,电力部门采用各种措施力求提 高功率因数
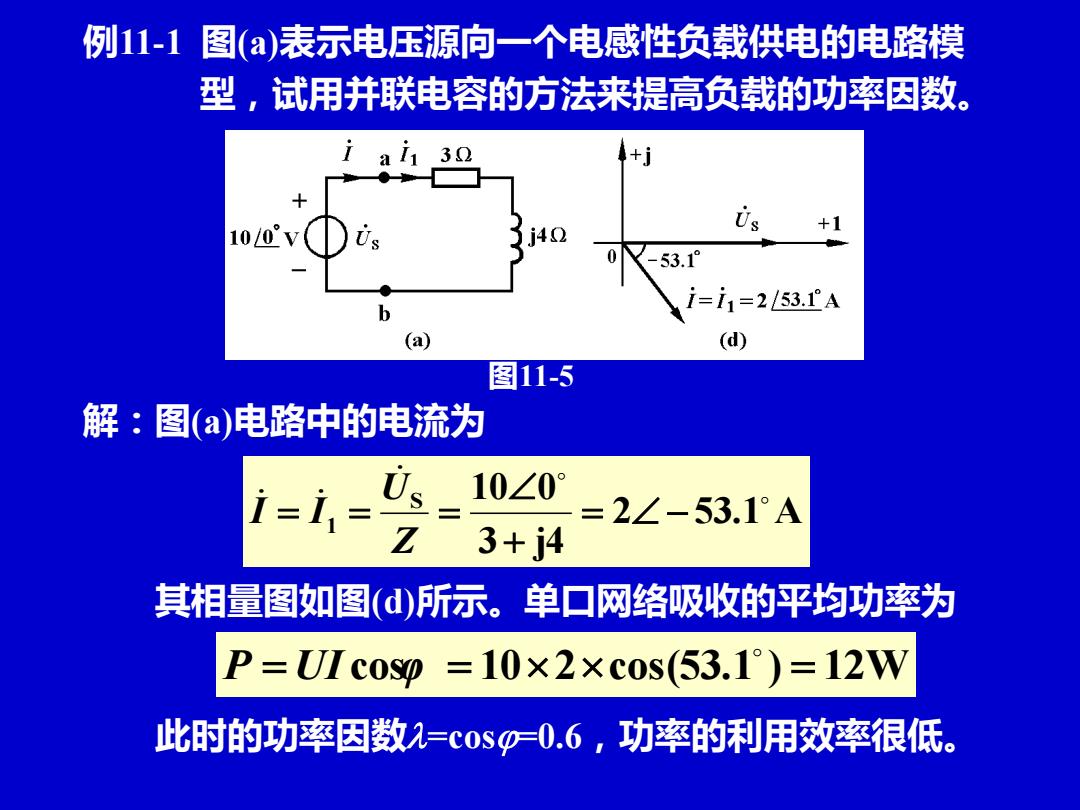
例11-1图(a)表示电压源向一个电感性负载供电的电路模 型,试用并联电容的方法来提高负载的功率因数。 32 100 Us +1 -53.1° i=i1=253.1A (d) 图11-5 解:图(a)电路中的电流为 i-1 Us 10∠0° =2∠-53.1°A Z 3+j4 其相量图如图()所示。单口网络吸收的平均功率为 P=UIc0s=10×2×c0s(53.1)=12W 此时的功率因数2=cos-0.6,功率的利用效率很低
例11-1 图(a)表示电压源向一个电感性负载供电的电路模 型,试用并联电容的方法来提高负载的功率因数。 解:图(a)电路中的电流为 2 53.1 A 3 j4 S 10 0 1 = − + = = = Z U I I 其相量图如图(d)所示。单口网络吸收的平均功率为 P = UI cosφ = 102cos(53.1 ) = 12W 此时的功率因数=cos=0.6,功率的利用效率很低。 图11-5
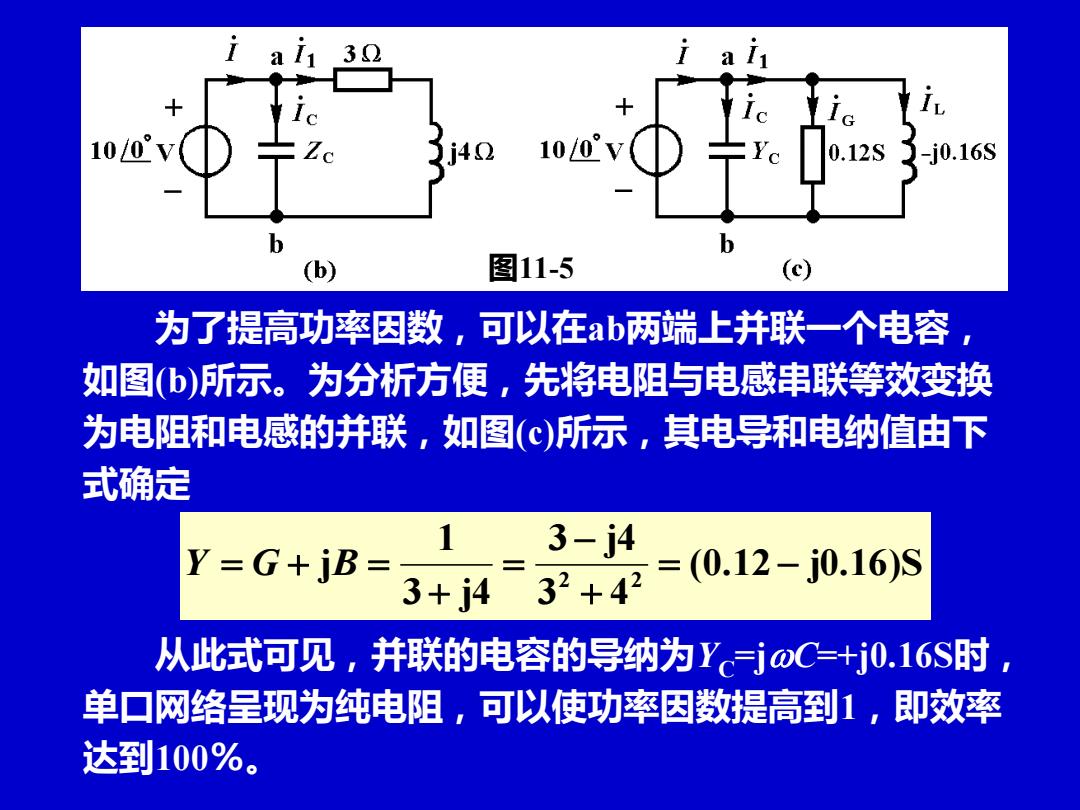
302 1 10/0 j42 100 0.12S3-j0.16S b (b) 图11-5 (c) 为了提高功率因数,可以在ab两端上并联一个电容 如图(b)所示。为分析方便,先将电阻与电感串联等效变换 为电阻和电感的并联,如图(©)所示,其电导和电纳值由下 式确定 3-j4 Y=G+jB = 3+j4 32+42 =(0.12-i0.16)S 从此式可见,并联的电容的导纳为Yc=joC=+j0.16S时, 单口网络呈现为纯电阻,可以使功率因数提高到1,即效率 达到100%
为了提高功率因数,可以在ab两端上并联一个电容, 如图(b)所示。为分析方便,先将电阻与电感串联等效变换 为电阻和电感的并联,如图(c)所示,其电导和电纳值由下 式确定 (0.12 j0.16)S 3 4 3 j4 3 j4 1 j 2 2 = − + − = + Y = G + B = 从此式可见,并联的电容的导纳为YC=jC=+j0.16S时, 单口网络呈现为纯电阻,可以使功率因数提高到1,即效率 达到100%。 图11-5