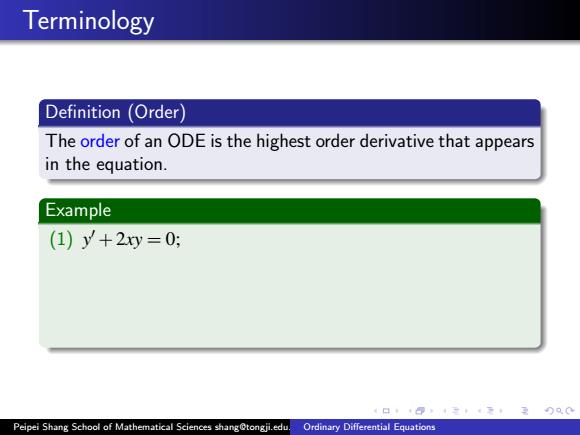
Terminology Definition (Order) The order of an ODE is the highest order derivative that appears in the equation. Example (1)y+2y=0: 4日10y4至,1无2000 Peipei Shang School of Mathematical Sciences shang tongji.edu.Ordinary Differential Equations
Terminology Definition (Order) The order of an ODE is the highest order derivative that appears in the equation. Example (1) y 0 +2xy = 0; ( first order) (2) xy 00 +y 0 = x 2 ; ( second order) (3) y 000 −x(y 0 ) 3 +y = 0; ( third order) (4) d 2 y dt 2 +y = cos 2t; (second order) Peipei Shang School of Mathematical Sciences shang@tongji.edu.cn Ordinary Differential Equations

Terminology Definition (Order) The order of an ODE is the highest order derivative that appears in the equation. Example (1)y+2xy=0;first order) 4日10y4至,1无2000 Peipei Shang School of Mathematical Sciences shang tongji.edu.Ordinary Differential Equations
Terminology Definition (Order) The order of an ODE is the highest order derivative that appears in the equation. Example (1) y 0 +2xy = 0; ( first order) (2) xy 00 +y 0 = x 2 ; ( second order) (3) y 000 −x(y 0 ) 3 +y = 0; ( third order) (4) d 2 y dt 2 +y = cos 2t; (second order) Peipei Shang School of Mathematical Sciences shang@tongji.edu.cn Ordinary Differential Equations

Terminology Definition (Order) The order of an ODE is the highest order derivative that appears in the equation. Example (1)y+2xy=0;first order) (2)”+y=x2; 4日10y4至,1无2000 Peipei Shang School of Mathematical Sciences shang tongji.edu.Ordinary Differential Equations
Terminology Definition (Order) The order of an ODE is the highest order derivative that appears in the equation. Example (1) y 0 +2xy = 0; ( first order) (2) xy00 +y 0 = x 2 ; ( second order) (3) y 000 −x(y 0 ) 3 +y = 0; ( third order) (4) d 2 y dt 2 +y = cos 2t; (second order) Peipei Shang School of Mathematical Sciences shang@tongji.edu.cn Ordinary Differential Equations

Terminology Definition (Order) The order of an ODE is the highest order derivative that appears in the equation. Example (1)y+2xy=0;first order) (2)xy+y=x2;second order) 4日10y4至,1无2000 Peipei Shang School of Mathematical Sciences shang@tongji.edu.Ordinary Differential Equations
Terminology Definition (Order) The order of an ODE is the highest order derivative that appears in the equation. Example (1) y 0 +2xy = 0; ( first order) (2) xy00 +y 0 = x 2 ; ( second order) (3) y 000 −x(y 0 ) 3 +y = 0; ( third order) (4) d 2 y dt 2 +y = cos 2t; (second order) Peipei Shang School of Mathematical Sciences shang@tongji.edu.cn Ordinary Differential Equations

Terminology Definition (Order) The order of an ODE is the highest order derivative that appears in the equation. Example (1)y+2xy=0;first order) (2)xy+y=x2;second order) (3)y"-xy)3+y=0: 4日10y4至,1无2000 Peipei Shang School of Mathematical Sciences shang tongji.edu.Ordinary Differential Equations
Terminology Definition (Order) The order of an ODE is the highest order derivative that appears in the equation. Example (1) y 0 +2xy = 0; ( first order) (2) xy00 +y 0 = x 2 ; ( second order) (3) y 000 −x(y 0 ) 3 +y = 0; ( third order) (4) d 2 y dt 2 +y = cos 2t; (second order) Peipei Shang School of Mathematical Sciences shang@tongji.edu.cn Ordinary Differential Equations