
Example (Heat equation) The temperature u=u(x,t)of a long thin uniform rod satisfies du 2u where k is the thermal diffusivity of the rod. Definition (PDE) Partial differential equations:differential equations that involve an unknown function of more than one independent variables, together with partial derivatives of the function. 4口14①y至,元2000 Peipei Shang School of Mathematical Sciences shang@tongji.edu.Ordinary Differential Equations
Example (Heat equation) The temperature u = u(x,t) of a long thin uniform rod satisfies ∂u ∂ t = k ∂ 2u ∂ x 2 , where k is the thermal diffusivity of the rod. Definition (PDE) Partial differential equations: differential equations that involve an unknown function of more than one independent variables, together with partial derivatives of the function. Peipei Shang School of Mathematical Sciences shang@tongji.edu.cn Ordinary Differential Equations
Example (1)y+29y=0: 4日10y4至,1无2000 Peipei Shang School of Mathematical Sciences shang tongji.edu.Ordinary Differential Equations
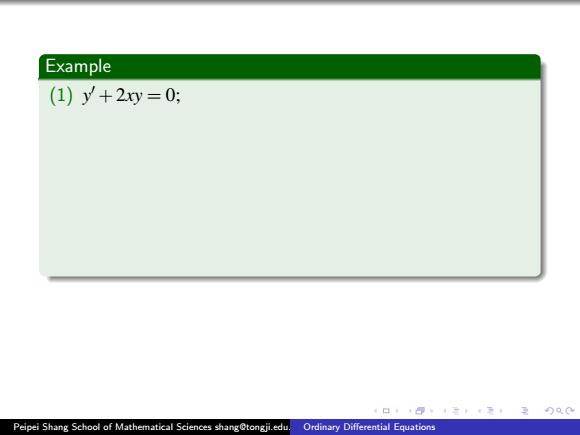
Example (1) y 0 +2xy = 0; (ODE) (2) xy 00 +y 0 = x 2 ; (ODE) (3) y 000 −x(y 0 ) 3 +y = 0; (ODE) (4) d 2 y dt 2 +y = cos 2t; (ODE) (5) ∂ 2T ∂ x 2 + ∂ 2T ∂ y 2 + ∂ 2T ∂ z 2 = 0; (PDE) (6) ∂ 2u ∂ x 2 = ∂u ∂ t +u. (PDE) Remark There are multiple criteria to classify ODEs. Peipei Shang School of Mathematical Sciences shang@tongji.edu.cn Ordinary Differential Equations

Example (1)y+2y=0:(ODE) 4日10y4至,1无2000 Peipei Shang School of Mathematical Sciences shang@tongji.edu.Ordinary Differential Equations
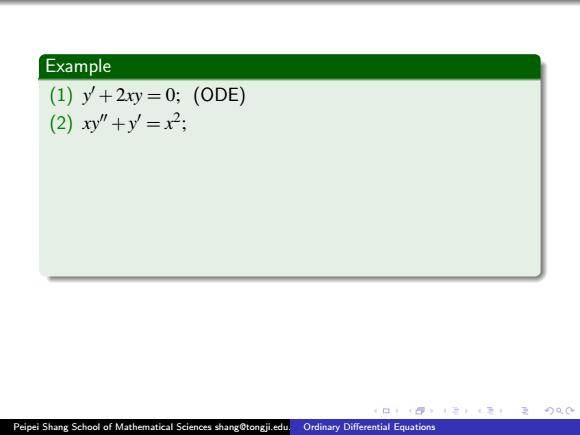
Example (1) y 0 +2xy = 0; (ODE) (2) xy 00 +y 0 = x 2 ; (ODE) (3) y 000 −x(y 0 ) 3 +y = 0; (ODE) (4) d 2 y dt 2 +y = cos 2t; (ODE) (5) ∂ 2T ∂ x 2 + ∂ 2T ∂ y 2 + ∂ 2T ∂ z 2 = 0; (PDE) (6) ∂ 2u ∂ x 2 = ∂u ∂ t +u. (PDE) Remark There are multiple criteria to classify ODEs. Peipei Shang School of Mathematical Sciences shang@tongji.edu.cn Ordinary Differential Equations
Example (1)y+2y=0;(ODE) (2)x”+y=x2; 4日10y至,1元3000 Peipei Shang School of Mathematical Sciences shang tongji.edu.Ordinary Differential Equations
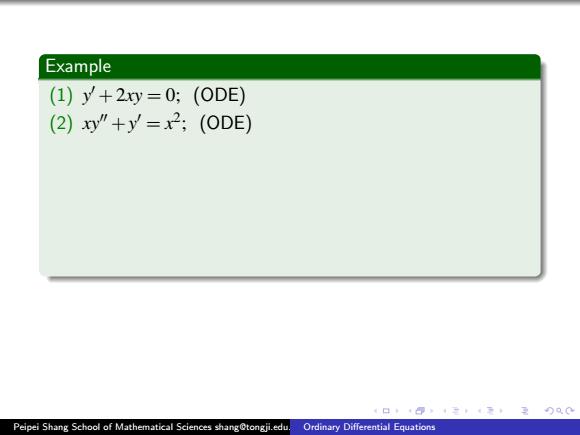
Example (1) y 0 +2xy = 0; (ODE) (2) xy00 +y 0 = x 2 ; (ODE) (3) y 000 −x(y 0 ) 3 +y = 0; (ODE) (4) d 2 y dt 2 +y = cos 2t; (ODE) (5) ∂ 2T ∂ x 2 + ∂ 2T ∂ y 2 + ∂ 2T ∂ z 2 = 0; (PDE) (6) ∂ 2u ∂ x 2 = ∂u ∂ t +u. (PDE) Remark There are multiple criteria to classify ODEs. Peipei Shang School of Mathematical Sciences shang@tongji.edu.cn Ordinary Differential Equations
Example (1)y+2y=0; (ODE) (2)x”+y=x2;(ODE) 4日10y至,1元3000 Peipei Shang School of Mathematical Sciences shang tongji.edu.Ordinary Differential Equations
Example (1) y 0 +2xy = 0; (ODE) (2) xy00 +y 0 = x 2 ; (ODE) (3) y 000 −x(y 0 ) 3 +y = 0; (ODE) (4) d 2 y dt 2 +y = cos 2t; (ODE) (5) ∂ 2T ∂ x 2 + ∂ 2T ∂ y 2 + ∂ 2T ∂ z 2 = 0; (PDE) (6) ∂ 2u ∂ x 2 = ∂u ∂ t +u. (PDE) Remark There are multiple criteria to classify ODEs. Peipei Shang School of Mathematical Sciences shang@tongji.edu.cn Ordinary Differential Equations