山东理工大学：《电工学（电子技术）》课程教学资源（PPT课件讲稿）第七章 门电路和组合逻辑电路

二.逻辑代数的基本运算公式 1.常量与变量的关系 自等律 A+0=A A.1=A 0-1律 A+1=1 A.0=0 重叠律 A十A=A A·A=A 还原律 A=A 互补律A+A=1A.A=0 2.逻辑代数的基本运算法则 交换律A+B=B+A A·B=B·A

1. 常量与变量的关系 二. 逻辑代数的基本运算公式 2. 逻辑代数的基本运算法则 自等律 A+ 0 = A A1 = A 0-1律 A+1 = 1 A0 = 0 重叠律 A+ A = A A A = A 还原律 A = A 互补律 A+ A = 1 A A = 0 交换律A+ B = B + A AB = B A

结合律 (A+B)+C=A+(B+C) (AB)C=A·(B.C) 普通代数 分配律A·(B+C)=A·B+A·C还适用 A+(B.C)=(A+B)(A+C) 证：(A+B)(A+C) =A·A+AC+B.A+B.CAA=A =4+A(C+B)+BC A+1=1 =4(1+C+B)+BC =A+BC

普通代数 不适用！ 证 : = A A + AC + B A + BC 结合律 ( A + B ) + C = A + ( B + C ) ( AB )C = A( BC ) 分配律 A( B + C ) = AB + AC A + ( BC ) = ( A + B )( A + C ) ( A + B )( A + C ) = A + A ( C + B ) + BC = A(1 + C + B ) + BC = A + BC A+1=1 A A=A

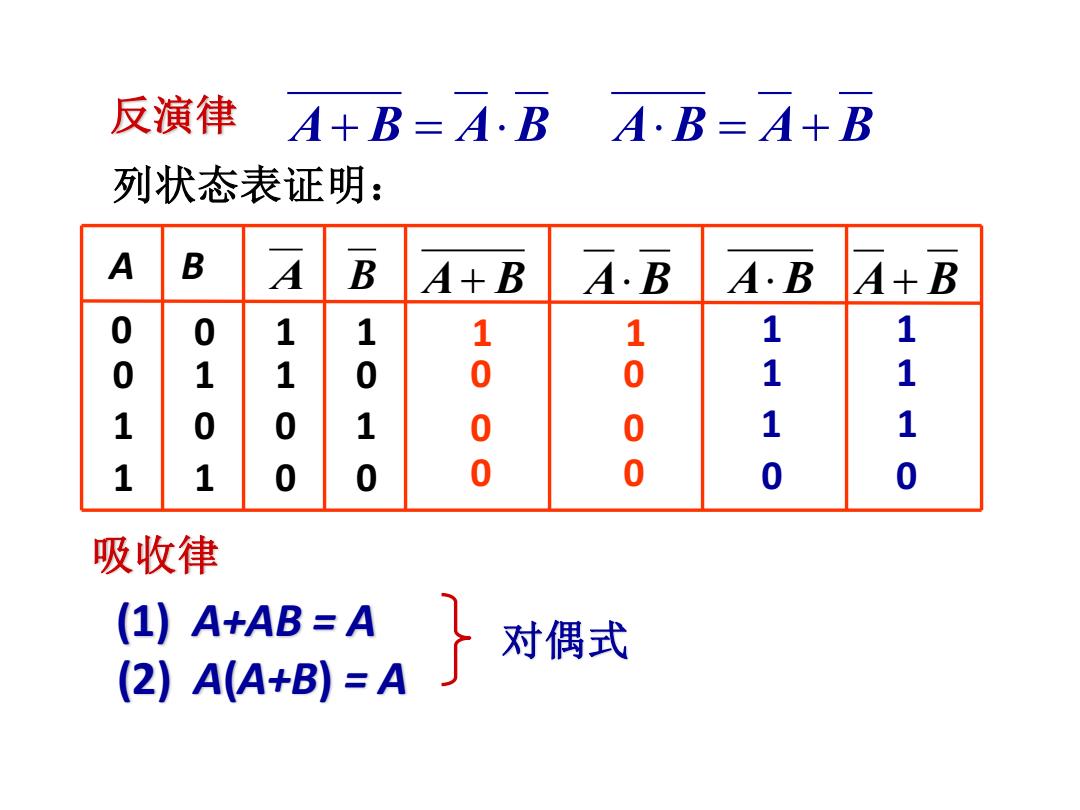
反演律 A+B=A.B A·B=A+B 列状态表证明： A B A B A+B A.B A+B 0 0 1 1 1 1 1 1 0 1 1 0 0 0 1 1 1 0 0 1 0 0 1 1 1 1 0 0 0 0 0 0 吸收律 (1)A+AB=A 对偶式 (2)A(A+B)=A

1 1 0 0 1 1 1 1 1 1 0 0 反演律 A+ B = AB AB = A+ B 列状态表证明： A B 0 0 0 1 1 0 1 1 1 1 1 0 0 1 0 0 A B A+ B AB AB A+ B 0 0 0 0 吸收律 (1) A+AB = A (2) A(A+B) = A 对偶式

《1 (4)A(A+B)=AB 对偶式 证明：☑rAB①+AB+AB A+AB=A =A+B(A+A)=A+B 酒d 对偶式

证明 ： = A + B ( A + A ) = A + B A + AB = A + AB + AB A+AB = A A ( A + B ) = AB （ 3 ） A + ( AB ) = A + B （ 4 ） 对偶式 ( A + B)( A + B ) = A （ 5 ） AB + ( A B ) = A （ 6 ） 对偶式

三. 逻辑函数的表示及其化简 1.逻辑函数的概念：逻辑式中，输出变量是输入变 量的逻辑函数。表示：F=(A,B,C…) 特点：表示输出与输入间逻辑关系 包括三种基本运算 变量取值只能为“0”、’1” 逻辑状态表 2.表示方法 逻辑式F=(A,B,C…) 逻辑图 卡诺图 3、最小项概念及表示法P117

2.表示方法 逻辑式 F=(A,B,C…) 逻辑状态表 逻辑图 卡诺图 1.逻辑函数的概念：逻辑式中，输出变量是输入变 量的逻辑函数。表示：F=(A,B,C…) 三. 逻辑函数的表示及其化简 特点：表示输出与输入间逻辑关系 包括三种基本运算 变量取值只能为“0”、’1” 3、最小项 概念 及表示法 P117