工程流体力学 Engineering Fluld Mechanics 7.1微弱压强波的一维传播】 声速马赫数 一、微弱压强波的一维传播 du dv 为了推求微弱压强波在圆 P2P2T2 PIP T 管中的传播速度c,选用与 777777777777777777777777 77777777777777777777777T 微弱压强波一起运动的相 P2 对坐标系作为参考坐标系 p P2 P2 P2 c-dv Pi T2 T 77777777 77777777777 dv du (a) (b) 压缩波 膨胀波
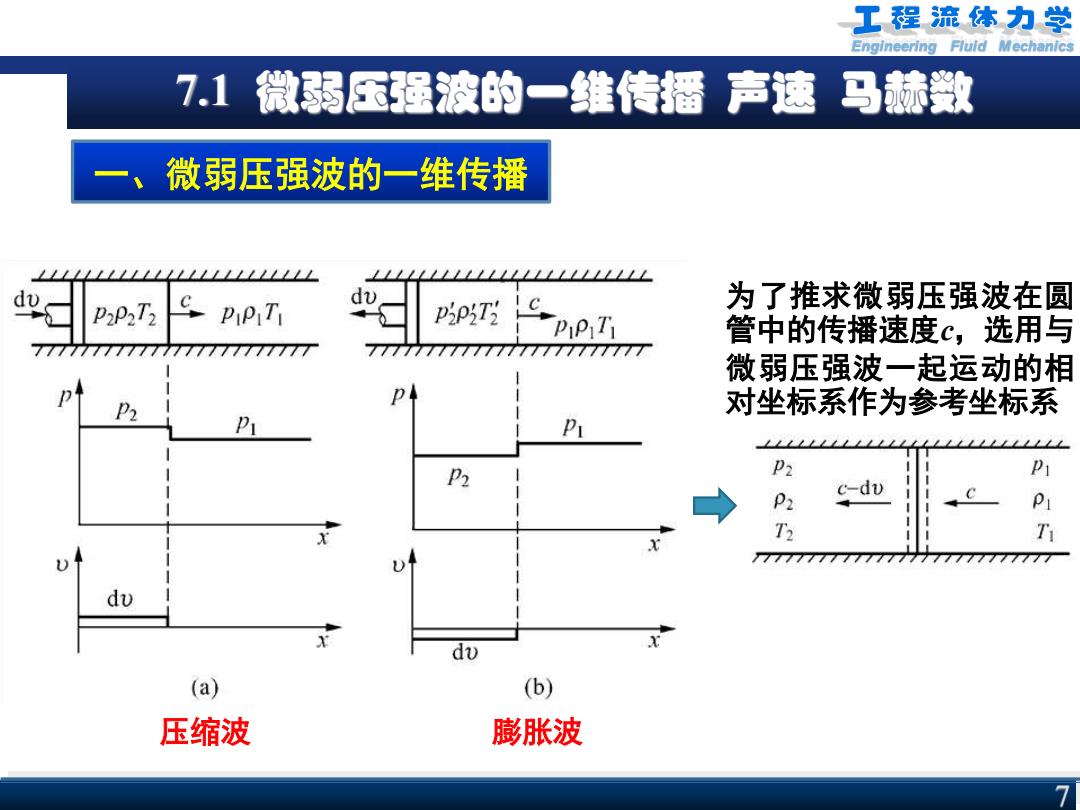
Engineering Fluid Mechanics 7.1 微弱压强波的一维传播 声速 马赫数 7 一、微弱压强波的一维传播 为了推求微弱压强波在圆 管中的传播速度c,选用与 微弱压强波一起运动的相 对坐标系作为参考坐标系 压缩波 膨胀波

工程流体力学 Engineering Fluld Mechanics 7.1 微弱压强波的一维传播声速马赫数 P2 P P2 c-dv P1 T T 777 777777 取图中虚线及其间管壁为控制体,则由连续方程得 (p:+dp)(c-dv)A-pcA=0 略去二阶微量,得 cdp-pdv 由动量方程得 PiCAl(c-dv)-c]=[p1-(p+dp)1A 即 Picdv-dp -1/2 1/2 Prcd-ip dp 8
Engineering Fluid Mechanics 7.1 微弱压强波的一维传播 声速 马赫数 8 取图中虚线及其间管壁为控制体,则由连续方程得 (1+d) (c−dv)A−1cA= 0 略去二阶微量,得 cd=1dv 由动量方程得 1cA[(c−dv)−c] = [p1−( p1+dp)]A 即 1cdv=dp 1/2 1/2 d d d d s s p c p − = = cd=1dv 1cdv=dp

工程流体力学 Engineering Fluld Mechanics 7.1微弱压强波的一维传播 声速马赫数 二、声速 微弱压强波传播速度 对于流体,当有微弱的压强扰动时,流体的体积模量: K=- dp dp dV/V 1/2 1/2 do C-(K/p)iR2 对于完全气体,由等熵过程关系式plp=C以及状态方程p=pRT,得 c=(r plp)=(YRT)2 对于空气,y=1.4,R=287.1J/kgK),得空气中的声速 c=20.05T2
Engineering Fluid Mechanics 7.1 微弱压强波的一维传播 声速 马赫数 9 二、声速 微弱压强波传播速度 对于流体,当有微弱的压强扰动时,流体的体积模量: 1 d d d / d p K V V p − = − = c=(K/) 1/2 对于完全气体,由等熵过程关系式 p/ =C 以及状态方程p=RT,得 1/ 2 1/ 2 c p RT = = ( / ) ( ) 对于空气, =1.4,R=287.1J/(kg·K),得空气中的声速 c = 20.05T 1/2 1/2 1/2 d d d d s s p c p − = =

工程流体力学 Engineering Fluld Mechanics 7.1 微弱压强波的一维传播声速马赫数 1/2 1/2 综上所述,可以看出: C= dp (1)流体中的声速是状态参数的函数。 (2)在相同温度下,不同介质中有不同的声速。 (3)在同一气体中,声速随着气体温度的升高而增 高,并与气体热力学温度的平方根成比例。 10
Engineering Fluid Mechanics 7.1 微弱压强波的一维传播 声速 马赫数 10 综上所述,可以看出: (1)流体中的声速是状态参数的函数。 (2)在相同温度下,不同介质中有不同的声速。 (3)在同一气体中,声速随着气体温度的升高而增 高,并与气体热力学温度的平方根成比例。 1/2 1/2 d d d d s s p c p − = =