
3、逻辑代数的基本公式和常用公式 基本公式 0-1律:0A=0,0+A=A,1·A=A,1+A=1 重叠律:A·A=A,A+A=A,A·A=0,A+A=1 交换律:AB=BA, A+B-B+A 结合律:A(BC)=(AB)·C,A+(B+C)=(A+B)+C 分配律:A·B+C)=AB+A·C A+B.C=(A+B)(A+C) 反演律: AB=A+B A+B=A·B 还原律: A=A,1=0, 0=1
基本公式 还原律: A=A , 1=0 , 0=1 0—1律: 0·A=0, 0+A=A, 1 · A=A, 1+A=1 重叠律: A ·A=A , A+A=A , A·A=0 , A+A=1 交换律:A·B=B·A , A+B=B+A 结合律:A·(B·C)=(A·B) ·C , A+(B+C)=(A+B)+C 分配律:A· (B+C)=A·B+A·C A+B·C=(A+B) ·(A+C) 反演律: A·B=A+B , A+B = A·B 3、逻辑代数的基本公式和常用公式

常用公式 A+A·B=A A+AB=A+B AB+AB=A A·(A+B)=A AB+AC+BC=AB+A·C A·B+AC+BCD=A·B+A·C A·AB=A·B AAB-A
A+A·B=A A+A·B=A+B A·B+A·B=A A·(A+B)=A A·B+A·C+B·C=A·B+A·C A·B+A·C+BCD=A·B+A·C A·A·B=A·B A·AB=A 常用公式

4、逻辑函数的表示方法 1)逻辑真值表 2)逻辑函数式 相互转换 3)逻辑图 4)卡诺图
1)逻辑真值表 2)逻辑函数式 3)逻辑图 4)卡诺图 相互转换 4、逻辑函数的表示方法
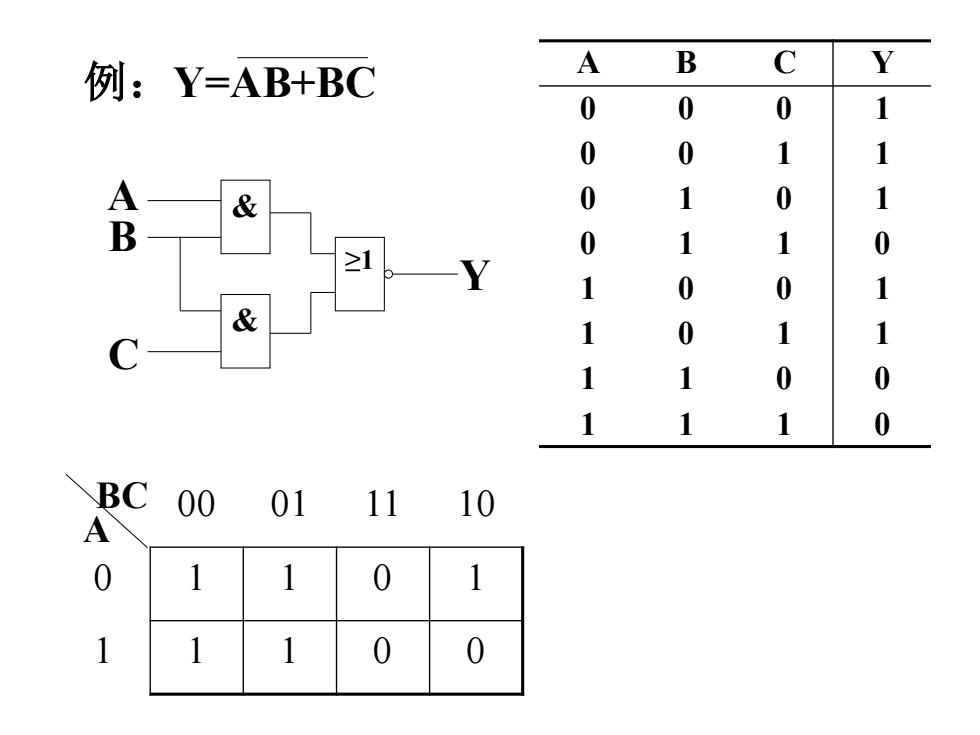
例:Y=AB+BC A B Y 0 0 0 1 0 0 1 1 A & 0 1 0 1 B 0 1 1 0 Y 1 0 0 1 & 1 0 1 1 C 1 1 0 0 1 1 1 0 BC 00 01 11 10 A 0 1 1 0 1 1 1 1 0 0
例:Y=AB+BC && ≥1 ABC Y A B C Y 0 0 0 1 0 0 1 1 0 1 0 1 0 1 1 0 1 0 0 1 1 0 1 1 1 1 0 0 1 1 1 0 00 01 11 10 0 1 1 0 1 1 1 1 0 0 A BC
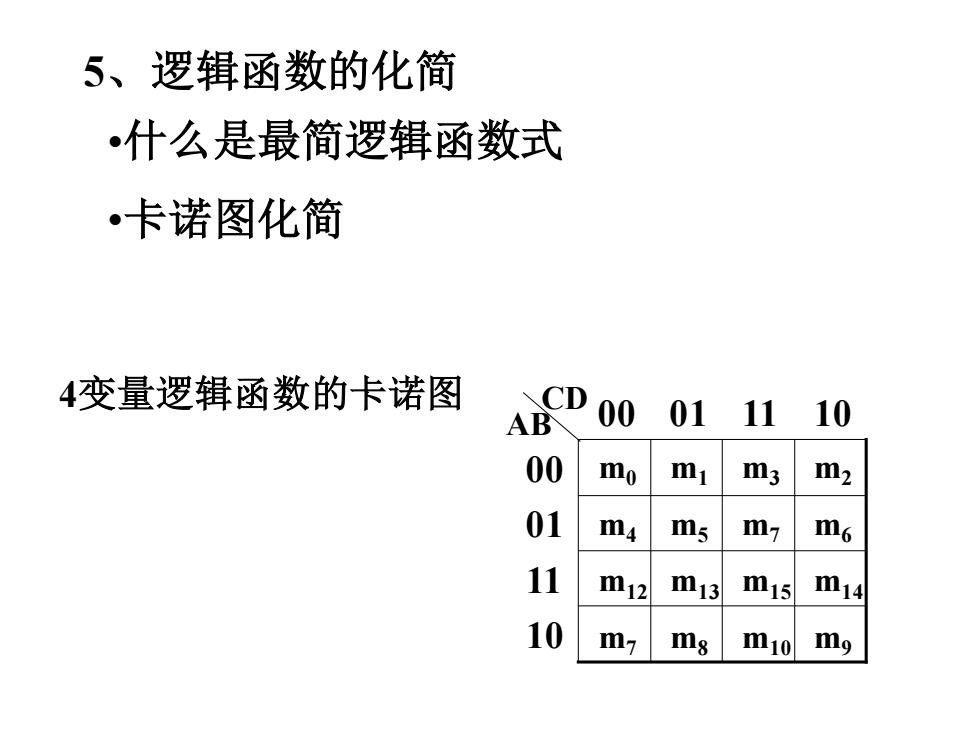
5、逻辑函数的化简 •什么是最简逻辑函数式 ●卡诺图化简 4变量逻辑函数的卡诺图 CD 00 AB 0111 10 00 mo mi m3 m2 01 m m5 m7 m6 11 m12 m13 m15 m14 10 ms mi0m9
•什么是最简逻辑函数式 •卡诺图化简 4变量逻辑函数的卡诺图 10 11 01 00 AB 00 01 11 10 CD m0 m1 m4 m5 m3 m2 m7 m6 m12 m13 m7 m8 m15 m14 m10 m9 5、逻辑函数的化简