南京大学：《电磁学》课程电子教案（教学课件）第二章 导体周围的静电场、静电能量

國电磁学02-03：库仑定律验证 ▣ Cavendish同心球实验结果和他自己的许多看法没有公开发表。 ▣I9世纪中叶，开尔文发现Cavendish的手稿中有圆盘和同半径的 圆球所带电荷的正确比值，才注意到这些手稿的价值，经他催促 ,才于1879年由Maxwell整理发表。 口他的许多重要发现埋藏了一百年之久。 口MaxwelⅡ说：“这些关于数学和电学实验的手稿近20捆，其中物体 上电荷（分布的实验，Cavendish-早就写好了详细的叙述，并且费 了很大气力书写得十分工整（就象要拿出去发表的样子），而且所 有这些工作在1774年以前就已完成，但Cavendish(并不急于发表) 仍是兢兢业业地继续做电学实验，直到1810年去世时，手稿仍在 他身边

电磁学02-03: 库仑定律验证  Cavendish同心球实验结果和他自己的许多看法没有公开发表。  19世纪中叶，开尔文发现Cavendish的手稿中有圆盘和同半径的 圆球所带电荷的正确比值，才注意到这些手稿的价值，经他催促 ，才于1879年由Maxwell整理发表。  他的许多重要发现埋藏了一百年之久。  Maxwell说： “这些关于数学和电学实验的手稿近20捆，其中物体 上电荷(分布)的实验，Cavendish早就写好了详细的叙述，并且费 了很大气力书写得十分工整(就象要拿出去发表的样子)，而且所 有这些工作在1774年以前就已完成，但Cavendish(并不急于发表) 仍是兢兢业业地继续做电学实验，直到1810年去世时，手稿仍在 他身边

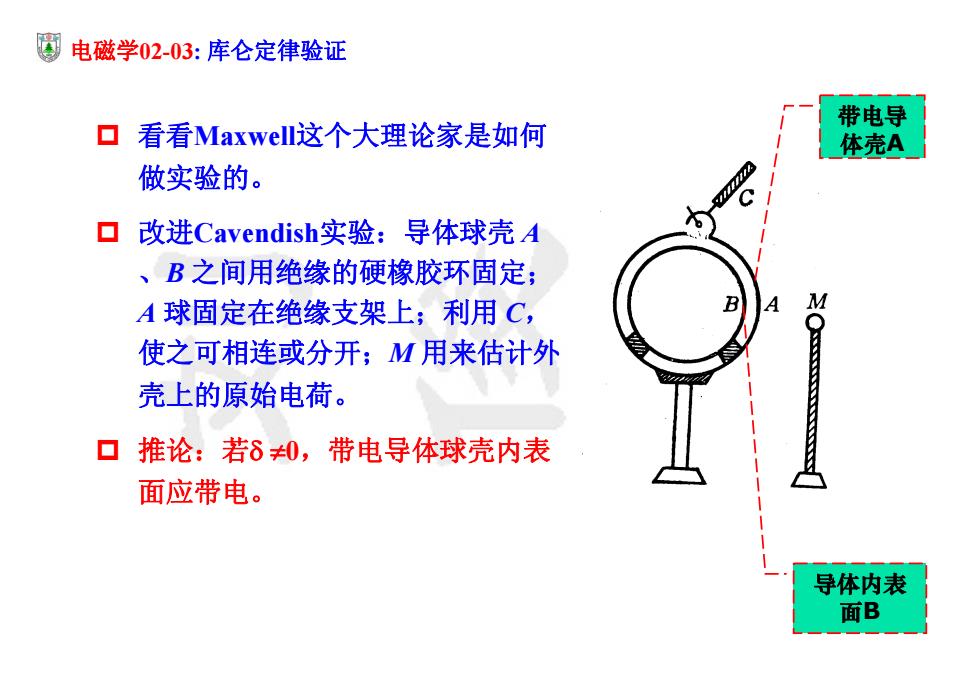
电磁学02-03：库仑定律验证 带电导 口看看Maxwelli这个大理论家是如何 体壳A 做实验的。 ▣改进Cavendish实验：导体球壳A 、B之间用绝缘的硬橡胶环固定； A球固定在绝缘支架上；利用C, M 使之可相连或分开；M用来估计外 壳上的原始电荷。 口推论：若δ，带电导体球壳内表 面应带电。 导体内表 面B

电磁学02-03: 库仑定律验证  看看Maxwell这个大理论家是如何 做实验的。  改进Cavendish实验：导体球壳 A 、B 之间用绝缘的硬橡胶环固定； A 球固定在绝缘支架上；利用 C， 使之可相连或分开；M 用来估计外 壳上的原始电荷。  推论：若 0，带电导体球壳内表 面应带电。 带电导 体壳A 导体内表 面B

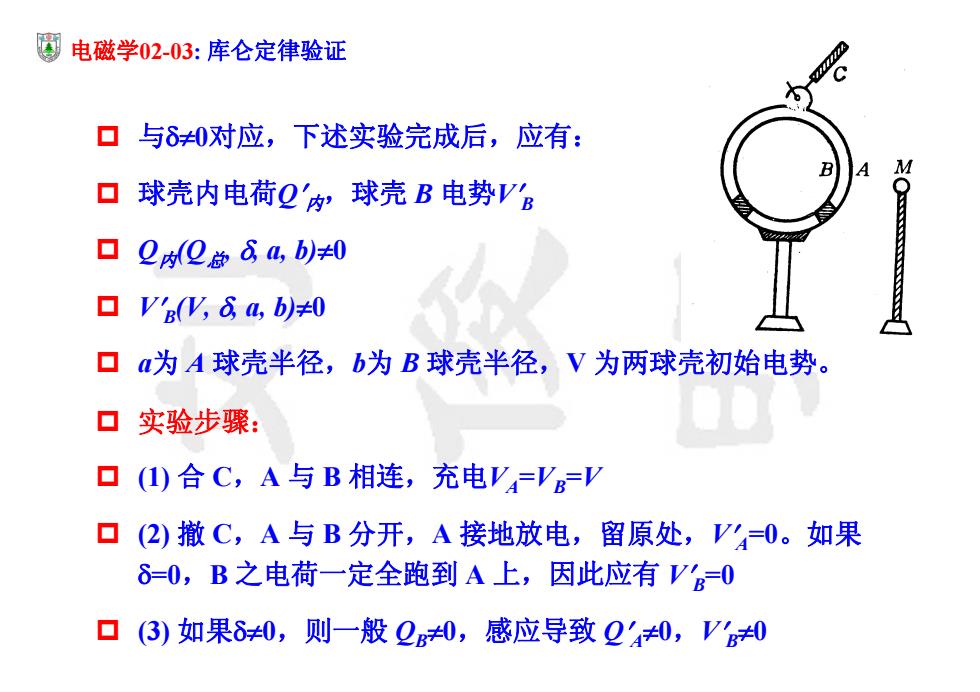
电磁学02-03：库仑定律验证 口与δ0对应，下述实验完成后，应有： 口球壳内电荷2'球壳B电势V6 口20点84，b)0 ▣Vs(%,8a,b)0 ▣a为A球壳半径，b为B球壳半径，V为两球壳初始电势。 口实验步骤： 口()合C,A与B相连，充电V=VV 口(2)撤C,A与B分开，A接地放电，留原处，V=0。如果 δ=0，B之电荷一定全跑到A上，因此应有VB=0 口(3)如果δ≠0，则一般20，感应导致2'0，V0

电磁学02-03: 库仑定律验证  与0对应，下述实验完成后，应有：  球壳内电荷Q内，球壳 B 电势VB  Q内(Q总, , a, b)0  VB(V, , a, b)0  a为 A 球壳半径，b为 B 球壳半径，V 为两球壳初始电势。  实验步骤：  (1) 合 C，A 与 B 相连，充电VA=VB=V  (2) 撤 C，A 与 B 分开，A 接地放电，留原处，VA=0。如果 =0，B 之电荷一定全跑到 A 上，因此应有 VB=0  (3) 如果0，则一般 QB0，感应导致 QA0，VB0

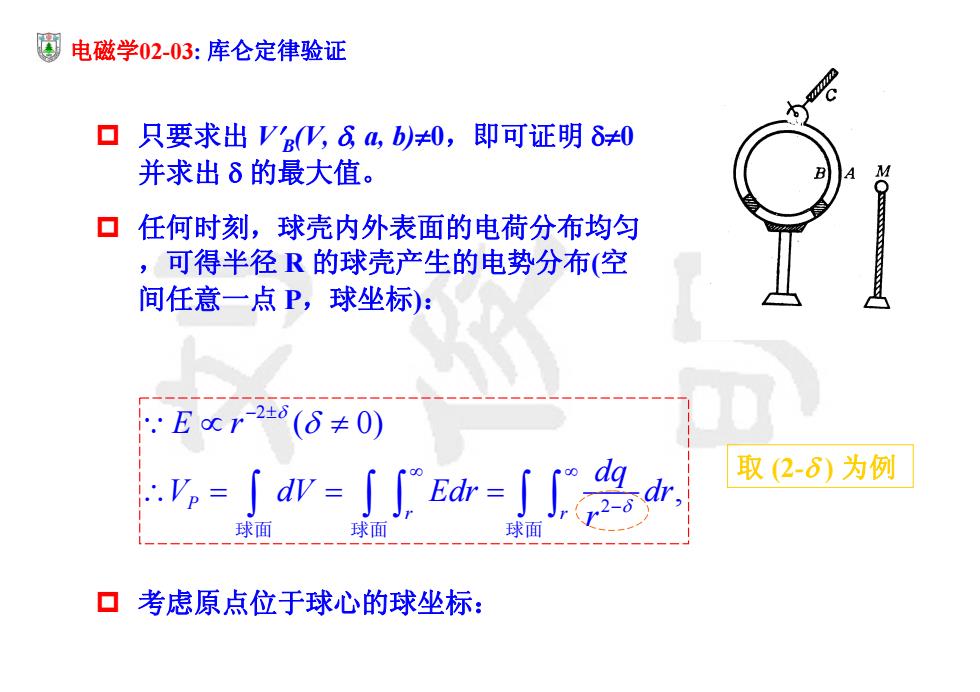
厦电磁学02-03：库仑定律验证 口只要求出Vs%,64,b)≠0，即可证明δ≠0 并求出δ的最大值。 ▣任何时刻，球壳内外表面的电荷分布均匀 ,可得半径R的球壳产生的电势分布（空 间任意一点P,球坐标)： E0r-2± (6≠0) 水=∫=∫a 取(2-6)为例 球面 球面 球面 ▣考虑原点位于球心的球坐标：

电磁学02-03: 库仑定律验证  只要求出 VB(V, , a, b)0，即可证明 0 并求出  的最大值。  任何时刻，球壳内外表面的电荷分布均匀 ，可得半径 R 的球壳产生的电势分布(空 间任意一点 P，球坐标)： 2 2 ( 0) , P r r E r dq V dV Edr dr r                  球面 球面 球面 取 (2- ) 为例  考虑原点位于球心的球坐标：

圆电磁学02-03：库仑定律验证 dg=oR'sinededo, (r)f(r)-rf(rdr R sinododedr sinodod r产I2.6n6eo .r2=R2+d2-2Rd cos0 面元 ah=RdsinOd0三∫I sinOdo Rd =ard0=2oLf）-fG160 d-R for d>R B=π→r=r=R+d,0=0→r=5={R-d for d<R 0 for d=R

电磁学02-03: 库仑定律验证 1 2 2 2 2 2 00 00 2 2 2 2 2 22 0 0 0 '( ) ( ) sin sin '( ) sin 1 sin , ( ) , '( ) ( ) 2 cos sin sin '( r r r P r P f r V r R d d dr R d dq R d d r f r r r dr r r R d Rd rdr rdr Rd d d R d r f r R dd r R d V f d                                                   1 2 1 2 2 1 2 0 , ) 2 [ () ()] 0 (1) 0 r r R r drd d R fr fr for d R r r R d r r R d for d R for d R d                          面元 R d  r O P