
閻 第二章导体周围的静电场,静电能量
第二章 导体周围的静电场,静电能量

圆电磁学02-01:导体 口导体的性质: 口第一类导体(金属,均匀) O,=constant 口电平衡弛豫时间极短(瞬时) system 口周围不存在电介质,绝缘材 E=∑E=J∬r)d" 料的相对介电常数为1, 0=∑u,=j∬uoaw 口电荷密度、静止等定义均指 宏观量。 重,Bs=∑0>dE=-vU= £0S呐 60 口静电平衡条件: ∮E·dl=0→oE=0 口均匀导体内部场强处处为零 dE=0 (inside conductor) 口每个均匀导体都是等势体; 口电荷静止不动(宏观)
电磁学02-01: 导体 导体的性质: 第一类导体(金属,均匀) 电平衡弛豫时间极短(瞬时) 周围不存在电介质,绝缘材 料的相对介电常数为1, 电荷密度、静止等定义均指 宏观量。 静电平衡条件: 均匀导体內部场强处处为零 每个均匀导体都是等势体; 电荷静止不动(宏观)。 2 0 0 constant ( ) ( ) 1 0 0 0 (inside conductor) i i i system i Q V i Q V S S S Q E E E r dV U U U r dV E dS Q divE U E dl rotE dE 内
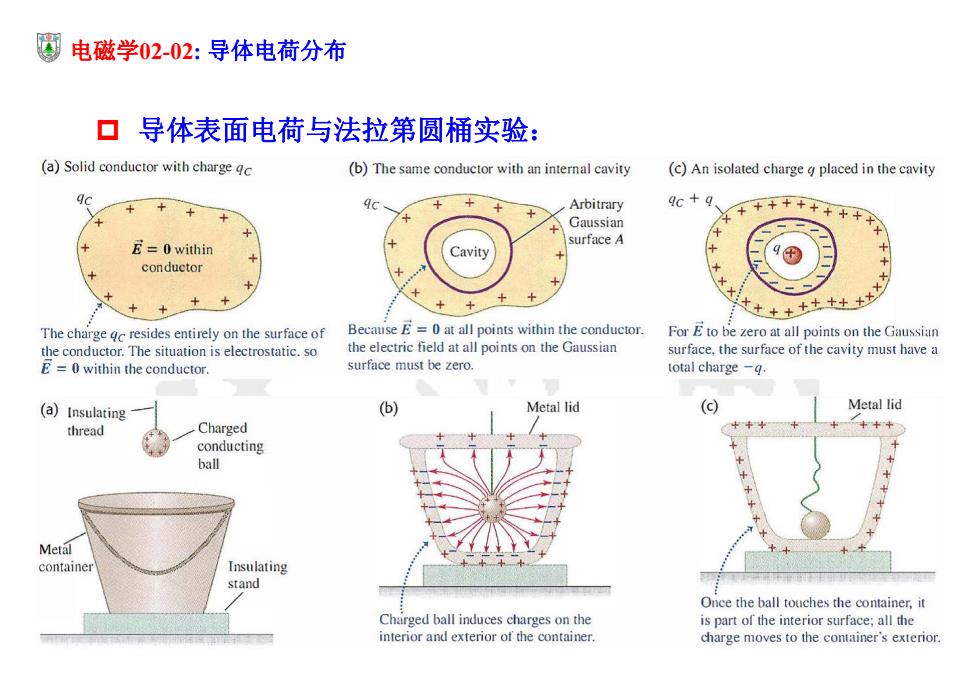
电磁学02-02:导体电荷分布 口导体表面电荷与法拉第圆桶实验: (a)Solid conductor with charge qc (b)The same conductor with an internal cavity (c)An isolated charge g placed in the cavity +十 + Arbitrary qc +q Gaussian =0 within surface A + Cavity + conductor + + The charge 4c resides entirely on the surface of Because E=0 at all points within the conductor. For Eto be zero at all points on the Gaussian the conductor.The situation is electrostatic.so the electric field at all points on the Gaussian surface,the surface of the cavity must have a E =0 within the conductor. surface must be zero. total charge -g. (a))Insulating (b) Metal lid () Metal lid thread Charged conducting ball Metal container Insulating stand Once the ball touches the container,it Charged ball induces charges on the is part of the interior surface;all the interior and exterior of the container. charge moves to the container's exterior
电磁学02-02: 导体电荷分布 导体表面电荷与法拉第圆桶实验:
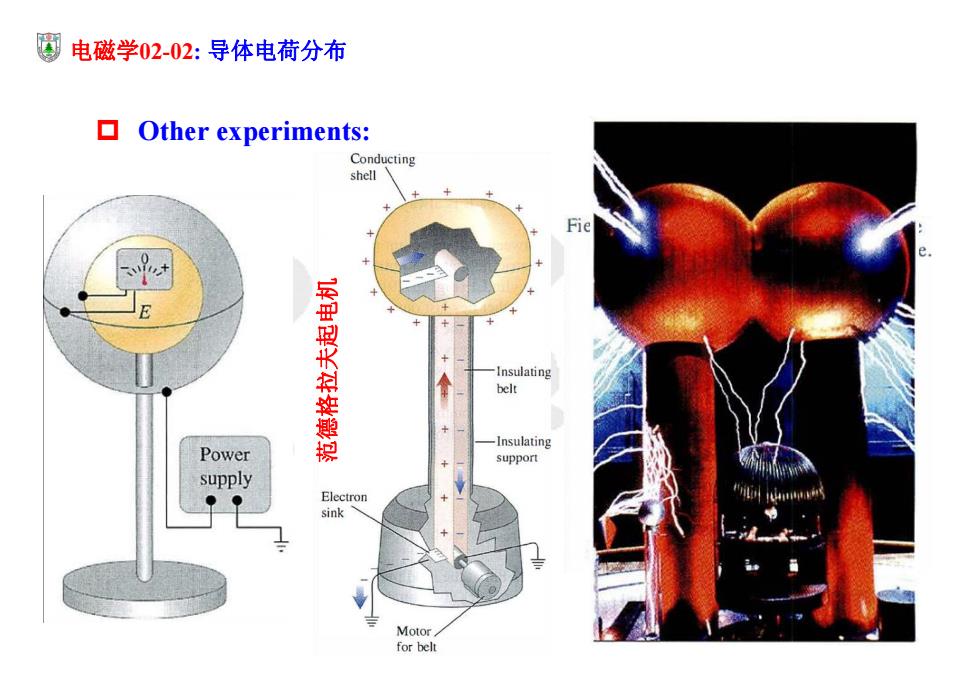
圆电磁学02-02:导体电荷分布 ▣Other experiments: Conducting shell Fie -Insulating belt -Insulating Power support supply Electron sink Motor for belt
电磁学02-02: 导体电荷分布 Other experiments: 范德格拉夫起电机
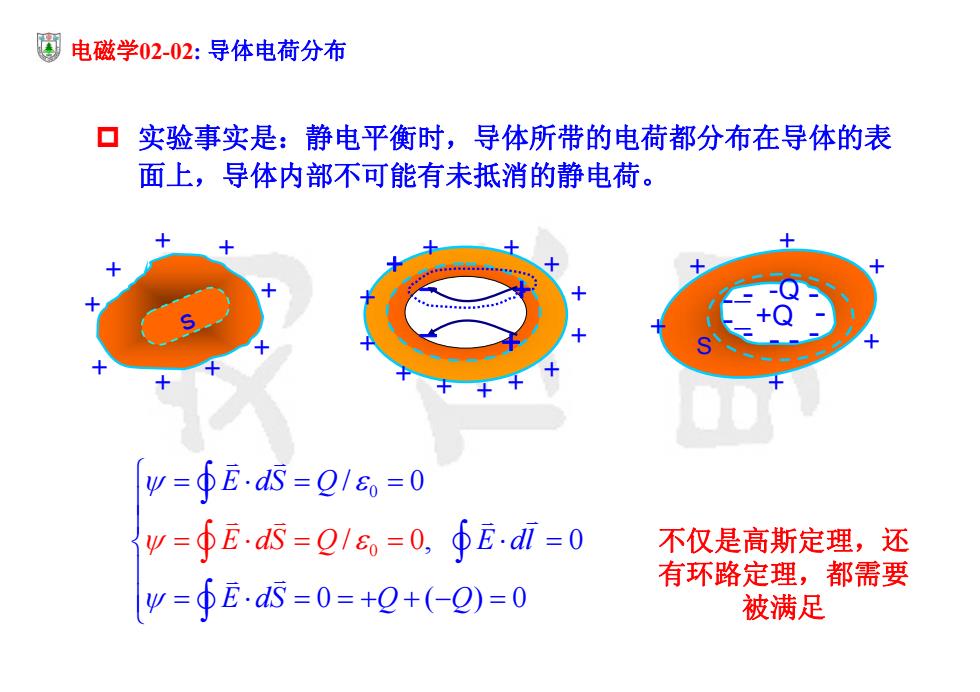
电磁学02-02:导体电荷分布 ▣实验事实是:静电平衡时,导体所带的电荷都分布在导体的表 面上,导体内部不可能有未抵消的静电荷。 w=∮E.d=0/6=0 w=∮Eds=0/6=0,fEdl=0 不仅是高斯定理,还 有环路定理,都需要 w=∮E.S=0=+9+(-2)=0 被满足
电磁学02-02: 导体电荷分布 实验事实是:静电平衡时,导体所带的电荷都分布在导体的表 面上,导体内部不可能有未抵消的静电荷。 + + + + + + + + + s + _ _ + + + + + +Q -Q S - - - - - - - - - 0 0 / 0 / 0, 0 0 ( )0 E dS Q E dl E dS E S Q d Q Q + + + + + + + + + + + + + - + - + 不仅是高斯定理,还 有环路定理,都需要 被满足