
厦电磁学02-02:导体电荷分布 口【例2.1.7】一导体球壳A带有电荷量q4<0,导体小球B带有电 荷量q0。用绝缘丝带吊起小球B经小孔放入球壳A内。 ()B与A不接触,另A瞬时接地,然后断开接地,将B取出。球壳 A与小球B带电情况如何? (2)B与A的内壁接触,A不接地,然后将B取出。球壳A与小球B 带电情况如何? 静电平衡条件下上面的球 壳内表面有电荷么?
电磁学02-02: 导体电荷分布 【例2.1.7】一导体球壳 A 带有电荷量 qA<0,导体小球 B 带有电 荷量 qB>0。用绝缘丝带吊起小球B经小孔放入球壳A内。 (1) B与A不接触,另A瞬时接地,然后断开接地,将B取出。球壳 A与小球B带电情况如何? (2) B与A的内壁接触,A不接地,然后将B取出。球壳A与小球B 带电情况如何? 静电平衡条件下上面的球 壳内表面有电荷么?
电磁学02-03:库仑定律验证(来自北大李芳华教案) 口源于Cavendish-Maxwell多年的工作, ▣Cavendish(1731-1810)设想:库仑力Facr-2t6cr-",,若δ≠0,则 均匀带电导体球壳内表面将带电。找出此函数关系(理论),比较 Q内与Q总(实验),便可确定δ的下限。 o d ds ds
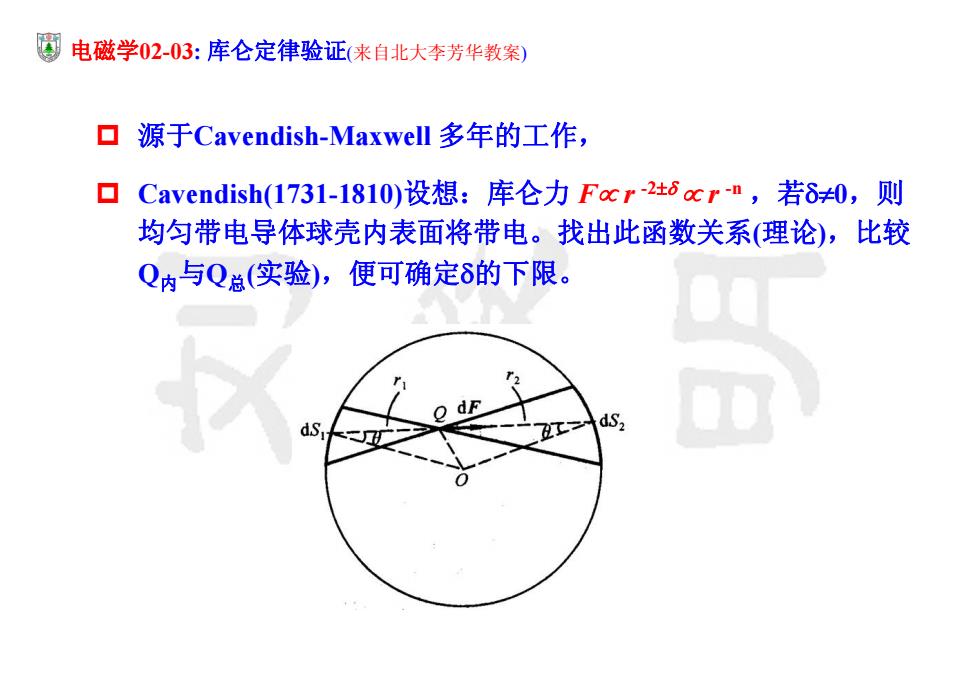
电磁学02-03: 库仑定律验证(来自北大李芳华教案) 源于Cavendish-Maxwell 多年的工作, Cavendish(1731-1810)设想:库仑力 F r -2 r -n ,若0,则 均匀带电导体球壳内表面将带电。找出此函数关系(理论),比较 Q内与Q总(实验),便可确定的下限
厦电磁学02-03:库仑定律验证 口首先,若δ0,则均匀带电球面对内部任意点电 荷作用力不为零。球面电荷密度σ。位于球内任 意电荷Q受电荷元olS,和olS,的共同作用。 odS2σdS, ,·dQ=Scos0 ds,cos r ∴.dFoc oOdg cos0 n-2 g)→n=2→df=0 口电荷在球壳内任一点处(除球心外)都受到电场力; 口结论:若δ0,均匀带电球壳在球内各处场强不严格为 零(球心除外)
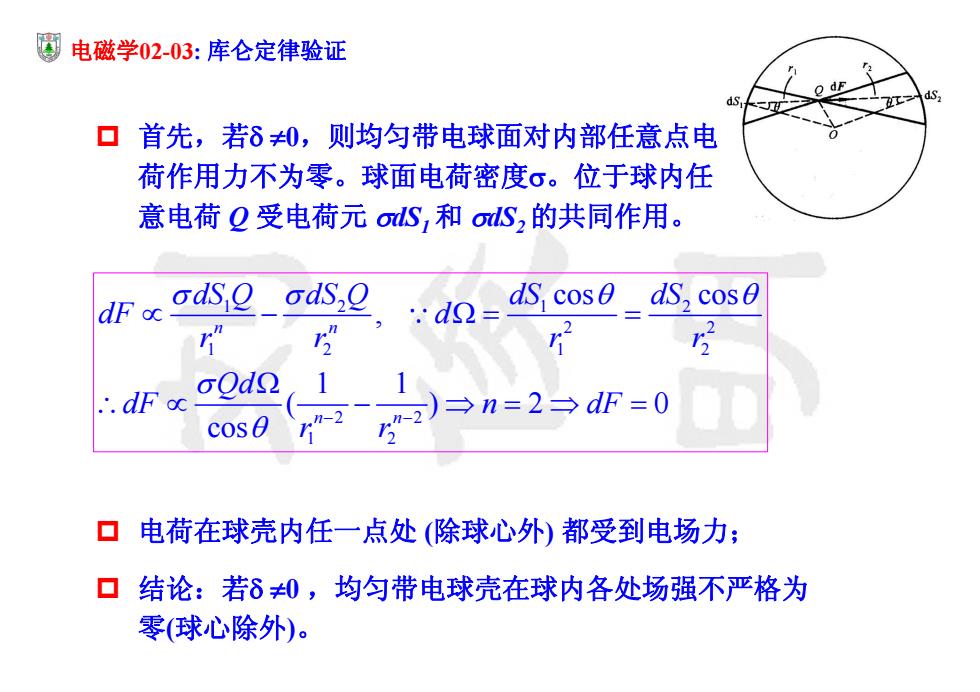
电磁学02-03: 库仑定律验证 首先,若 0,则均匀带电球面对内部任意点电 荷作用力不为零。球面电荷密度。位于球内任 意电荷 Q 受电荷元 dS1 和 dS2 的共同作用。 12 1 2 2 2 12 1 2 2 2 1 2 cos cos , 1 1 ( )2 0 cos n n n n dS Q dS Q dS dS dF d rr r r Qd dF n dF r r 电荷在球壳内任一点处 (除球心外) 都受到电场力; 结论:若 0 ,均匀带电球壳在球内各处场强不严格为 零(球心除外)
电磁学02-03:库仑定律验证 口推论:若δ0,带电导体球壳内表面应带电。 ▣δ0时,若内表面无电荷分布(只分布在外表面),使导体中自由 电子因受力或趋向球心运动,或背离球心而移动,最终使电荷 分布满足导体内场强处处为零的条件一内表面有电荷分布。 带电导 体壳 ds. 所谓导体,就是其内部 导体内表面 球壳内部)有取之不尽 用之不竭的电荷(电子)
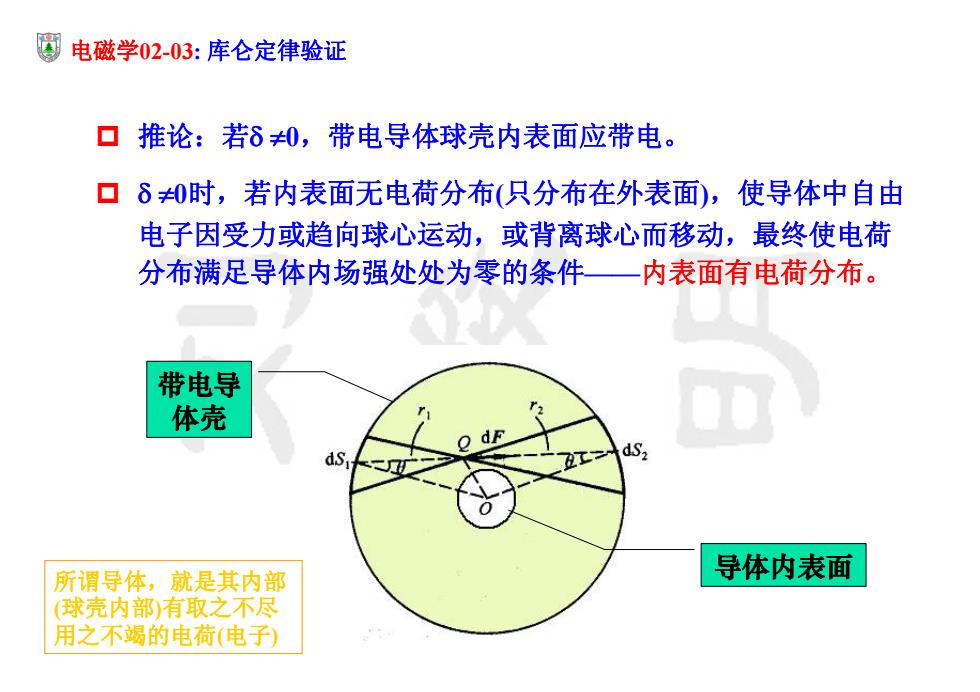
电磁学02-03: 库仑定律验证 推论:若 0,带电导体球壳内表面应带电。 0时,若内表面无电荷分布(只分布在外表面),使导体中自由 电子因受力或趋向球心运动,或背离球心而移动,最终使电荷 分布满足导体内场强处处为零的条件——内表面有电荷分布。 导体内表面 带电导 体壳 所谓导体,就是其内部 (球壳内部)有取之不尽 用之不竭的电荷(电子)

圆电磁学02-03:库仑定律验证 口1773年:“我取一个直径为12.1英寸的球 ,用一根实心的玻璃棒穿过中心当作轴 并覆盖以封蜡。...然后把这个球封 在两个中空的半球中间,半球直径为 13.3英寸,120英寸厚。...然后,我 用一根导线将莱顿瓶的正极接到半球, 使半球带电。” 绝缘支柱 ▣用一根导线将内外球联在一起,外球壳 木髓球 验电器 带电后,取走导线,打开外球壳,用木 髓球验电器试验内球。 口木髓球验电器没有指示,证明内球没带 电,指数6≤0.02
电磁学02-03: 库仑定律验证 1773年:“我取一个直径为12.1英寸的球 ,用一根实心的玻璃棒穿过中心当作轴 ,并覆盖以封蜡。……然后把这个球封 在两个中空的半球中间,半球直径为 13.3英寸,1/20英寸厚。……然后,我 用一根导线将莱顿瓶的正极接到半球, 使半球带电。” 用一根导线将内外球联在一起,外球壳 带电后,取走导线,打开外球壳,用木 髓球验电器试验内球。 木髓球验电器没有指示,证明内球没带 电,指数0.02