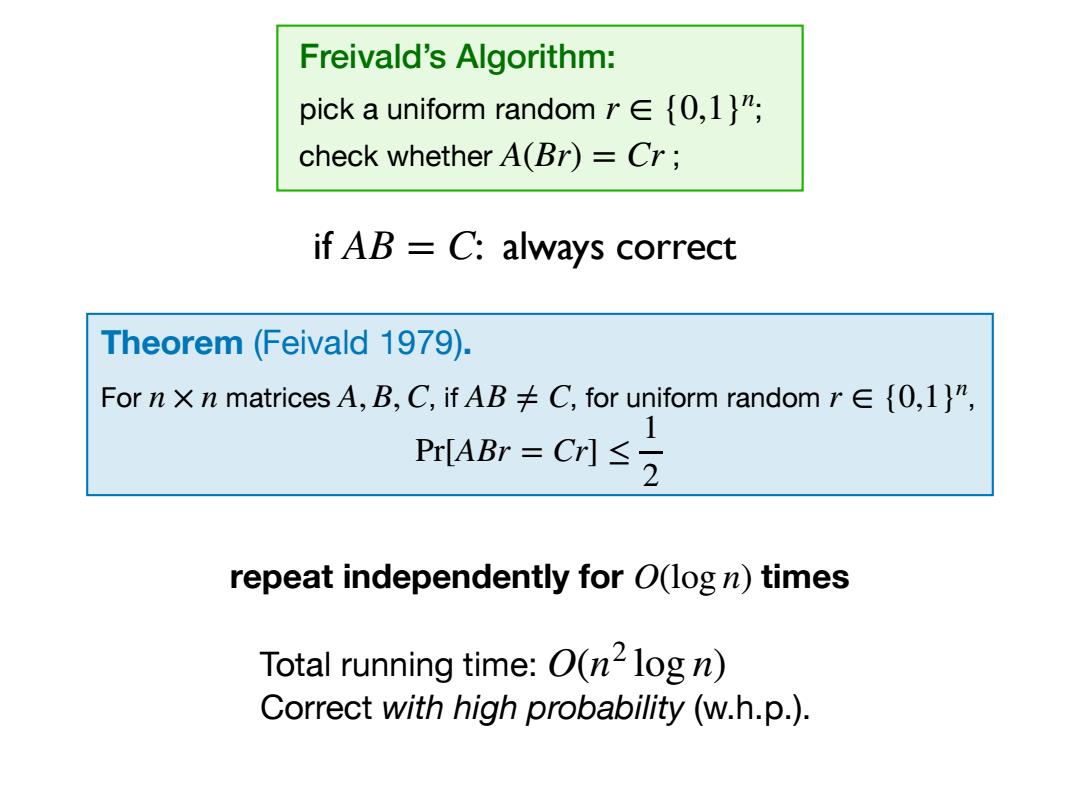
Freivald's Algorithm: pick a uniform random r {0,1)"; check whether A(Br)=Cr; if AB C:always correct Theorem(Feivald 1979). For n X n matrices A,B,C,ifAB≠C,for uniform random r∈{0,l}n, Pr[ABr=Cr]≤ 2 repeat independently for O(log n)times Total running time:O(n2log n) Correct with high probability (w.h.p.)
Freivald’s Algorithm: pick a uniform random ; check whether ; r ∈ {0,1}n A(Br) = Cr Theorem (Feivald 1979). For n × n matrices A, B,C, if AB ≠ C, for uniform random r ∈ {0,1} , n Pr[ABr = Cr] ≤ 1 2 if AB = C: always correct repeat independently for O(log n) times Total running time: Correct with high probability (w.h.p.). O(n2 log n)

Polynomial Identity Testing (PIT) Input:two polynomials fg E Fx]of degree d. Output:f三g? Fx]:polynomial ring in x over field F f∈rL]of degree d:f)=∑a where a,∈F =0 field Input:a polynomial fE Fx]of degree d. Output:f三0? fis given as black-box
Polynomial Identity Testing (PIT) Input: two polynomials of degree . Output: ? f, g ∈ 𝔽[x] d f ≡ g Input: a polynomial of degree . Output: ? f ∈ 𝔽[x] d f ≡ 0 f ∈ 𝔽[x] of degree d: f(x) = where d ∑ i=0 ai xi ai ∈ 𝔽 f is given as black-box field 𝔽[x]: polynomial ring in x over field 𝔽

Input:a polynomial fE Fx]of degree d. Output:f三0? Deterministic algorithm (polynomial interpolation): pick arbitrary distinct., check if f(x)=0 for all0≤i≤d; Fundamental Theorem of Algebra. Any non-zero d-degree polynomial fE Fx]has at most d roots. Randomized algorithm(fingerprinting): pick a uniform random re S; let S Fbe arbitrary check if f(r)=0; (whose size to be fixed later)
Input: a polynomial of degree . Output: ? f ∈ 𝔽[x] d f ≡ 0 • Deterministic algorithm (polynomial interpolation): pick arbitrary distinct ; check if for all ; x0, x1, …, xd ∈ 𝔽 f(xi ) = 0 0 ≤ i ≤ d • Randomized algorithm (fingerprinting): pick a uniform random ; check if ; r f(r) = 0 ∈ S let be arbitrary (whose size to be fixed later) S ⊆ 𝔽 Fundamental Theorem of Algebra. Any non-zero d-degree polynomial f ∈ 𝔽[x] has at most d roots

Input:a polynomial fE Fx]of degree d. Output:f三0? pick a uniform random re S; let S Fbe arbitrary check if f(r)=0; (whose size to-be fixed later) |S|=2d iff≡O:always correct ff丰0: Pr[fr)=O]≤ d 1 ISI 2 Fundamental Theorem of Algebra. Any non-zero d-degree polynomial f Fx]has at most d roots
pick a uniform random ; check if ; r f(r) = 0 ∈ S let be arbitrary (whose size to be fixed later) S ⊆ 𝔽 if f ≡ 0: always correct Input: a polynomial of degree . Output: ? f ∈ 𝔽[x] d f ≡ 0 if f ≢ 0: Pr[f(r) = 0] ≤ |S| Fundamental Theorem of Algebra. Any non-zero d-degree polynomial f ∈ 𝔽[x] has at most d roots. d |S| = 2d = 1 2
Checking Identity 北京 database 1 Are they identical? 南京 database 2
Checking Identity database 1 database 2 Are they identical? 北京 南京