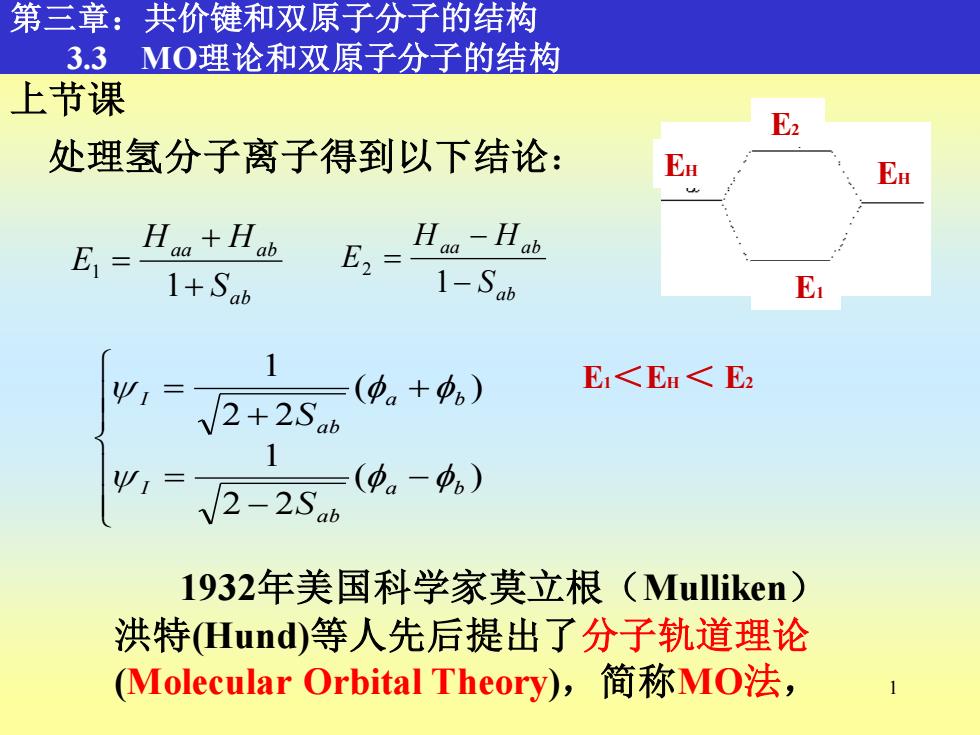
第三章:共价键和双原子分子的结构 3.3MO理论和双原子分子的结构 上节课 E2 处理氢分子离子得到以下结论: Ea Ea E=月+H 1+Sab E2= Haa-Hab 1-Sab E Ψ1= (中。+中) E<E<E2 √2+2Sab 2-2Sab (φ。-中。) 1932年美国科学家莫立根(Mulliken) 洪特Hund)等人先后提出了分子轨道理论 (Molecular Orbital Theory),简称MO法
1 1932年美国科学家莫立根(Mulliken) 洪特(Hund)等人先后提出了分子轨道理论 (Molecular Orbital Theory),简称MO法, 第三章:共价键和双原子分子的结构 3.3 MO理论和双原子分子的结构 E1 E2 EH EH E1<EH < E2 上节课 处理氢分子离子得到以下结论: − − = + + = ( ) 2 2 1 ( ) 2 2 1 a b a b I a b a b I S S ab aa ab S H H E + + = 1 1 ab aa ab S H H E − − = 1 2

第三章:共价键和双原子分子的结构 3.3MO理论和双原子分子的结构分子轨道理论的基本要点 1、分子轨道理论的基本观点是把分子看作 一个整体,其中电子不再从属于某一个原子 而是在整个分子的势场范围内运动。 正如在原子中每个电子的运动状态可用波 函数(业)来描述那样,分子中每个电子的 运动状态也可用相应的波函数来描述
2 1、分子轨道理论的基本观点是把分子看作 一个整体,其中电子不再从属于某一个原子 而是在整个分子的势场范围内运动。 正如在原子中每个电子的运动状态可用波 函数(ψ)来描述那样,分子中每个电子的 运动状态也可用相应的波函数来描述。 第三章:共价键和双原子分子的结构 3.3 MO理论和双原子分子的结构 分子轨道理论的基本要点

第三章:共价键和双原子分子的结构 3.3MO理论和双原子分子的结构分子轨道理论的基本要点 2、分子轨道是由分子中原子的原子轨道线性组合而成, 简称LCAO(linear combination of atomic orbitals的缩写) 组合形成的分子轨道数目与组合前的原子轨道数目相等。 如两个原子轨道Ψ,和w线性组合后形成两个分子轨道Ψ和Ψ2 Ψ1=C1Ψa+C2Ψb Ψ2=C1ΨaC2Ψb 这种组合和杂化轨道不同,杂化轨道是同一原子内部能 量相近的不同类型的轨道重新组合,而分子轨道却是由不同 原子提供的原子轨道的线性组合。 原子轨道用s、p、d、f.表示, 分子轨道则用σ、π、δ.表示。 3
3 2、分子轨道是由分子中原子的原子轨道线性组合而成, 简称LCAO (linear combination of atomic orbitals的缩写)。 组合形成的分子轨道数目与组合前的原子轨道数目相等。 如两个原子轨道ψa和ψb线性组合后形成两个分子轨道ψ1和ψ2 ψ1 =c1ψa +c2ψb ψ2=c1ψa - c2ψb 第三章:共价键和双原子分子的结构 3.3 MO理论和双原子分子的结构 分子轨道理论的基本要点 这种组合和杂化轨道不同,杂化轨道是同一原子内部能 量相近的不同类型的轨道重新组合,而分子轨道却是由不同 原子提供的原子轨道的线性组合。 原子轨道用s、p、d、f.表示, 分子轨道则用σ、π、δ.表示

第三章:共价键和双原子分子的结构 3.3MO理论和双原子分子的结构 分子轨道理论的基本要点 3、原子轨道线性组合成分子轨道后,分子轨 道中能量高于原来的原子轨道者称为反键轨道, 能量低于原来的原子轨道者称为成键轨道。 E2 o-B Ea Ea E
4 3、原子轨道线性组合成分子轨道后,分子轨 道中能量高于原来的原子轨道者称为反键轨道, 能量低于原来的原子轨道者称为成键轨道。 第三章:共价键和双原子分子的结构 3.3 MO理论和双原子分子的结构 分子轨道理论的基本要点 E1 E2 EH EH
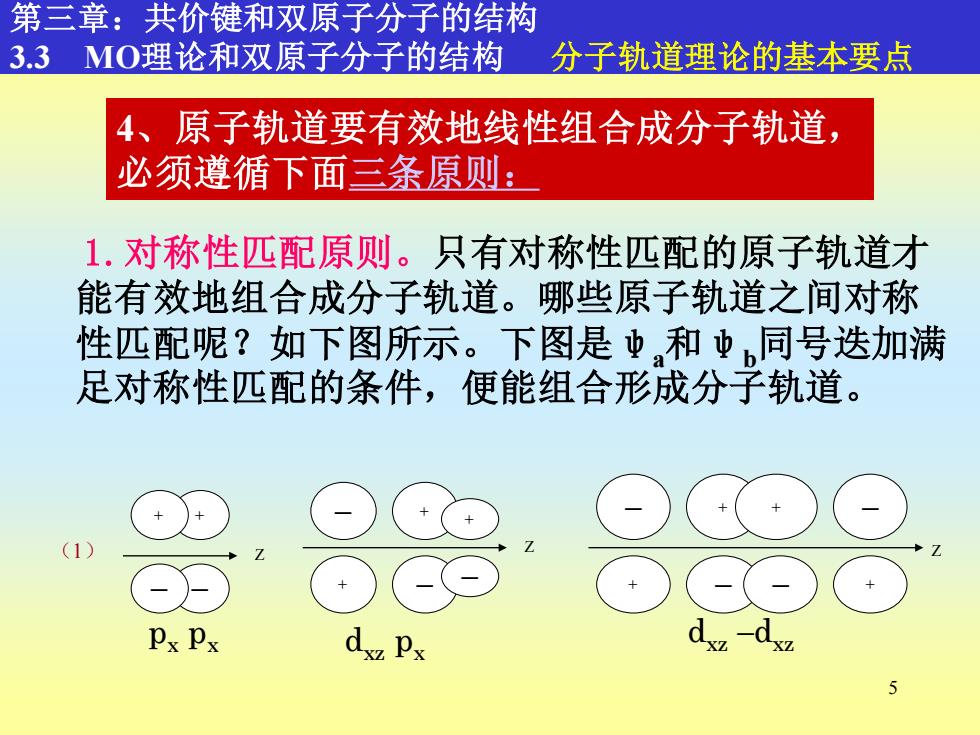
第三章:共价键和双原子分子的结构 3.3MO理论和双原子分子的结构 分子轨道理论的基本要点 4、原子轨道要有效地线性组合成分子轨道, 必须遵循下面三条原则: 1.对称性匹配原则。只有对称性匹配的原子轨道才 能有效地组合成分子轨道。哪些原子轨道之间对称 性匹配呢?如下图所示。下图是中和虫同号迭加满 足对称性匹配的条件,便能组合形成分子轨道。 Px Px XZ 5
5 1.对称性匹配原则。只有对称性匹配的原子轨道才 能有效地组合成分子轨道。哪些原子轨道之间对称 性匹配呢?如下图所示。下图是ψa和ψb同号迭加满 足对称性匹配的条件,便能组合形成分子轨道。 4、原子轨道要有效地线性组合成分子轨道, 必须遵循下面三条原则: 第三章:共价键和双原子分子的结构 3.3 MO理论和双原子分子的结构 分子轨道理论的基本要点 + — Z + — (1) px px — + + — + — Z dxz px — + + — + — — + Z dxz –dxz