
例10.1.1用最速下降法求非线性规划问题 min f(X)=x2+25x, 取初始点X0=(2,2),允许误差ε=10-6。 解:f(X0)=104,Vf(x)=(2x1,50x2), Vf(X0)=(4,100) )fX0=V42+1002=10016 由 2Xo0+d)=0得元,=0.02003。 故 X0=Xo-27f(Xo)=(1.92,-0.003) f(X0)=3.69
例10.1.1 用最速下降法求非线性规划问题 (0) ( ) (4,100)T = f X 1 2 ( ) (2 ,50 ) , T = f x x x (0) f X( ) 104, = 6 10− X (0) = (2,2) , T = 。 2 2 min ( ) 25 1 2 f X x x = + 取初始点 允许误差 解: 0 2 2 = + = f X 4 100 10016 ( ( ) ) (1) f X( ) 3.69 = (1) (0) (0) 0 ( ) (1.92, 0.003)T X X f X = − = − d f X d ( ) 0 (0) (0) 故 d 由 + = 得 0 = 0.02003

前三次迭代过程如表1。 表1 迭代 次数 点 X X2 f(X() f(x) 0 YO) 0.02003 2 2 (4,100)7 104 1 X四 0.4824 1.92 -0.003 (3.84,-0.15) 3.69 X(2) 2 0.020 0.07 0.070 (0.14,3.50) 0.13 P(3) 3 0.07 -0.000 经过10轮迭代,即可满足允许误差£=10-6的 要求,迭代过程的几何表示如图10.1.1
前三次迭代过程如表1。 表1 迭代 次数 点 0 0.02003 2 2 104 1 0.4824 1.92 -0.003 3.69 2 0.020 0.07 0.070 0.13 3 —— 0.07 -0.000 —— —— 6 10− = (0.14,3.50)T (3.84, 0.15)T − 4,100) ( T (3) X (2) X (1) X 0 X ( ) ( ) ( ) k f X ( ) ( ) k k x1 x2 f X 经过10轮迭代,即可满足允许误差 的 要求, 迭代过程的几何表示如图10.1.1
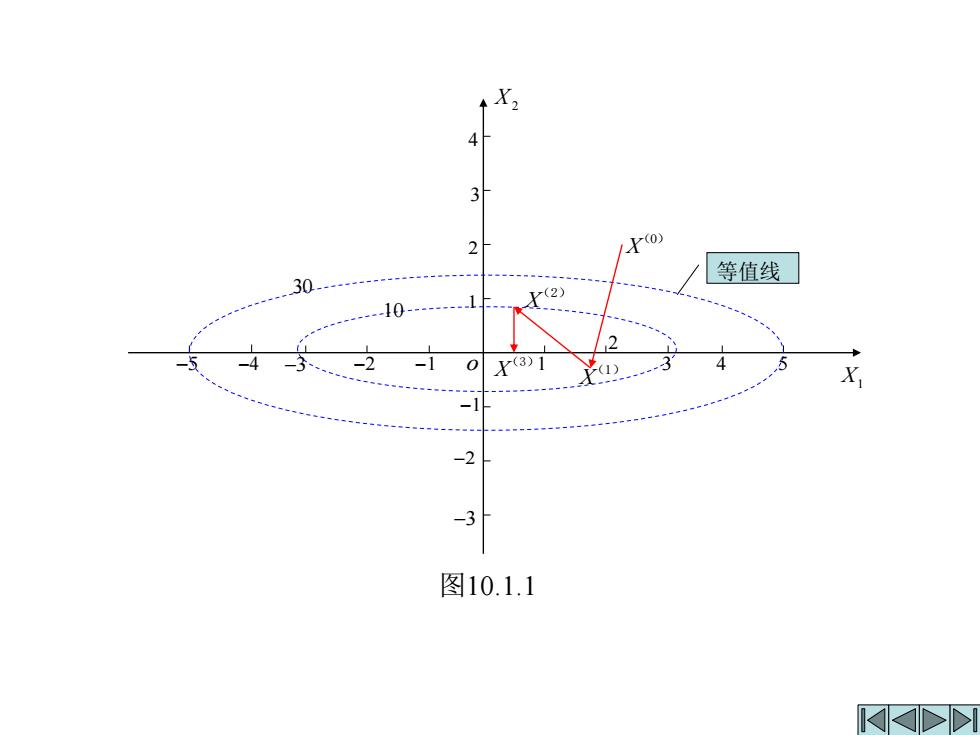
4 3 2 等值线 30 - -(2) 10 2 -4 -3 -1 0 X3)1 4 5 X -2 -3 图10.1.1
0 X ( ) X1 1 X (3) X (2) X −5 −4 1 (1) −3 −2 −1 4 3 2 −3 −2 −1 3 4 5 2 X2 o 10 30 等值线 图10.1.1

由图10.1.1可知,Xk随着迭代次数的增加,越 来越接近于最优解(0,0)严,但是我们也应该注意到 一个问题,随着迭代次数的增加,收敛速度越来越 慢,在极小点附近,X逼近最优解的路径呈锯齿 形,这种现象称为“锯齿现象这种算法的依据仍 然是梯度。梯度是用来刻画函数的局部性质的,在 某一点的邻域内函数值下降最快,但从求解极小点 的全部过程来看并不一定最快。 虽然最速下降法收敛速度较慢,但它却因方法 简便,计算量和存贮量少而被人们广泛使用,在实 际运用时,常将最速下降法和其它方法结合使用。 在前期使用最速下降法,而在接近极小点时则改用 其它收敛较快的方法
由图10.1.1可知, 随着迭代次数的增加, (0,0 , )T ( ) k X 越 来越接近于最优解 但是我们也应该注意到 一个问题,随着迭代次数的增加,收敛速度越来越 慢,在极小点附近, ( ) k X 逼近最优解的路径呈锯齿 形,这种现象称为“锯齿现象”。这种算法的依据仍 然是梯度。梯度是用来刻画函数的局部性质的,在 某一点的邻域内函数值下降最快, 的全部过程来看并不一定最快。 但从求解极小点 虽然最速下降法收敛速度较慢,但它却因方法 简便,计算量和存贮量少而被人们广泛使用,在实 际运用时,常将最速下降法和其它方法结合使用。 在前期使用最速下降法,而在接近极小点时则改用 其它收敛较快的方法

§10.2 牛顿法 10.2.1 牛顿法 设f(x)是二次可微实函数,x∈R”.又设xk)是f(x)的极小点 的一个估计,我们把f(x在xk)展成Taylor级数,并取二阶近似: f(x)≈(x) f(x()+Vf(x()"(x-x)) +(-xyVf(x"Xx-x) 其中V2f(x)是f(x)在xk)处的Hesse矩阵.为求x)的平稳 点,令 V(x)=0 即 Vf(x()+v2f(x)(x-x)=0 (10.2.1)
§10.2 牛顿法 10.2.1 牛顿法 设 是二次可微实函数, .又设 是 的极小点 的一个估计,我们把 在 展成Taylor级数,并取二阶近似: f (x) n x R (k ) x f (x) f (x) (k ) x ( ) ( )( ) 2 1 ( ) ( ) ( ) ( ) ( ) ( ) 2 ( ) ( ) ( ) ( ) ( ) k T k k k k T k x x f x x x f x f x x x f x x + − − = + − 其中 是 在 处的Hesse矩阵. 为求 的平稳 点,令 ( ) 2 (k ) f x f (x) (k ) x (x) (x) = 0 ( ) ( )( ) 0 ( ) 2 ( ) ( ) + − = k k k 即 f x f x x x (10.2.1)