
1家庭作业·数学·七年级·下册·配北师大版 解马老以吃亏了.理由如下: 【方法归纳】 .'a2-(a+5)(a-5)=a2-(a2-25)= a2-a2+25=25, 解决这类问题首先要表示出图形中所求 与原来相比,马老以的土地面积减少 部分的面积,再利用作差法比较大小 了25m,马老以吃亏了. 新知·训练巩固 1.已知a=2020,b=2021×2019,则(B). 解原式=(7-1)(7+1)(72+1)(7+1) A.a=b B.a>b (78+1)(716+1)+1=(72-1)(72+1) C.a<b D.a≤b (74+1)(78+1)·(716+1)+1=(7-1) 2.简便计算:2018×2020-20192=-1. (7+1)(78+1)(76+1)+1=(78-1) 3.化简:6×(7+1)×(72+1)×(74+1)× (78+1)(716+1)+1=(716-1)(716十1)+ (78+1)×(76+1)+1.(结果用幂的形式 1=732-1十1=732. 表示) 素能·演练提升 1.有三种长度分别为三个连续整数的木棒若 干根,小明利用中等长度的木棒摆成了一 2(a-b(a+b)=号(a2-B)=2×40- 个正方形,小刚用其余两种长度的木棒摆 20. 出了一个长方形,正方形和长方形每边只 4.如图,从边长为(十3)的正方形纸片剪下 有一根木棒,那么摆得面积最大的是 一个边长为m的正方形后,剩余部分可剪 (B). 拼成一个长方形(不重叠无缝隙).若拼成 A.小刚 B.小明 的长方形的一边长为3,则这个长方形的周 C.同样大 D.无法比较 长是多少? 2.定义a※b=a(b+1),例如2※3=2×(3十1) 2×4=8.则(x一1)※x的结果为x2一1 -m+3 3.如图,若大正方形与小 正方形的面积之差是 解由面积的和、差,得长方形的面积为 40,则阴影部分的面积 (m+3)2-m2=(m+3十m)(m+3-m)= 是多少? 3(2m+3). B 由长方形的宽为3,可得长方形的长为 解设大正方形边长为a,小正方形边长为 (2m+3). b,,大正方形与小正方形的面积之差为 故长方形的周长为2[(2m+3)十 40,∴.a-b=40,∴.AE=AB-BE=a-b, 3]=4m+12. SH载=SAXE十SAE=2AE·BC斗 2AE·BD=(a-b)a十2(a-b)b= 24

第一章整式的乘除、 6.完全平方公式 第1课时完全平方公式 基础·自主梳理 1.两数和的完全平方公式:(a十b)2= 的二项式相乘(即二项式的平方); a2+2ab+b2. (2)右边是三项,首尾两项分别是二项 2.两数差的完全平方公式:(a一b)2= 式两项的平方,中间一项是二项式两项 a2-2ab+b2. 积的2倍. 3.两数和(或差)的平方,等于它们的平 2.公式右边2ab的符号取决于左边二 方和加上(或减去)它们积的2倍: 项式中两项的符号.若这两项同号,则2ab 温馨提示 取“十”;若这两项异号,则2ab的符号 1.公式的特征:(1)左边是两个相同 为“一” 核心·重难探究 知识点一完全平方公式 (x2-9)=x2+4x+4+2x2-4x-16-r2+ 【例1】计算:(1)(-2m+n)2; 9=2x2-3. (2)(-2m-n)2; (5)(a+3)2-(a-3)2-3a(2a-1)+ (3)(2a+b)2-(2a-b)2; (a+1)(a-1)=(a2+6a+9)-(a2-6a+ (4)(x+2)2+2(x十2)(x-4)-(x+3)· 9)-6a2+3a+(a2-1)=a2+6a+9-a2+ (x-3): 6a-9-6a2+3a+a2-1=-5a2+15a-1. (5)(a+3)2-(a-3)2-3a(2a-1)+ 【方法归纳】 (a+1)(a-1). 思路点拨弄清题目中所包含的运算及 运用完全平方公式时,首先要确定用 运算顺序是解题的关键, “和”还是用“差”,然后根据选择的“和”与 解(1)(-2m+n)2=(2m)2-2·2m· “差”确定谁相当于公式中的“a”,谁相当于公 n+n2=4m2-4mn十n2. 式中的“b”,最后直接利用公式计算 (2)(-2m-n)2=(-2m)2+2· 知识点二整式的化简、求值 (-2m)·(-n)+(-n)2=4m2+4n十n2. 【例2】先化简,再求值:4(x十1)2一 (3)(2a+b)2-(2a-b)2=(4a2+4ab+ b)-(4a2-4ab+b2)=8ab. 7-1)(+1D+31-x)3,其中=- (4)(x+2)2+2(x+2)(x-4)-(x+ 思路点拨首先对所给的式子进行化简, 3)(x-3)=(x2+4x+4)+2(x2-2x-8)- 然后代入数值计算即可. 25

儿家庭作业·数学·七年级·下册·配北师大版 解4(x+1)2-7(x-1)(x+1)+3(1一 14=13. x)2=4(x2+2x+1)-7(x2-1)+3(1-2x+ 【方法归纳】 x2)=4x2+8x+4-7x2+7+3-6x+3x2= 对于整式的化简、求值问题要注意运算 2x+14, 顺序不能出错,代入求值时要注意负数的有 省x=一 时,原式=2×(-》 关计算要加括号,分数的乘方要加括号. 新知·训练巩固 1.下列多项式乘法中,能用完全平方公式计 4.计算:(x-y)2十x(.x十2y). 算的是(C). 解(x-y)+x(x+2y)=x2-2xy+y2+ A.(a+1)(-a+1) x2+2xy=2x2+y2. B.(a+b)(b-a) 5.先化简,再求值: C.(-a+b)(a-b) x2(.x-1)-(x-1)2-(x+3)(x-3),其中 D.(a-b)(a+b) x 2.下列运算正确的是(B). A.(a+b)2=a2+b 解x2(x-1)-(x-1)2-(x+3)(x-3) B.(-2x2)3=-8.x9 x3-x2-(x2-2+1)-(x2-9)=x3 x2-x+2x-1-x2+9=x3-3x2+2x+8, Cry片}r(≠0) 古x=2时,原式=名-子+1十 D.a2+2a2=3a 3.已知(a+b)2=49,a2+b=25,则ab=12. 867 8 素能·演练提升 1.设(2a十3b)2=(2a-3b)2+A,则A= A.12 B.±12 (D). C.6 D.±6 A.6ab B.12ab 3若m-品3则m+是=山, C.0 D.24ab 2.若关于x的二次三项式x2一a.x十36是一 4.已知a=7一3b,则代数式a2+6ab+9b的 个完全平方式,则a的值是(B). 值为49. 26
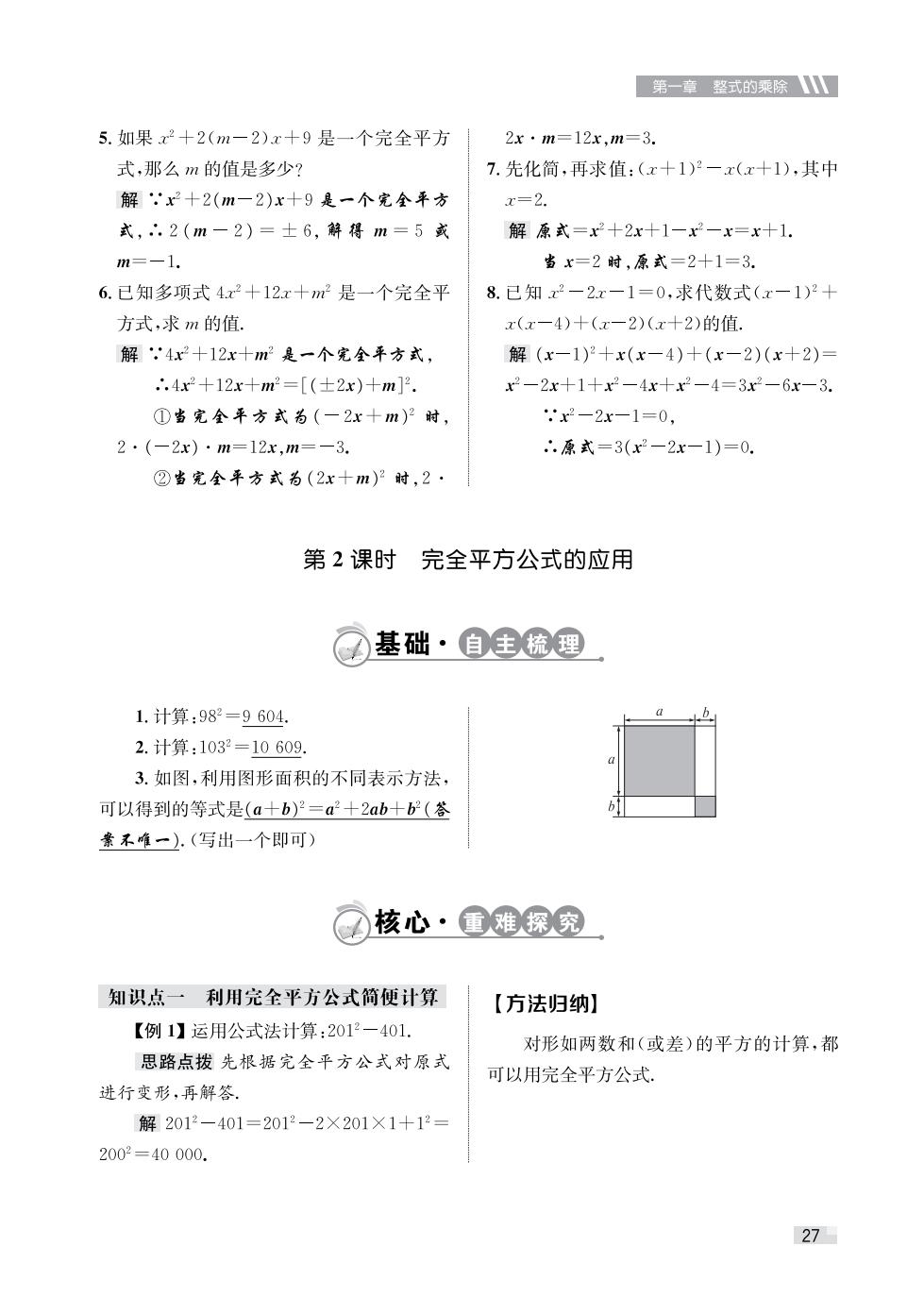
第一章整式的乘除、 5.如果x2+2(m一2)x+9是一个完全平方 2x·m=12x,m=3. 式,那么m的值是多少? 7.先化简,再求值:(x+1)2一x(x+1),其中 解.x2十2(m-2)x十9是一个完全平方 x=2. 式,.2(m-2)=士6,解得m=5或 解原式=x2+2x+1-x2-x=x十1. m=-1. 当x=2时,原式=2十1=3. 6.已知多项式4x2+12x十m2是一个完全平 8.已知x2-2x-1=0,求代数式(x-1)2十 方式,求m的值, x(x-4)十(x-2)(x十2)的值. 解,'4x2+12x十m2是一个完全平方式, 解(x-1)2+x(x-4)+(x-2)(x+2) ∴.4x2+12x+m2=[(士2x)+m]2. x2-2x+1+x2-4x+x2-4=3x2-6x-3. ①当完全年方式为(一2x十m)2时, .x2-2x-1=0, 2·(-2x)·m=12x,m=-3. .原式=3(x2-2x-1)=0. ②当完全平方式为(2x十m)时,2· 第2课时 完全平方公式的应用 基础·自主梳理 1.计算:982=9604. 2.计算:1032=10609 3.如图,利用图形面积的不同表示方法, 可以得到的等式是(a+b)2=a+2ab+b(答 素不唯一).(写出一个即可) Q核心·重难探究 知识点一利用完全平方公式简便计算 【方法归纳】 【例1】运用公式法计算:2012-401. 对形如两数和(或差)的平方的计算,都 思路点拨先根据完全平方公式对原式 可以用完全平方公式 进行变形,再解答, 解2012-401=2012-2×201×1+12 2002=40000. 27

儿家庭作业·数学·七年级,下册·配北师大版 知识点二利用完全平方公式解决实际 问题: 问题 若a+b=7,ab=5,求(a-b)2的值. 思路点拨解决这类问题通常是利用数 【例2】图①是一个长为2m、宽为2n的 形结合方法.(1)观察图形,可得小正方形的 长方形,沿图中虚线用剪刀将其均分成四个 小长方形,然后按图②的方式拼成一个正 边长;(2)根据完全平方公式,可得方法一;根 方形. 据完全平方公式的变形,可得方法二;(3)根 据同一图形的面积相等,可得答案;(4)根据 规律求解即可, 解(1)m-n. 图① 图② (2)(方法一)(m-n)2;(方法二)(m十n)2 (1)你认为图②中的阴影正方形的边长 Amn. 等于多少? (3)(十n)2一4mm=(m一n)(答案不唯一). (2)请用两种不同的方法表示图②中阴 (4)(a-b)2=(a+b)2-4ab=72-4× 影部分的面积 5=29. (3)观察图②,你能写出下列三个代数式 【方法归纳】 之间的等量关系吗? 代数式:(m十n)2,(m-n)2,4mm. 解决这类问题要数形结合,对几何图形 进行整体分析,利用面积相等求解. (4)根据(3)中的等量关系,解决下面的 新知·训练巩固 1.将边长为acm的正方形的边长增加4cm 3.已知三个圆的位置如图所示, 后,所得新正方形的面积比原正方形的面 其中m,n分别是两个较小圆的 积大(D). 直径,则图中阴影部分的面积 A.4a cm2 B.(4a+16)cm 为2m C.8a cm2 D.(8a+16)cm 2.如图,通过计算大正方形的面积,可以验证 4.运用完全平方公式计算: 一个等式,这个等式是(C) (1)63:(2)700.12:(3)499.9. 解(1)632=(60+3)2=602+2×60×3+ x xXyXz 32=3600+360+9=3969. y xy y yz (2)700.12=(700+0.1)2=7002+2× 2以2 700×0.1+0.12=490000+140+0.01= A.(x十y+z)2=x2+y2+x2+2y十xz+yz 490140.01. B.(x+y十z)2=x2+y2+x十2xy十xz十2yz (3)499.92=(500-0.1)2=5002-2× C.(x+y+x)2=x2+y+2+2xy十2xz十2yz 500×0.1+0.12=250000-100+0.01= D.(x十y+z)2=(x十y)2+2xz+2yz 249900.01. 28