
4、关于u的假设 ② 对u与X之间的关系进行假定一“均值独立性假设” 对于任何X值,我们都能在X值所描述的总体剖面上求出的期望(或平 均)值。关键假设是,u的平均值与X值无关。可把它写成: E(u x)=E(u) (2.6) 。 方程(26)表示,根据x值的不同把总体划分成若干部分,每 个部分中无法观测的因素都具有相同的平均值,而且这个共同 的平均值必然等于整个总体中山的平均值。 ·当方程(2.6)成立时,就说u的均值独立于X。 ·例如:教育与工资的关华中,能力会同时与教育和工资正相关, 2.6假设无论受教育程度如何,工人平均能力水平相同 中级计量经济学 16
4、关于u的假设 ② 对u与x之间的关系进行假定——“均值独立性假设” 对于任何x 值,我们都能在 x 值所描述的总体剖面上求出 u 的期望(或 平 均)值。关键假设是,u 的平均值与 x 值无关。 可把它写成: • E(u | x) = E(u) (2.6) • 方程(2.6)表示,根据 x 值的不同把总体划分成若干部分, 每 个部分中无法观测的因素都具有相同的平均值 ,而且这个共同 的平均值必然等于整个总体中 u 的平均值。 • 当方程(2.6)成立时,就说 u 的均值独立于x。 • 例如:教育与工资的关系中,能力会同时与教育和工资正相关, 2.6假设无论受教育程度如何,工人平均能力水平相同。 16 中级计量经济学

4、关于u的假设 ③ 当把均值独立性(2.6)与假设(2.5)相结合时,便得到零条件均值 假设(zero conditional mean assumption): E(u|x)=0 推导:E(ù|x)=E(u)=0 ·理解:X与其他因素不相关,X是随机分配的,等价于实验 数据的情形。 ·例如:教育与工资的关系中,能力会同时与教育和工资正相关,2.6 假设无论受教育程度如何,工人平均能力水平都相同,都为0。 ·例如:在施肥与产量的关系中,施肥量与土地质量和降雨量等其他因 素不相关。 >17 中级计量经济学
4、关于u的假设 ③ 当把均值独立性(2.6)与假设(2.5)相结合时,便得到零条件均值 假设 (zero conditional mean assumption): E(u | x) =0 推导:E(u | x) = E(u)=0 • 理解:x与其他因素不相关,x是随机分配的,等价于实验 数据的情形。 • 例如:教育与工资的关系中,能力会同时与教育和工资正相关,2.6 假设无论受教育程度如何,工人平均能力水平都相同,都为0。 • 例如:在施肥与产量的关系中,施肥量与土地质量和降雨量等其他因 素不相关。 17 中级计量经济学

4、关于u的假设 。如果u满足假设(2.6),X对y的影响就可以解释成因果 ·假设(2.6)能被满足吗?(经济逻辑和直觉;变量可观测性 和可度量性) ·教育与工资的例子 。施肥与产量的例子 ·真实世界中,零条件均值假设绝大多时候都无法成立。 因此需要计量方法来解决,当假设不满足的时候,怎样 获得因果关条 18 中级计量经济学
4、关于u的假设 • 如果u满足假设(2.6),x对y的影响就可以解释成因果 • 假设(2.6)能被满足吗?(经济逻辑和直觉;变量可观测性 和可度量性) • 教育与工资的例子 • 施肥与产量的例子 • 真实世界中,零条件均值假设绝大多时候都无法成立。 因此需要计量方法来解决,当假设不满足的时候,怎样 获得因果关系 18 中级计量经济学

,总体回归函数图形 Bonus:每个个体 的实际成绩的波 为什么要假设零条件均值? 动来源是什么? y=B。+B1x+u2.1) 对2.1取条件期望 EyX=B。+B,x+Eulx =B。+B1x E(vlx)=B+Bx ·EyX)是总体回归函数(PRF) ·是X的一个线性函数,y的均值如何随 着X的变化而变化。线性意味着X的1个单 位的变化,将使y的期望值改变B,° ·对应任何给定的X值,y的分布都以E(y|X) 图2-1作为x线性函数的E(yx) 为中心,例大学成绩与高中成绩的关系 19 中级计量经济学
总体回归函数图形 19 中级计量经济学 为什么要假设零条件均值? 𝒚 = 𝜷𝟎 + 𝜷𝟏 𝒙 + 𝒖 ( 2. 1) • 对2.1取条件期望 𝐄 𝒚 𝒙 = 𝜷𝟎 + 𝜷𝟏 𝒙 + 𝑬 𝒖 𝒙 = 𝜷𝟎 + 𝜷𝟏 𝒙 •E(y|x) 是总体回归函数(PRF) •是x的一个线性函数,y的均值如何随 着x的变化而变化。线性意味着x的1个单 位的变化,将使y的期望值改变𝜷𝟏 。 • 对应任何给定的x值,y的分布都以E(y|x) 为中心,例大学成绩与高中成绩的关系 Bonus:每个个体 的实际成绩的波 动来源是什么?
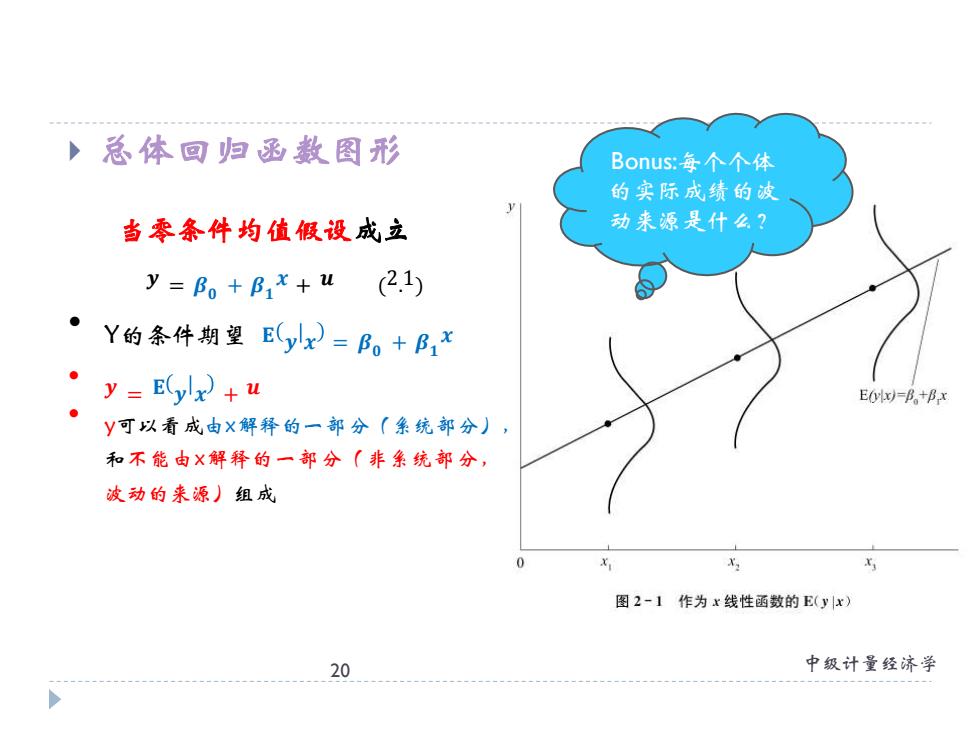
,总体回归函数图形 Bonus:每个个体 的实际成绩的波 当零条件均值假设成立 动来源是什么? y=B。+B1x+u2.1) ·Y的条件期望Eyx)=B。+Bx ·y=Ey+u E(ylx)=B+Bx y可以看成由×解释的一部分(系统部分), 和不能由X解释的一部分【非集统部分, 波动的来源)组成 图2-1作为x线性函数的E(yx) 20 中级计量经济学
总体回归函数图形 20 中级计量经济学 当零条件均值假设成立 𝒚 = 𝜷𝟎 + 𝜷𝟏 𝒙 + 𝒖 ( 2. 1) • Y的条件期望 𝐄 𝒚 𝒙 = 𝜷𝟎 + 𝜷𝟏 𝒙 • 𝒚 = 𝐄 𝒚 𝒙 + 𝒖 • y可以看成由x解释的一部分(系统部分), 和不能由x解释的一部分(非系统部分, 波动的来源)组成 Bonus:每个个体 的实际成绩的波 动来源是什么?