
辅助阅读材料 第四章光波的调制 第四章光波的调制 4.1光束的调制原理概述 激光是一种光频电磁波,具有良好的相干性,与无线电波相似。人们想利用 光来传递信息,往往会选择激光这样一种理想的光源。激光具有很高的频率 (105~105Hz),可供利用的频带宽度很宽,故传递信息的容量很大。 要用激光作为信息的载体,须解决如何将信息加载到激光上去的问题。这种 将信息加载于激光的过程称为调制,完成这一过程的器件装置称为调制器。其中 激光称为载波,起控制作用的低频信息称为调制信号。光波的电场强度为 E(t)=A.cos(@t+) (4.1) 式中A为振幅:为角频率;为相位角。既然光束具有振幅、频率、相位、强 度和偏振等参量,如果能够应用某种物理方法改变光波的这些参量之一,使其按 照调制信号的规律变化,那么激光束就受到了信号的调制,达到“运载”信息的 目的。 根据调制器与光源的关系,光调制可分为直接调制(内调制)和间接调制(外 调制)两大类(如图4.1、图4.2所示)。直接调制是指加载信号是在激光振荡 过程中进行的,以调制信号改变激光器的振荡参数,从而改变激光器输出特性以 实现调制。该方法主要用于半导体激光器(LD)和半导体发光二极管(LED) 两类光源,具体做法是把要传递的信息转变为电流信号注入LED或LD,从而获 得相应的光信号,采用的是电源调制方法。直接调制后的光波电场振幅的平方正 比例于调制信号,是对光强度实现调制。 电信号 光源→输出调制光 图4.1直接调制示意图 电信号 无深光信号,外南制器一输出误制光 图42间接调制示意图 1
辅助阅读材料 第四章 光波的调制 第四章 光波的调制 4.1 光束的调制原理概述 激光是一种光频电磁波,具有良好的相干性,与无线电波相似。人们想利用 光来传递信息,往往会选择激光这样一种理想的光源。激光具有很高的频率 (1013~1015Hz),可供利用的频带宽度很宽,故传递信息的容量很大。 要用激光作为信息的载体,须解决如何将信息加载到激光上去的问题。这种 将信息加载于激光的过程称为调制,完成这一过程的器件装置称为调制器。其中 激光称为载波,起控制作用的低频信息称为调制信号。光波的电场强度为 ( ) cos( ) c c c E t = A ω t +ϕ (4.1) 式中Ac为振幅;ωc为角频率;ϕc为相位角。既然光束具有振幅、频率、相位、强 度和偏振等参量,如果能够应用某种物理方法改变光波的这些参量之一,使其按 照调制信号的规律变化,那么激光束就受到了信号的调制,达到“运载”信息的 目的。 根据调制器与光源的关系,光调制可分为直接调制(内调制)和间接调制(外 调制)两大类(如图 4.1、图 4.2 所示)。直接调制是指加载信号是在激光振荡 过程中进行的,以调制信号改变激光器的振荡参数,从而改变激光器输出特性以 实现调制。该方法主要用于半导体激光器(LD)和半导体发光二极管(LED) 两类光源,具体做法是把要传递的信息转变为电流信号注入 LED 或 LD,从而获 得相应的光信号,采用的是电源调制方法。直接调制后的光波电场振幅的平方正 比例于调制信号,是对光强度实现调制。 图 4.1 直接调制示意图 图 4.2 间接调制示意图 1

辅助阅读材料 第四章光波的调制 间接调制是利用晶体的电光效应、磁光效应、声光效应等性质来实现对激光 辐射的调制,这种调制方式既适应于半导体激光器,也适应于其它类型的激光器。 间接调制是在激光形成以后加载调制信号。其具体方法是在激光器谐振腔外的光 路上放置调制器,在调制器上加调制电压,使调制器的某些物理待性发生相应的 变化,当激光通过它时,得到调制。 光源的调制方法及所利用的物理效应如表4.1所示。 表4.1光源的各种调制方法 调制 被调制的 调试法 所用的物理效应 方式 光场物理量 电光调制电光效应(一次电光效应、二次电光效应) 强度、相位 间接磁光调制 磁光效应(法拉第电磁偏转效应) 强度 调制 声光调制 声光效应(布喇格衍射效应) 强度 其它 电吸收效应、共振吸收效应等) 强度 直接 电源调制 强度 调制 采用不同的调制方法,可实现对光场的幅度、相位、频率和强度等物理量的 调制。 4.1.1振幅调制 振幅调制就是载波的振幅随调制信号的规律而变化的振荡,简称调幅。若调 制信号是一时间的余弦函数,即 a(t)=A.cos (4.2) 式中A.是调制信号的振幅,0.是调制信号的角频率。在进行激光振幅调制之后, 式(4.1)中的振幅A不再是常数,而是与调制信号成正比。调幅波的表达式为 E(1)=A.[1+ma cosor]cos(@t+e) (4.3) 利用三角函数将(4.3)式展开,得到调幅波的频谱公式 E()-A.cos(o+.)+A.cosl.+o.y+o.l+A.cos[(@.-@-Y+o.l (4.4) 式中m。=A./A.称为调幅系数。由上式可知,调幅波的频谱由三个频率成分组 成,第一项是载频分量,第二、三项是因调制产生的新分量,称为边频分量,如 2
辅助阅读材料 第四章 光波的调制 间接调制是利用晶体的电光效应、磁光效应、声光效应等性质来实现对激光 辐射的调制,这种调制方式既适应于半导体激光器,也适应于其它类型的激光器。 间接调制是在激光形成以后加载调制信号。其具体方法是在激光器谐振腔外的光 路上放置调制器,在调制器上加调制电压,使调制器的某些物理待性发生相应的 变化,当激光通过它时,得到调制。 光源的调制方法及所利用的物理效应如表 4.1 所示。 表 4.1 光源的各种调制方法 调制 方式 调试法 所用的物理效应 被调制的 光场物理量 电光调制 电光效应(一次电光效应、二次电光效应) 强度、相位 磁光调制 磁光效应(法拉第电磁偏转效应) 强度 声光调制 声光效应(布喇格衍射效应) 强度 间接 调制 其它 电吸收效应、共振吸收效应等) 强度 直接 调制 电源调制 强度 采用不同的调制方法,可实现对光场的幅度、相位、频率和强度等物理量的 调制。 4.1.1 振幅调制 振幅调制就是载波的振幅随调制信号的规律而变化的振荡,简称调幅。若调 制信号是一时间的余弦函数,即 a t A t m ω m ( ) = cos (4.2) 式中 Am 是调制信号的振幅,ω m 是调制信号的角频率。在进行激光振幅调制之后, 式(4.1)中的振幅 Ac 不再是常数,而是与调制信号成正比。调幅波的表达式为 ( ) [1 cos ]cos( ) c a m c c E t = A + m ω t ω t +ϕ (4.3) 利用三角函数将(4.3)式展开,得到调幅波的频谱公式 cos[( ) ] 2 cos[( ) ] 2 ( ) cos( ) c c m c a c c m c a c c c A t m A t m E t = A ω t +ϕ + ω +ω +ϕ + ω −ω +ϕ (4.4) 式中ma = Am Ac 称为调幅系数。由上式可知,调幅波的频谱由三个频率成分组 成,第一项是载频分量,第二、三项是因调制产生的新分量,称为边频分量,如 2

辅助阅读材料 第四章光波的调制 图3所示。上述分析是单余弦信号调制的情况。如果调制信号是一复杂的周期信 号,则调幅波的频谱将由载频分量和两个边频带组成。 4+。 2 图4.3调幅波的频谱图 4.1.2频率调制和相位调制 调频或调相就是光载波的频率或相位随着调制信号的变化规律而改变的振 荡。因为这两种调制波都表现为总相角()的变化,因此统称为角度调制。 对频率调制来说,就是式(4.1)中的角频率0.不再是常数,而是随调制信 号变化,即 o(t)=0。+△o()=0。+k,a(I) (4.5) 若调制信号仍为一余弦函数,则调制波的总相角为 w(t)=o()di+o=[o +k a(t)ldt+o=01+k a()dt+o (4.6) 则调制波的表达式为 E(t)=A。cos(o。1+m,sin1+p.) (4.7) 式中,k称为频率比例系数,m,=△o/on称为调频系数。 同样,相位调制就是(4.1)式中的相位角P随调制信号的变化规律而变化, 调相波的总相角为 y()=0.1+k。A cos01+p (4.8) 调相波的表达式为 E(t)=A.cos(@+k A cos@+) (4.9) 式中k。为相位比例系数 由于调频和调相实质上最终都是调制总相角,因此可写成统一的形式 E(t)=A.cos(@t+msin+) (4.10)
辅助阅读材料 第四章 光波的调制 图 3 所示。上述分析是单余弦信号调制的情况。如果调制信号是一复杂的周期信 号,则调幅波的频谱将由载频分量和两个边频带组成。 图 4.3 调幅波的频谱图 4.1.2 频率调制和相位调制 调频或调相就是光载波的频率或相位随着调制信号的变化规律而改变的振 荡。因为这两种调制波都表现为总相角ψ (t) 的变化,因此统称为角度调制。 对频率调制来说,就是式(4.1)中的角频率ωc 不再是常数,而是随调制信 号变化,即 (t) (t) k a(t) ω = ωc + ∆ω = ωc + f (4.5) 若调制信号仍为一余弦函数,则调制波的总相角为 c c f c c f c ψ t = ω t dt +ϕ = ω + k a t dt +ϕ = ω t + k a t dt +ϕ ∫ ∫ ∫ ( ) ( ) [ ( )] ( ) (4.6) 则调制波的表达式为 ( ) cos( sin ) c c f m c E t = A ω t + m ω t + ϕ (4.7) 式中,k f 称为频率比例系数,m f = ∆ω ω m 称为调频系数。 同样,相位调制就是(4.1)式中的相位角ϕ c 随调制信号的变化规律而变化, 调相波的总相角为 c m m c ψ (t) = ω t + kϕA cosω t +ϕ (4.8) 调相波的表达式为 ( ) cos( cos ) c c m m c E t = A ω t + kϕA ω t +ϕ (4.9) 式中kϕ为相位比例系数。 由于调频和调相实质上最终都是调制总相角,因此可写成统一的形式 ( ) cos( sin ) c c m c E t = A ω t + m ω t +ϕ (4.10) 3

辅助阅读材料 第四章光波的调制 将(4.10)式按三角公式展开,并应用 cos(msin.)=J,m)+22J2.m)cos(2no.) sin(msin.)=2∑Jn-m)sim2-lo.J 得到 E()=AJ(m)co)+A.J(mcos.+n+(-"cos(o.-n+.] (4.11ù 由此可见,在单频余弦波调制时,其角度调制波的频谱是由光载频与在它两 边对称分布的无穷多对边频组成。显然,若调制信号不是单频余弦波,则其频谱 将更为复杂。 4.1.3强度调制 强度调制是使光载波的强度(光强)随调制信号规律变化,如图4.4所示。光 束调制多采用强度调制形式,这是因为接收器一般都是直接响应其所接收的光强 变化。 光束强度定义为光波电场模的平方,其表达式为 1)-E2(0=Acos2(o1+p) (4.12) 强度调制的光强可表示为 I0-n+aocosa1+o) (4.13) 式中,k,为光强比例系数。仍设调制信号是单频余弦波,则有 I(t)+mcoso.lcos+) (4.14) 式中m。=k。A。,称为强度调制系数。强度调制波的须谱可用前面所提到的类似 方法分析,其结果与调幅波略有不同,其频谱分布除了载频及对称分布的两个边 频外,还有低频o和直流分量
辅助阅读材料 第四章 光波的调制 将(4.10)式按三角公式展开,并应用 ∑ ∞ = = + 1 0 2 cos( sin ) ( ) 2 ( ) cos(2 ) n m n m m ω t J m J m nω t ∑ ∞ = = − − 1 2 1 sin( sin ) 2 ( )sin[(2 1) ] n m n m m ω t J m n ω t 得到 ( ) ( ) cos( ) ( )[cos( ) ( 1) cos( ) ] 1 0 c m c n n c c c c n c m c E t = A J m ω t +ϕ + A ∑J m ω + nω t +ϕ + − ω − nω t +ϕ ∞ = (4.11) 由此可见,在单频余弦波调制时,其角度调制波的频谱是由光载频与在它两 边对称分布的无穷多对边频组成。显然,若调制信号不是单频余弦波,则其频谱 将更为复杂。 4.1.3 强度调制 强度调制是使光载波的强度(光强)随调制信号规律变化,如图 4.4 所示。光 束调制多采用强度调制形式,这是因为接收器一般都是直接响应其所接收的光强 变化。 光束强度定义为光波电场模的平方,其表达式为 ( ) ( ) cos ( ) 2 2 2 c c c I t = E t = A ω t + ϕ (4.12) 强度调制的光强可表示为 [1 ( )]cos ( ) 2 ( ) 2 2 p c c c k a t t A I t = + ω +ϕ (4.13) 式中,k p 为光强比例系数。仍设调制信号是单频余弦波,则有 [1 cos ]cos ( ) 2 ( ) 2 2 p m c c c m t t A I t = + ω ω +ϕ (4.14) 式中 ,称为强度调制系数。强度调制波的频谱可用前面所提到的类似 方法分析,其结果与调幅波略有不同,其频谱分布除了载频及对称分布的两个边 频外,还有低频 p p Am m = k ω m 和直流分量。 4
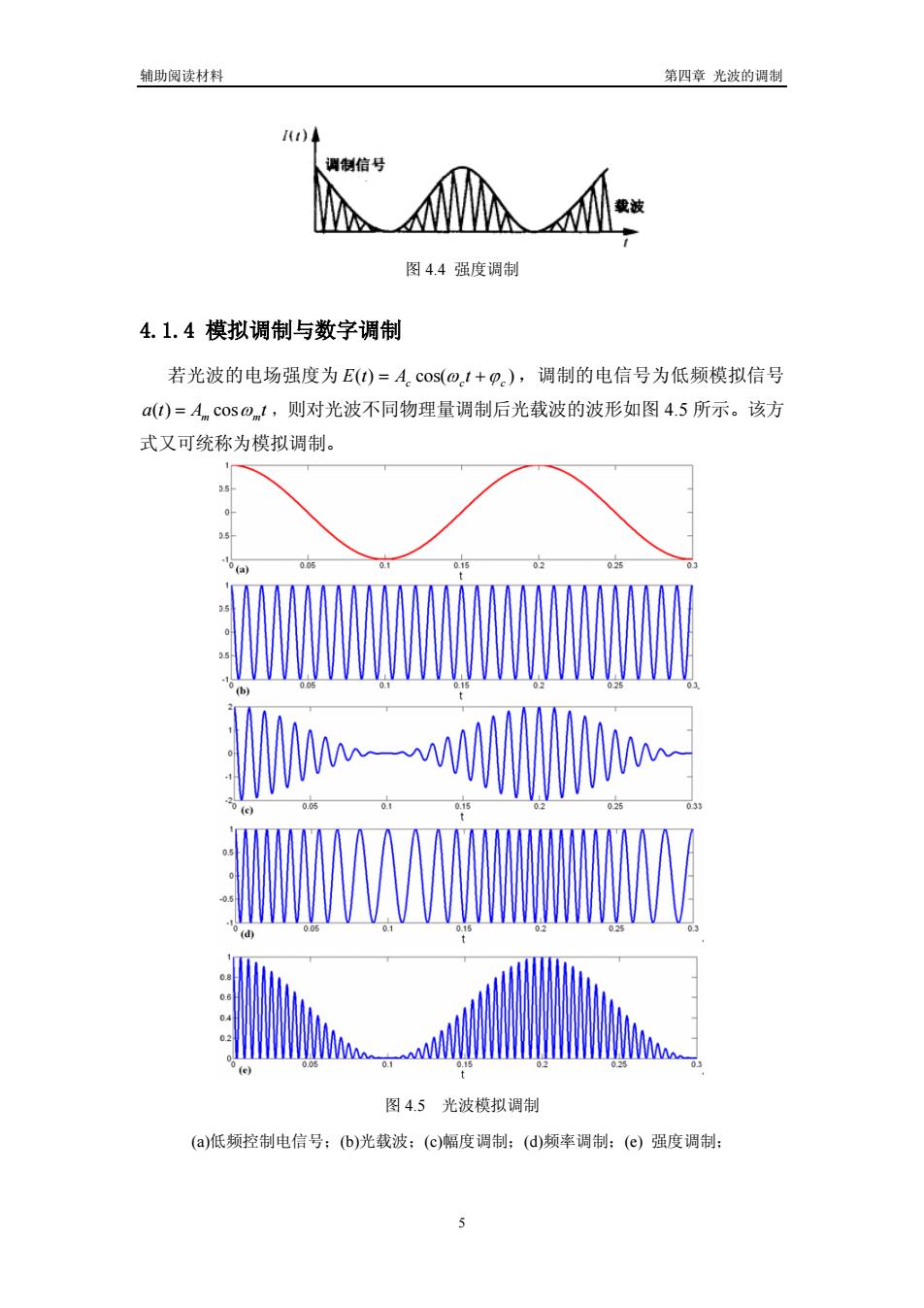
轴助阅读材料 第四章光波的调制 )4 调制信号 图4.4强度调制 4.1.4模拟调制与数字调制 若光波的电场强度为E()=A,cos(@,1+o),调制的电信号为低频模拟信号 a)=Acos),1,则对光波不同物理量调制后光载波的波形如图4.5所示。该方 式又可统称为模拟调制。 图45光波模拟调制 (a)低缬控制电信号:(b)光载波:(c)幅度调制:(d频率调制:(e)强度调制:
辅助阅读材料 第四章 光波的调制 图 4.4 强度调制 4.1.4 模拟调制与数字调制 若光波的电场强度为 ( ) cos( ) c c c E t = A ω t +ϕ ,调制的电信号为低频模拟信号 a t A t m ω m ( ) = cos ,则对光波不同物理量调制后光载波的波形如图 4.5 所示。该方 式又可统称为模拟调制。 图 4.5 光波模拟调制 (a)低频控制电信号;(b)光载波;(c)幅度调制;(d)频率调制;(e) 强度调制; 5