
第一章DVBT接收机中频率综合器性能 1.3基本概念一相位噪声和时钟抖动 频率综合器关系的性能指标有很多方面,而本论文主要的研究重点之一是噪声 的评估和优化,因此先介绍最重要的噪声指标相关的基本概念:相位噪声及时钟抖 动。 1.3.1相位噪声 顾名思义,相位噪声就是信号在相位上的噪声,带有相位噪声的信号可表示成 Asin(oot+中n)=A(cos中sin@ot+sind,coso,) (1-1) 其中Ao是信号的幅度;o是信号的中心频率,在通信系统中也称为载波频率;Φ 就是相位噪声。值得注意的是,相位噪声是个随机信号,它在时间上的均值是零, (1-1)式可以简化成: Asin(ot+pn)≈A(sin@ot-+中cos@t) (2) 可见,相位噪声的贡献只出现在载波的正交相位上,即coswot。 通常,噪声模型可以用频谱上的一系列不相关的、间隔为1Hz的正弦信号来表 示。假设频率综合器的输出可以表示成A。so,1,如果在中心频偏△o存在幅度为 an着加性噪声,则输出可以表示成 Ao sin@ot a,sin((@+Ao)t+) =A,sino,1+gsin(a,+△a)r+)+gsin(a。-△o)r-p) AM noise sina,+△or+p)-号sin(o,-Aor-p) (1-3) 2 PM noise 4 sin o+cos(△o1+))-sin/+号sin(Aoi+p)-cos& 2 可以看出,一个加性噪声对载波贡献两种类型的噪声:幅度调制(AM)噪声、相位调 制(PM)噪声。图1.5表示了在频谱上的幅度调制噪声和相位调制噪声的这种分解。 两种噪声的功率谱密度(PSD)是相等的,都是总噪声功率谱密度的一半。 0-A0,+A000。-A00+A0 幅度调制噪声 相位调制噪声 图1.5噪声的幅度调制和相位调制分解
第一章 DVB-T 接收机中频率综合器性能 1.3 基本概念-相位噪声和时钟抖动 频率综合器关系的性能指标有很多方面,而本论文主要的研究重点之一是噪声 的评估和优化,因此先介绍最重要的噪声指标相关的基本概念:相位噪声及时钟抖 动。 1.3.1 相位噪声 顾名思义,相位噪声就是信号在相位上的噪声,带有相位噪声的信号可表示成 0 0 0 0 0 sin( ) (cos sin sin cos ) A t n n A n ω + = φ φ ω t + φ ω t t (1-1) 其中A0是信号的幅度;ω0是信号的中心频率,在通信系统中也称为载波频率;Φn 就是相位噪声。值得注意的是,相位噪声是个随机信号,它在时间上的均值是零, (1-1)式可以简化成: 0 0 0 0 0 sin( ) (sin cos ) A t n A n ω + ≈ φ ω t +φ ω 0t (2) 可见,相位噪声的贡献只出现在载波的正交相位上,即cosω0t。 通常,噪声模型可以用频谱上的一系列不相关的、间隔为 1Hz的正弦信号来表 示。假设频率综合器的输出可以表示成 0 A sinω ,如果在中心频偏∆ω 存在幅度为 an着加性噪声,则输出可以表示成 0 0 0 0 0 0 0 AM 0 0 PM 0 sin sin(( ) ) sin sin(( ) ) sin(( - ) - ) 2 2 sin(( ) ) - sin(( - ) - ) 2 2 sin n n n noise n n noise A t a t a a A t t t a a t t A ω ω ω φ ω ω ω φ ω ω φ ω ω φ ω ω φ ω + + ∆ + = + + ∆ + + ∆ + + ∆ + ∆ = 144444444424444444443 1444444442444444443 0 0 cos( ) sin sin( ) cos 2 2 n n a a t t t t 0 + ∆ω + ⋅ φ ω + ∆ω + ⋅ φ ω t (1-3) 可以看出,一个加性噪声对载波贡献两种类型的噪声:幅度调制(AM)噪声、相位调 制(PM)噪声。图 1.5 表示了在频谱上的幅度调制噪声和相位调制噪声的这种分解。 两种噪声的功率谱密度(PSD)是相等的,都是总噪声功率谱密度的一半。 ω ω0 ω0 + ∆ω ω ω0 − ∆ω ω0 ω0 + ∆ω ω ω0 − ∆ω ω0 ω0 + ∆ω => + 幅度调制噪声 相位调制噪声 图 1.5 噪声的幅度调制和相位调制分解 7
复旦大学博士学位论文 如果噪声的功率谱密度是So以,则相位噪声的功率谱密度表示成[2] S(△o)= 1S(△o) (1-4) 2(△o)7 考虑到在频偏-△。处的噪声同样对相位噪声有贡献,则正负频偏处的噪声需要同时 考虑,这样得到的相位噪声与载波的比称之为单边带相位噪声,用C(4ω)表示: C(A0)= S,(△o)+S(-△o) (1-5) P 单位是dBc/Hz,其中P是在中心频率(载波)处的功率。例如,假设噪声是白噪声, Saw=No,则C(do=N/Pw)。 在实际电路中,单边带相位噪声的频谱如图1.6中所示。由于频率综合器的输出 往往是压控振荡器(VCO)的输出,所以图1.6(a)是自由VCO的相位噪声曲线,具有典 型的1/P、1/P和噪声基底(noise floor)区域;同时由于大多数频率综合器是基于锁相 环结构的,所以图1.6(b)给出了一种典型的经过锁相环输出的VCO相噪曲线,它的 区域包含1f、噪声平带、1/P和噪声基底区域。 C(o) C()】 11f 噪声平带 噪声基底 1/f2 噪声基底 (noise f1oor) (noise floor) (a)自由的VCO输出相位噪声 (b)基于PLL锁定的VCO输出相位噪声 图1.6VC0单边带相位噪声的谱密度 1.3.2时钟抖动 由于噪声是随机信号,随机信号需要用自相关函数R)和功率谱密度S)来表
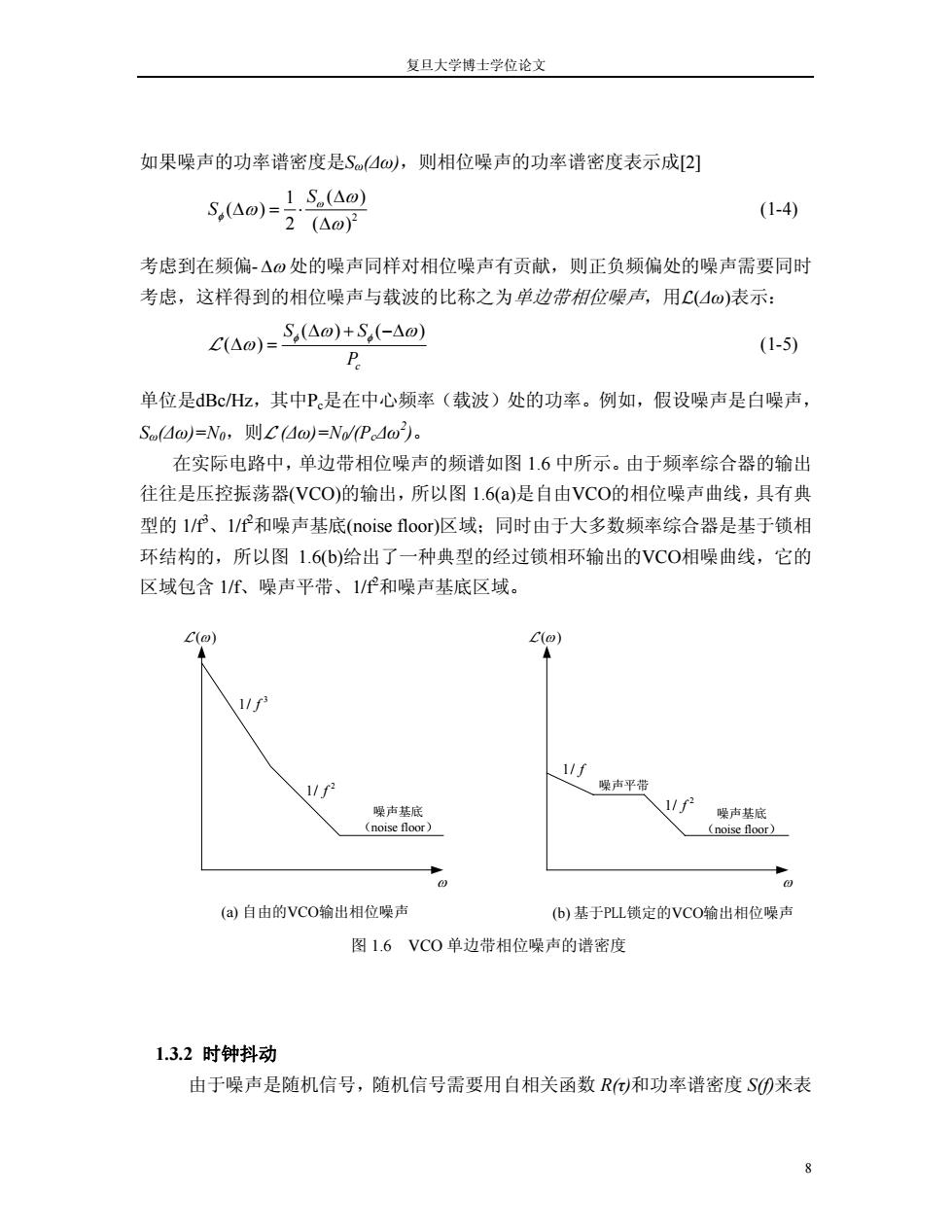
复旦大学博士学位论文 如果噪声的功率谱密度是Sω(∆ω),则相位噪声的功率谱密度表示成[2] 2 1 ( ( ) 2 ( ) S S ω φ ω) ω ω ∆ ∆ = ⋅ ∆ (1-4) 考虑到在频偏-∆ω 处的噪声同样对相位噪声有贡献,则正负频偏处的噪声需要同时 考虑,这样得到的相位噪声与载波的比称之为单边带相位噪声,用L(∆ω)表示: ( ) ( ( ) c S S P φ φ ω ω) ω ∆ + −∆ L ∆ = (1-5) 单位是dBc/Hz,其中Pc是在中心频率(载波)处的功率。例如,假设噪声是白噪声, Sω(∆ω)=N0,则L (∆ω)=N0/(Pc∆ω2 )。 在实际电路中,单边带相位噪声的频谱如图 1.6 中所示。由于频率综合器的输出 往往是压控振荡器(VCO)的输出,所以图 1.6(a)是自由VCO的相位噪声曲线,具有典 型的 1/f3 、1/f2 和噪声基底(noise floor)区域;同时由于大多数频率综合器是基于锁相 环结构的,所以图 1.6(b)给出了一种典型的经过锁相环输出的VCO相噪曲线,它的 区域包含 1/f、噪声平带、1/f2 和噪声基底区域。 2 1/ f 3 1/ f 1/ f L ( ) ω L ( ) ω ω ω (a) 自由的VCO输出相位噪声 (b) 基于PLL锁定的VCO输出相位噪声 噪声基底 (noise floor) 噪声基底 (noise floor) 2 1/ f 噪声平带 图 1.6 VCO 单边带相位噪声的谱密度 1.3.2 时钟抖动 由于噪声是随机信号,随机信号需要用自相关函数 R(τ)和功率谱密度 S(f)来表 8

第一章DVBT接收机中频率综合器性能 征,同时自相关函数和功率谱密度函数互为Fourier变换: R(t)←Fouer6m→S(f) 这个关系也被称为维纳-辛软Wiener-Khinchine)定理[3]。特别的,当r=0,并且当 随机信号的均值为零时,R)=σ,其中σ是随机信号的方差。对于相位噪声,此时 有: o2=∫S,f)d (1-6) 其中S0是相位噪声功率谱密度,σb是相位噪声的方差。 相位噪声在时钟系统中往往表现为时钟抖动(jitter),如图1.7所示。实际时钟 与理想时钟的边沿时间上的差值就是时钟抖动。时间上的差与对应的相位差的关 系表示为: A=T (1-7) 2π 同样时钟抖动也是随机信号,因此 (1-8) 其中σ,是时钟抖动的方差,T、w分别是时钟的周期和角频率。由(1-6)式,(1-8) 可以写成: S,(f)df (1-9) 0. 这个方程给出了时钟抖动与相位噪声的功率谱密度之间的关系。如果用单边带相 位噪声来表示,则(1-9)式可以进一步写成: aandr (1-10) 0 理想时钟 实际时钟 △Ln△Lnla+2△l+3 a4△L+5△n6△n+7 △Ln+g△n9△ln+0 时钟抖动 图17由相位噪声产生的时钟抖动 9
第一章 DVB-T 接收机中频率综合器性能 征,同时自相关函数和功率谱密度函数互为 Fourier 变换: Fourier Transform R(τ ) ←⎯⎯⎯⎯⎯→ S f ( ) 这个关系也被称为维纳-辛钦(Wiener-Khinchine)定理[3]。特别的,当τ=0,并且当 随机信号的均值为零时,R(τ)=σ 2 ,其中σ是随机信号的方差。对于相位噪声,此时 有: 2 S f ( )df σ φ φ +∞ −∞ = ∫ (1-6) 其中SΦ(f)是相位噪声功率谱密度,σΦ 2 是相位噪声的方差。 相位噪声在时钟系统中往往表现为时钟抖动(jitter),如图 1.7 所示。实际时钟 与理想时钟的边沿时间上的差值就是时钟抖动。时间上的差与对应的相位差的关 系表示为: 2 t T φ π ∆ ∆ = (1-7) 同样时钟抖动也是随机信号,因此 2 2 2 2 2 0 ( ) 2 t T φ φ σ σ σ π ω = = (1-8) 其中σt 2 是时钟抖动的方差,T、ω0分别是时钟的周期和角频率。由(1-6)式,(1-8) 可以写成: 2 2 0 1 ( ) t S f df σ φ ω +∞ −∞ = ∫ (1-9) 这个方程给出了时钟抖动与相位噪声的功率谱密度之间的关系。如果用单边带相 位噪声来表示,则(1-9)式可以进一步写成: 2 2 0 0 ( ) c t P σ f df ω +∞ = ∫ L (1-10) 时钟抖动 理想时钟 实际时钟 n ∆t n 1 t ∆ + n 2 t ∆ + n 3 t ∆ + n 4 t ∆ + n 5 t ∆ + n 6 t ∆ + n 7 t ∆ + n 8 t ∆ + n 9 t ∆ + n 10 t ∆ + ... ... 图 1.7 由相位噪声产生的时钟抖动 9
复旦大学博士学位论文 从(1-10)可以看出,时钟抖动实际上是相位噪声在频率域上的积分,因此不同的 相位噪声曲线可能具有相同的时钟抖动。从图1.8可以知道,即使()和(b)相位噪声 曲线不同,只要有相同的积分,它们就有着相同的jitter。这一点在一些对电磁兼容 和泄漏有特殊要求的系统中特别重要,图1.8(b)的相位噪声曲线可以避免在中心频 率附近泄漏出额外的电磁能量。但是另一方面,在无线通信系统接收电路中,图1.8() 的相位噪声则有着更好的性能。因此根据不同的系统性能要求,需要选择的相位噪 声曲线也不相同。 C(f) C(f) (a) (b) 图1.8具有相同时钟抖动的两种不同相位噪声曲线 1.4DVB-T接收机中频率综合器的性能估算 1.4.1理想OFDM信号的表示 假设在发送端和接收端采用N点的DFT算法进行信号的调制和解调,则在信号 中存在了N个载波,即使在这些载波中有一些是用来提供保护边带的零,但是这些 载波事实上还是存在的,所以发送的信号可以表示成: N-1 s)=∑S,eot+tau (1-11) 其中,S是经过QPSK或QAM调制的复信号: o是子载波间距,即oU=2π/T: o0是载波中心频率。 10
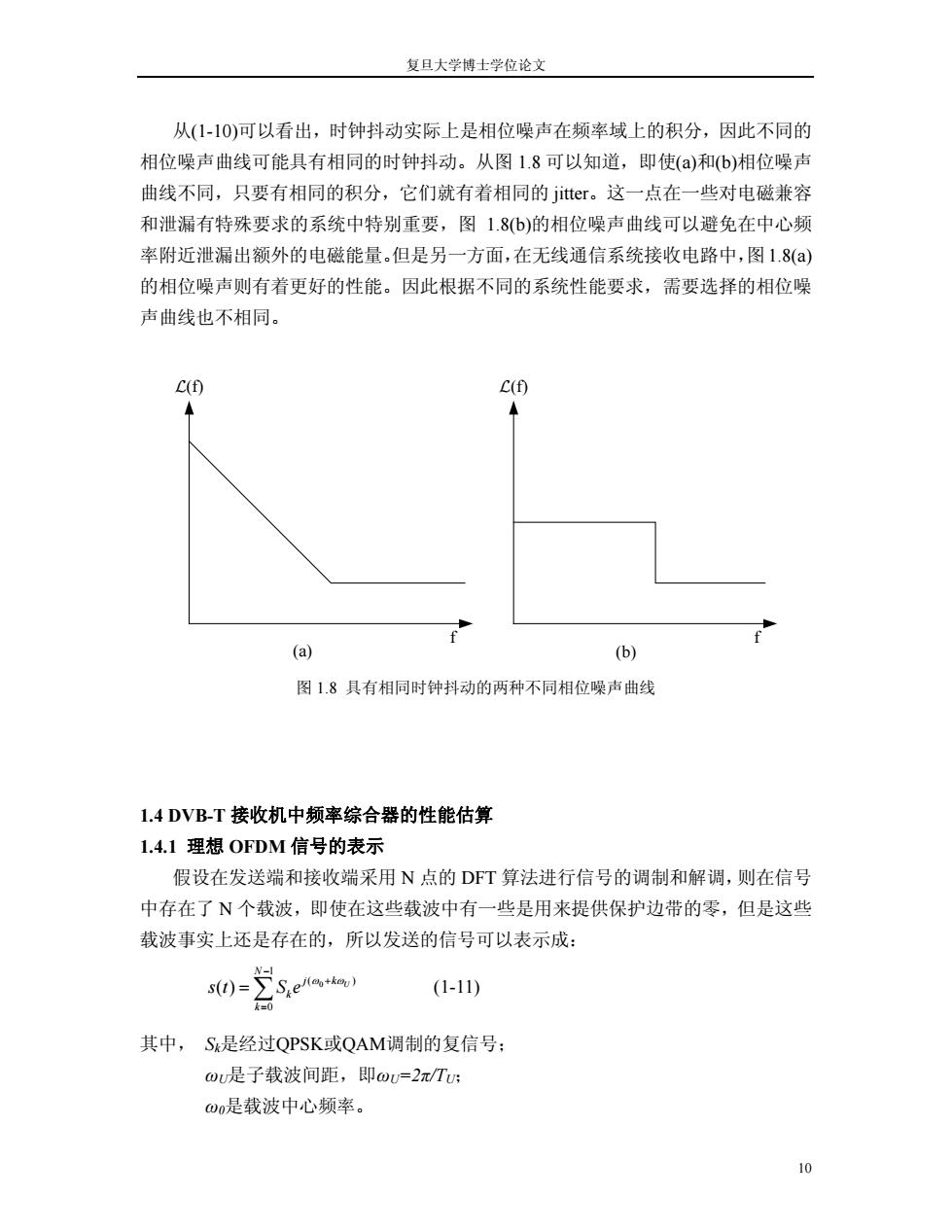
复旦大学博士学位论文 从(1-10)可以看出,时钟抖动实际上是相位噪声在频率域上的积分,因此不同的 相位噪声曲线可能具有相同的时钟抖动。从图 1.8 可以知道,即使(a)和(b)相位噪声 曲线不同,只要有相同的积分,它们就有着相同的 jitter。这一点在一些对电磁兼容 和泄漏有特殊要求的系统中特别重要,图 1.8(b)的相位噪声曲线可以避免在中心频 率附近泄漏出额外的电磁能量。但是另一方面,在无线通信系统接收电路中,图1.8(a) 的相位噪声则有着更好的性能。因此根据不同的系统性能要求,需要选择的相位噪 声曲线也不相同。 L(f) L(f) f f (a) (b) 图 1.8 具有相同时钟抖动的两种不同相位噪声曲线 1.4 DVB-T 接收机中频率综合器的性能估算 1.4.1 理想 OFDM 信号的表示 假设在发送端和接收端采用 N 点的 DFT 算法进行信号的调制和解调,则在信号 中存在了 N 个载波,即使在这些载波中有一些是用来提供保护边带的零,但是这些 载波事实上还是存在的,所以发送的信号可以表示成: 0 1 ( 0 ( ) U N j k k k s t S e ω ω − + = = ∑ ) (1-11) 其中, Sk是经过QPSK或QAM调制的复信号; ωU是子载波间距,即ωU=2π/TU; ω0是载波中心频率。 10

第一章DVBT接收机中频率综合器性能 经过单位冲击响应为h)的信道传输后,理想接收信号r)可以表示成: ()H,S, Rea (1-12) (so k=0 其中,H是信道在第k个子载波上的复频域响应,与时域响应(t)相对应:R是理想 接收信号在第k个子载波上复幅度。如果经过理想本地振荡器(LO)的下混频,得到信 号是: W-1 0=2Re (1-13) 假设接收的信号是非周期的,且只在[0,T]时间段内有效,其他时间段为0,则信号 的Fourier?变换是: x,=手0eh= Reu-awd=·R (1-14) 0k=0 1.4.2相位噪声对OFDM接收信号的影响 在实际的接收过程中,由于LO存在着相位噪声,则接收到的OFDM基带信号 是: N-I x)=eoo∑Rer (1-15) 其中p)是相位噪声,因此: (1-16) 由于)是均值为零的随机信号,上式可以简化成: x,=于0+pe吃R.cw-w'd N-1 (1-17) =T7[R+j∑R0] 其中 m= (t)emdt (1-18) 11
第一章 DVB-T 接收机中频率综合器性能 经过单位冲击响应为 h(t)的信道传输后,理想接收信号 r(t)可以表示成: (1-12) 0 1 1 ( ) ( 0 0 ( ) U N N j k t j k t k k k k k r t H S e R e ω ω ω ω − − + = = = ∑ = ∑ 0 ) + U U l 其中,Hk是信道在第k个子载波上的复频域响应,与时域响应h(t)相对应;Rk是理想 接收信号在第k个子载波上复幅度。如果经过理想本地振荡器(LO)的下混频,得到信 号是: (1-13) 1 0 ( ) U N jk t k x t R e ω − = ∑ 假设接收的信号是非周期的,且只在[0,TU]时间段内有效,其他时间段为 0,则信号 的Fourier变换是: 1 ( ) 0 0 0 ( ) U U U U T T N jl t j l k t l k k X x t e dt R e dt T R ω ω − − − − = = = ∑ = ∫ ∫ ⋅ U k (1-14) 1.4.2 相位噪声对 OFDM 接收信号的影响 在实际的接收过程中,由于 LO 存在着相位噪声,则接收到的 OFDM 基带信号 是: (1-15) 1 ' ( ) 0 ( ) U N j t jk t k x t e R e ϕ ω − = ∑ 其中 φ(t)是相位噪声,因此: 1 ' ' ( ) ( ) 0 0 0 ( ) U U U T T N jl t j t j l k t l k X x t e dt e R e dt ω ϕ − − = = = ∫ ∫ ∑ − − ω (1-16) 由于 φ(t)是均值为零的随机信号,上式可以简化成: 1 ' ( ) 0 0 1 1 ( ) ( ) 0 0 0 0 1 0 (1 ( )) = ( ) = [ ] U U U U U U T N j l k t l k k T T N N j l k t j l k t k k k k N U l k l k k X j t R e dt R e dt j R t e T R j R ω ω ω ϕ ϕ ϕ − − − = − − − − − − = = − − = = + + + ∫ ∑ ∫ ∑ ∑ ∫ ∑ dt (1-17) 其中 0 1 ( ) U U T jm t m U t e dt T ω ϕ ϕ − = ∫ (1-18) 11