
如果将t改变为t/a,其巾a为正的常数,则函数f(t)将变成f(t/a)。如果我们用F(s》表 示f(t)的拉普拉斯变换,则f(t,'a)的拉普拉斯变换可以求得如下: [r(&)])e 令t/a=t1利as=1.得到 [()}门=feda,) =ef4e山, -aF(51) 即 [f(&)]=aFa) | 作为例子,考虑f(t)=e‘和f(t/5)=eoa,这时得到 [0]-2[e]=广 因此 [(号)]=y[e]-5F5s)-点 通过对e“直接求拉普拉斯变换,可以容易地证明上述结果: [e]=1 5 s+0.2=55十1 2.3.12关于拉普拉斯积分下限的说明 在某些情况下,f()在t=0处有一个脉冲函数。这时必须明确地指出拉普拉斯积分的下 限是0一还是0十,因为对于这两种下限,f()的拉普拉斯变换是不同的。如果拉普拉斯积分 下限的这种区别是必要的,可采用下列符号予以区分: g,[f]=fee y[fe]=fwedt=g[re1+feed 如果f(t)在t=0处包含一个脉冲函数,则 9+[f(t)]≠9-[f()] 因为在这种情况下 foe业≠0 显然,如果在t=0处f()不具有脉冲函数(即如果被变换的函数在t=0一和t=0+之间是有 限的),则有 9+[f(t)]=E[f(t)] 2.4拉普拉斯变换定理 本节将介绍几个拉普拉斯变换定理,它们在控制工程中是很重要的。 ·19·
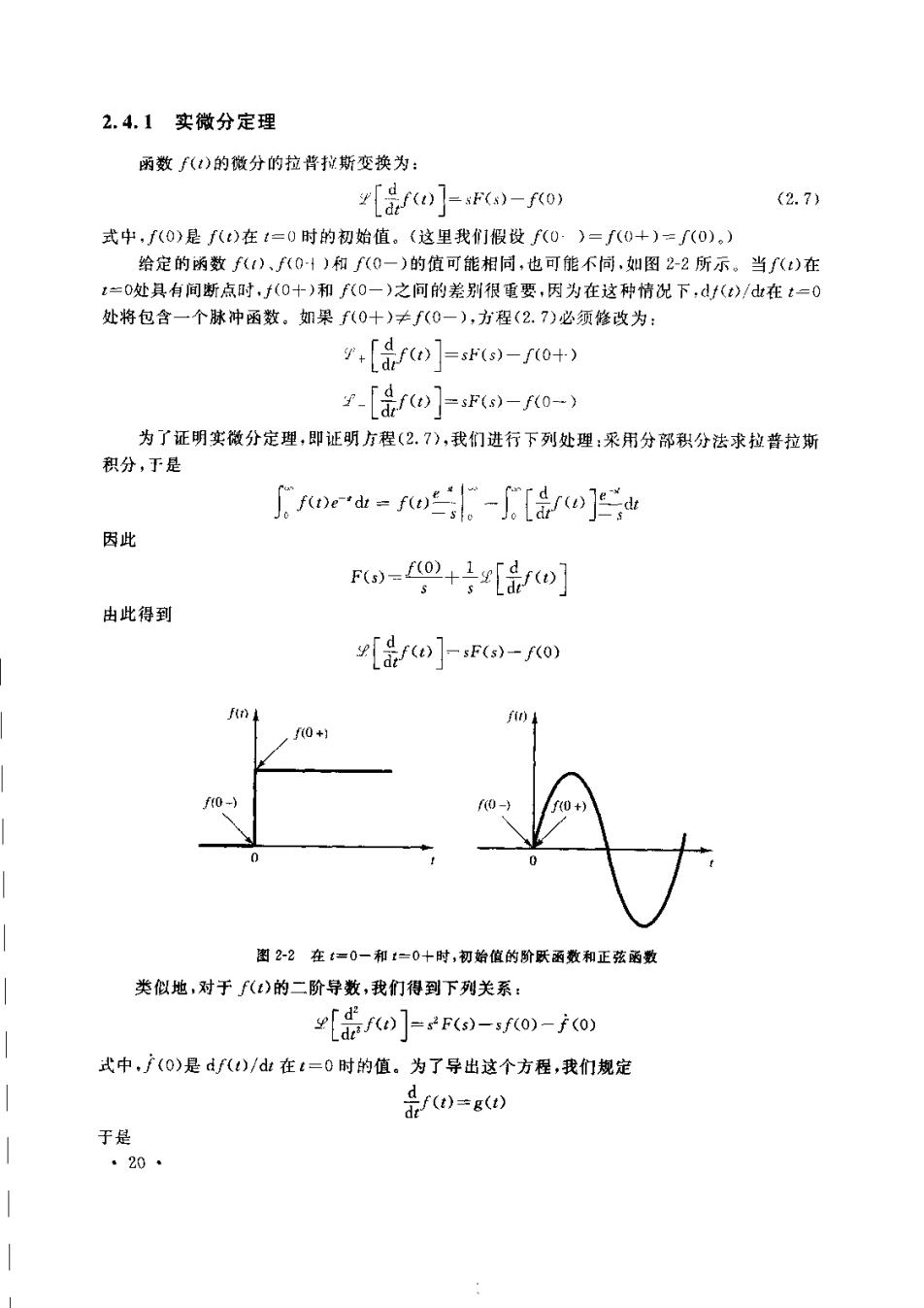
2.4.1实微分定理 函数f(t)的微分的拉普拉斯变换为: -o-Ro (2.7) 式中,f(0)是f(t)在t=0时的初始值。(这里我们假设f(0·)=f(0+)=f(0)。) 给定的函数f(1、(01)和f(0一)的值可能相同,也可能不同,如图2-2所示。当f()在 t=0处具有间断点时,f(0十)和f(0一)之间的差别很重要,因为在这种情况下,df(t)/dt在t=0 处将包含一个脉冲函数。如果f(0十)≠f(0一),方程(2.7)必须修改为: :[品]=s(s)-o+) -[是fw]sFs)-f0-) 为了证明实微分定理,即证明方程(2.7),我们进行下列处理:采用分部积分法求拉普拉斯 积分,于是 0fed业=f-[/e] 因此 Fo0-o+[新o] 由此得到 [品fe]-ss)-fo) f0+ f0-) f0-) + 图22在t=0一和1一0十时,初始值的阶跃函数和正弦函数 类似地,对于f(t)的二阶导数,我们得到下列关系: 9[0]=rFe-0)-K0) 式中,f(0)是d()/dt在t=0时的值。为了导出这个方程,我们规定 F0=g@0 于是 ·20·

[需fe]-[品ge]=s[go]-go) -sdfo]-f(o =s2F(s)-sf(0)-f(0) 类似地,对于f(t)的n阶导数,我们得到 可f]=sF-gf0)-gj0)-…-r6)-f 式中,f(0),f(0),,f0)分别代表f(t),df(z)/dt,…,d-f(t)/dr1在t=0时的值。如果 有必要区分坐+和-,可以根据究竞是要求Y,还是出-,而相应地将t=0+或t=0一代进 f(t),df(t)/de,…,d"-1f(t)/dt"-。 应当指出,为了保证f(t)的各阶导数的拉普斯变换存在,df(t)/d(n=1,2,3,…)必须 是可以进行拉普拉斯变换的。 还应当指出,如果f(t)及其各阶导数的所有初始值全都等于零,则f(t)的n阶导数的拉 普拉斯变换为sF(s)。 例2.1考忠下列余弦函数: g(t)=0, KO =cOSO t20 该余弦函数的拉普拉斯变换可以像前面讨论过的求正弦函数的拉普拉斯变换那样直接求出, 但是这里我们通过正弦函数的拉普拉斯变换导出余弦函数的拉普拉斯变换,说明实微分定理 的应用。如果规定 f(t)=0, t<0 =sinot, t≥0 则 9[sinQt]-F(s)- 余弦函数的拉普拉斯变换可以求得如下: Lcoswt]-dsinwt]-[sF()-f(0)] =[w-o]=a 2.4.2终值定理 终值定理表示了f(t)的稳态值与sF(s》在s=0点附近的状态之间的关系。显然,当且仪 当imf(t)存在时(这意味着当t→o∞时,f(t)将稳定到确定值),才能应用该定理。如果sF(s) 的所有极点位于左半s平面,则lif(t)存在。但是,如果sF(s)有极点位于虚轴或位于右半s 平面内,f(t)将分别包含振荡的或按指数规律增长的时间函数,因而limf(t)将不存在。如果 ·21·

f(t)是E弦函数sinot,sF(s)将有位于虚轴上的极点s一士jw,因此]inmf(t)不存在,所以终值 定理不适用于这类函数。 终值定理可以陈述知下:如果f(t)和df(t)/d!是可以进行拉普拉斯变换的,F(s)是f() 的拉普拉斯变换,并且imf(t)存在,则有 limf(t)-limsF(s) 为了证明该定理,我们在f八1)的导数的拉普拉斯变换方程中,令s趋近于零,即 imf[是fo]kat-im[Fs)o】 因为lime=1,所以得到 rJd)-o =limsF (s)-f(0) 由此得到 f()=limf(t)=limsF(s) 终值定理表明,f(t)的稳态值与s=0附近的sF(s)的值相同。因此,f()在t=oo时的值 可以直接从F(s)得到。 例2.2已知 4[f)]=F()=(5+j 1 试求imf(t)。 因为sF(s)=1/(s+1)的极点位于左半s平面内,所以1imf(t)存在。因此,在这种情况下 可以应用终值定理: 1 imf)=foo)=imsF()=:g十i-in中7=1 实际上,这个结果可以容易地得到证明,因为 f(t)=1-e-, ≥0 2.4.3初值定理 初值定理是终值定理的对偶定理。利用这个定理,我们可以从f(t)的拉普拉斯变换直接 求出f(t)在t=0十时的值。初值定理不能给出严格的t=0时的f(:)值,但是能够给出时间 路大于零时(t)的值。 初值定理陈述如下:如果f(t)和df(t)/dt均为可以进行拉普拉斯变换的,并且imsF(s) 存在,则有 f(0+)=limsF(s) 为了证明这个定理,我们利用df(t)/dt的出+变换方程,即 [f]=F()-f0+) ·22·

对于时间间隔0十≤≤∞,当s趋近于无穷大时,e趋近于零(注意,由于存在此条件,必 须采用9,,而不采用Y)。因此, 4[d=mF0-o+门-0 即 f(0)=lims(s) 在应用初值定理时,我们对sF(s)的极点位置不加限制。因此,对于正弦函数,初值定理 是成立的。 应当指出,初值定理和终值定理提供了·种简使的对解答的检查方法,因为它们使得不把 5的函数变成时问函数的情况下,也能够预测系统的时域性能。 2.4.4实积分定理 如果f(t)是指数级的,并且f(0一)=f(0+)=f(0),则f()d的拉普拉斯变换存在,并 且求得为: y[red]-9+'o2 (2.8) 式中,(s)=[f()],而1(0)=f(t)d是在t=0时的值。 应当指出,如果f(t)在t=0处包含一个脉冲函数,则f1(0十)≠1(0一)。因此,如果 f(t)在t=0处包含一个脉冲函数,必须将方程(2.8)进行如下修正: 2+[r0]-+o+) 5 -rod ]-0- 由方程(2.8)给出的实积分定理可证明如下。 应用分部积分法进行积分,得到 d]-oda =frew业]r-fok =rea.+0fewe*山 =0)+F( 即证明了定理。 可以看出,在时域中的积分被转变成在5域中相除。如果积分的初值为零,则(t)积分的 拉普拉斯变换为F(s)/s。 当需要涉及f(t)的定积分时,可以将方程(2.8)给出的实积分定理做些许修改。如果 f(t)是指数级的,则定积分 「f(1)dk的拉普拉斯变换可由下式确定: ·23·