
(2)粒子的最小能量不等于零 最小能量E= n2h2 2ma 也称为基态能或零点能。 零点能的存在与不确定度关系协调一致。 上美不家返可退此
上页 下页 返回 退出 (2)粒子的最小能量不等于零 最小能量 也称为基态能或零点能。 零点能的存在与不确定度关系协调一致。 2 2 1 2 2 n E ma =
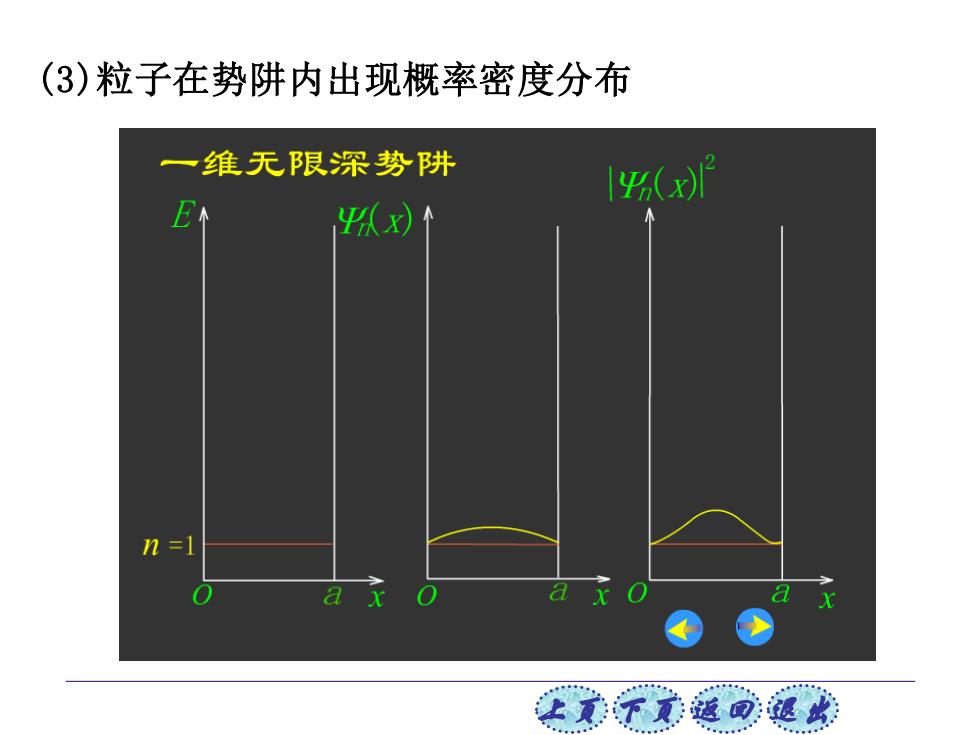
(3)粒子在势阱内出现概率密度分布 一维无限深势阱 x E 队个 n=1 让美下觉返司速此
上页 下页 返回 退出 (3)粒子在势阱内出现概率密度分布
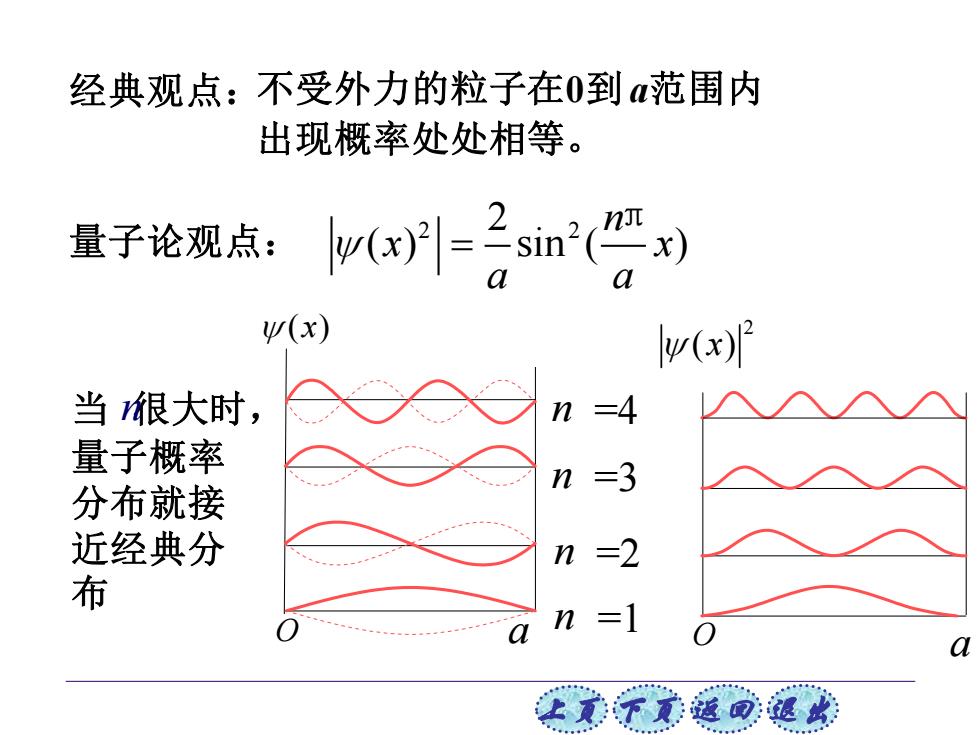
经典观点:不受外力的粒子在0到范围内 出现概率处处相等。 量子论观点: 2sin') w(x) (x) 当很大时, n =4 量子概率 n =3 分布就接 近经典分 n =2 布 n =1 a 上意子意返回退此
上页 下页 返回 退出 不受外力的粒子在0到a范围内 出现概率处处相等。 量子论观点: 经典观点: 2 2 2 ( ) sin ( ) n x x a a = π a O a =1 =2 =3 n =4 n n n O 当 很大时, 量子概率 分布就接 近经典分 布 n ( ) x 2 ( ) x
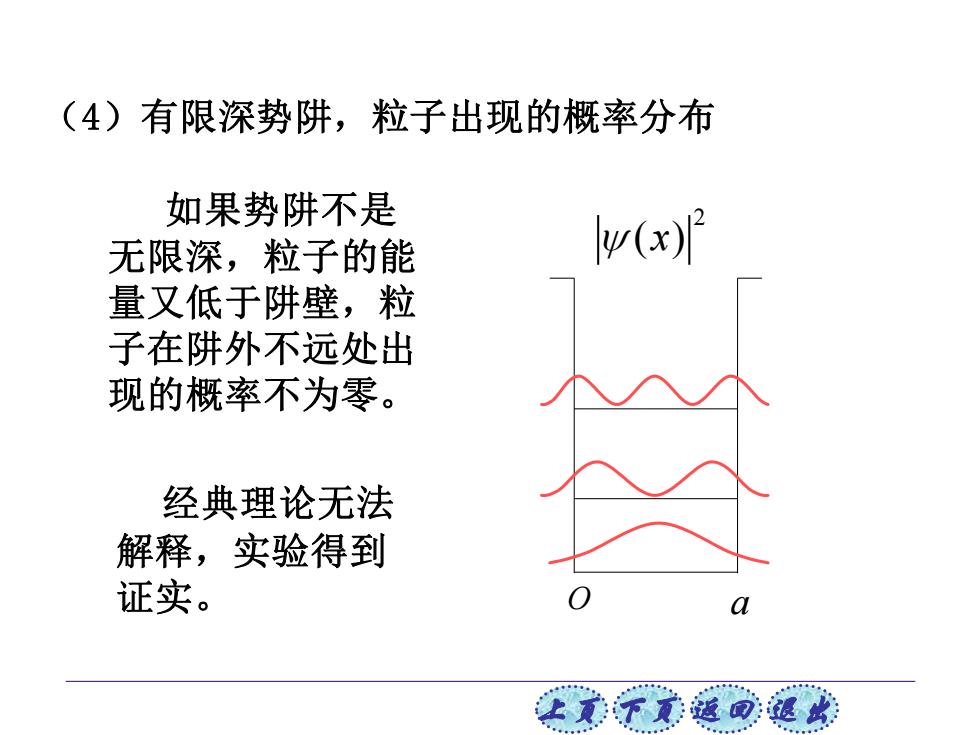
(4)有限深势阱,粒子出现的概率分布 如果势阱不是 无限深,粒子的能 w(x) 量又低于阱壁,粒 子在阱外不远处出 现的概率不为零。 经典理论无法 解释,实验得到 证实。 让美下觉返同速
上页 下页 返回 退出 (4)有限深势阱,粒子出现的概率分布 如果势阱不是 无限深,粒子的能 量又低于阱壁,粒 子在阱外不远处出 现的概率不为零。 经典理论无法 解释,实验得到 证实。 O a 2 ( ) x