
§13-5德布罗意波微观粒子的波粒二象性 一、德布罗意波 光的干涉、衍射等现象证实了光的波动性;热辐 射、光电效应和康普顿效应等现象又证实了光的粒子 性。光具有波粒二象性。 德布罗意波在光的二象性的启发下,提出了与光 的二象性完全对称的设想,即实物粒子(如电子、质 子等)也具有波粒二象性的假设。 质量为的粒子以速度匀速运动时,具有能量E 和动量P;从波动性方面来看,它具有波长和频率2 些量之间的关系遵从下述公式:
上页 下页 返回 退出 光的干涉、衍射等现象证实了光的波动性;热辐 射、光电效应和康普顿效应等现象又证实了光的粒子 性。光具有波粒二象性。 德布罗意波在光的二象性的启发下,提出了与光 的二象性完全对称的设想,即实物粒子(如电子、质 子等)也具有波粒二象性的假设。 一、德布罗意波 §13-5 德布罗意波 微观粒子的波粒二象性 质量为 的粒子以速度 匀速运动时,具有能量 和动量 ;从波动性方面来看,它具有波长 和频率 , 这 些量之间的关系遵从下述公式: m v E p n

h E=mc2=hv p=mv= 具有静止质量的实物粒子以速度 运动,则 和该粒子相联系的平面单色波的波长为 德布罗意 hhh 公式 = mv mov V h 如果v<女那么= mov 让美觉返司退
上页 下页 返回 退出 具有静止质量 的实物粒子以速度 运动,则 和该粒子相联系的平面单色波的波长为 m0 v 2 2 0 1 h h h v p mv m v c = = = − 德布罗意 公式 2 E mc h = = h p mv = = 0 h m v 如果 v c ,那么 =

德布罗意认为电子的物质波绕圆轨道传播时, 只有满足驻波条件时,此轨道才是稳定的。在这一 假设下,可以得出玻尔假设中的有关电子轨道角动 量量子化条件: 2r=nλn=1,2,3,. h λ= mv h myr =n n=1,2,3,. 2元 让贰子家适回退此
上页 下页 返回 退出 德布罗意认为电子的物质波绕圆轨道传播时, 只有满足驻波条件时,此轨道才是稳定的。在这一 假设下,可以得出玻尔假设中的有关电子轨道角动 量量子化条件: 2 1 πr n n = = ,2 3, h mv = 1 2 3 2π h mvr n n = =
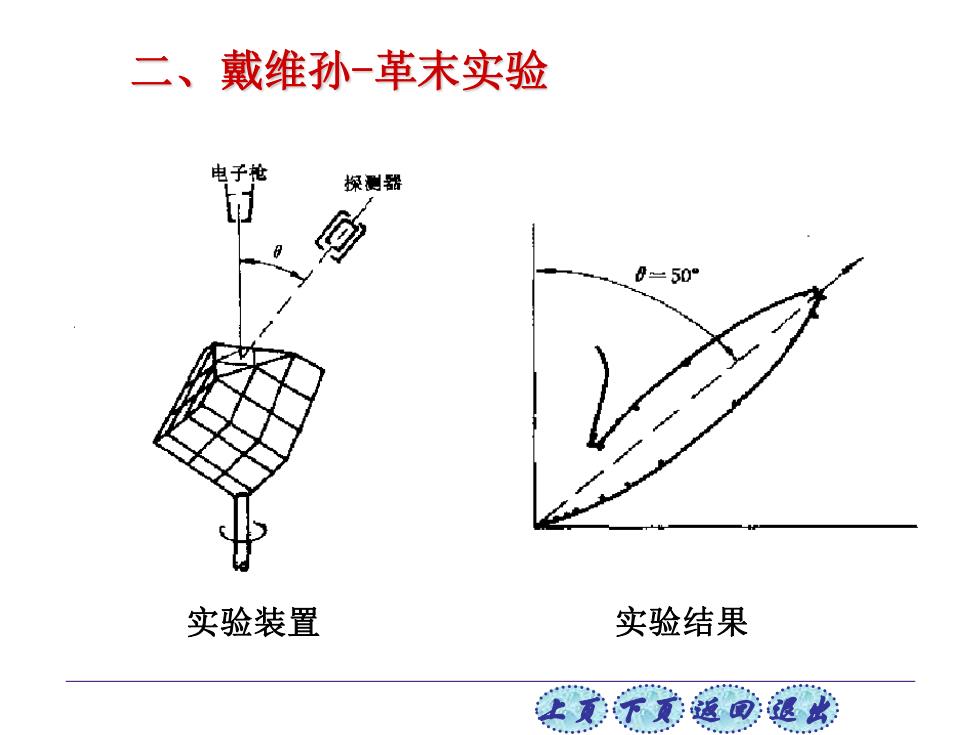
二、戴维孙-革末实验 电子 探测器 0=50 实验装置 实验结果 让美觉返司退
上页 下页 返回 退出 实验装置 实验结果 二、戴维孙-革末实验
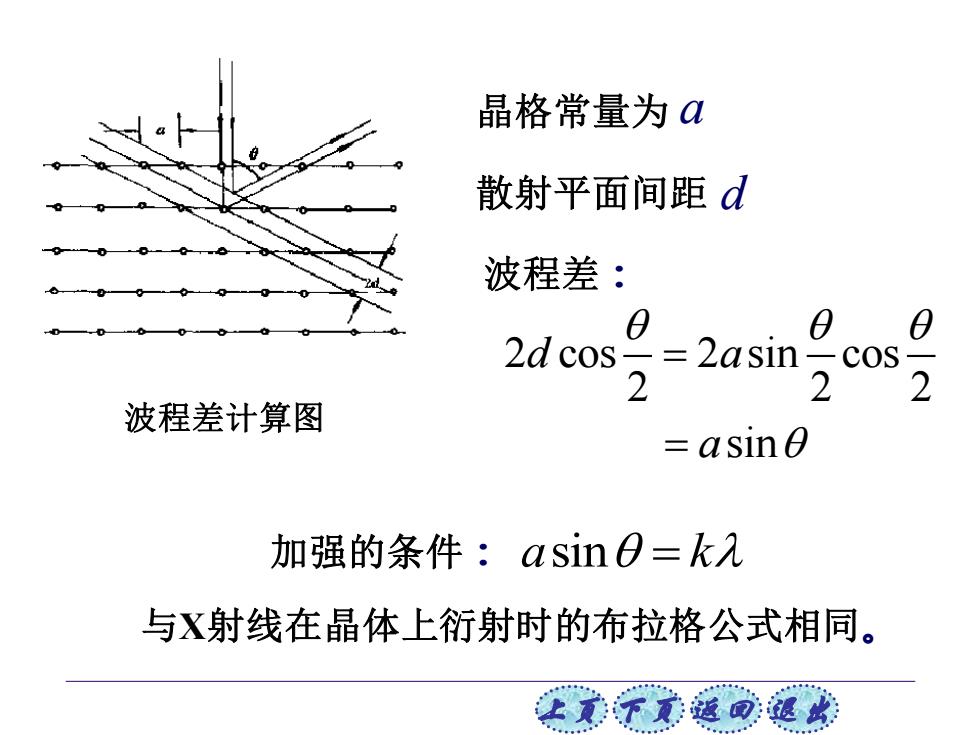
晶格常量为☑ 散射平面间距d 波程差: 0 0 2d cos=2asincos 2 2 2 波程差计算图 asin O 加强的条件:asin0=k入 与X射线在晶体上衍射时的布拉格公式相同。 让贰下觉返回退此
上页 下页 返回 退出 晶格常量为 a 散射平面间距 d 波程差: 加强的条件: 波程差计算图 与X射线在晶体上衍射时的布拉格公式相同。 2 cos 2 sin cos 2 2 2 sin d a a = = a k sin =