§13-6不确定关系 电子衍射 观察目镜 1927年海森伯(W.Heisenberg)分析了几个理 想实验后提出了不确定关系。 化贰不元通回退欢
上页 下页 返回 退出 1927年海森伯(W.Heisenberg)分析了几个理 想实验后提出了不确定关系。 §13-6 不确定关系
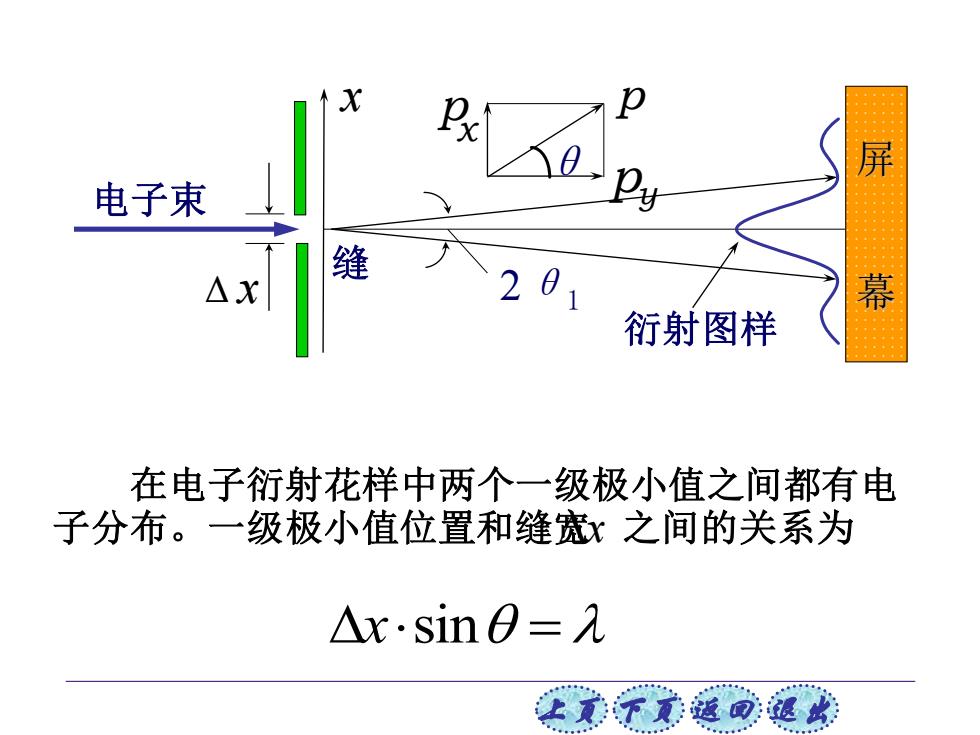
屏 电子束 缝 △X 26 幕 衍射图样 在电子衍射花样中两个一级极小值之间都有电 子分布。一级极小值位置和缝宽x之间的关系为 △x·sin0=λ 让美觉返司退
上页 下页 返回 退出 Δ x 2θ1 电子束 x 缝 屏 幕 衍射图样 p p p x θ y 在电子衍射花样中两个一级极小值之间都有电 子分布。一级极小值位置和缝宽 x 之间的关系为 = x sin

X方向电子的位置不确定量为△x 龙向的分动量△p的不确定量为△P AP:psin= h i h 2△x△x 所以△p·△x=h 考虑到在两个一级极小值之外还有电子出现, 所以有△p·△2h 经严格证明后应改写为: h 2 这就是海森伯坐标和动量的不确定关系式。 让美子意道可退此
上页 下页 返回 退出 所以 这就是海森伯坐标和动量的不确定关系式。 考虑到在两个一级极小值之外还有电子出现, 所以有 经严格证明后应改写为: P p P x θ y 方向的分动量 的不确定量为 x p x x p sin x h h p p x x = = = x 方向电子的位置不确定量为 x x = p x h p x x ≥ h x px ≥ 2 y py ≥ 2 z pz ≥ 2 ,

讨论: .不确定关系式说明用经典物理学量一一动量 、坐标来描写微观粒子行为时将会受到一定的限制 ,因为微观粒子不可能同时具有确定的动量及位置 坐标。 b.不确定关系式可以用来判别对于实物粒子其 行为究竟应该用经典力学来描写还是用量子力学来 描写。 c.对于微观粒子的能量E及它在能态上,停留的 平均时间△t之间也有下面的不确定关系: n △E△t≥ -2 让美下觉返司速此
上页 下页 返回 退出 讨论: a. 不确定关系式说明用经典物理学量——动量 、坐标来描写微观粒子行为时将会受到一定的限制 ,因为微观粒子不可能同时具有确定的动量及位置 坐标。 b. 不确定关系式可以用来判别对于实物粒子其 行为究竟应该用经典力学来描写还是用量子力学来 描写。 c. 对于微观粒子的能量E及它在能态上,停留的 平均时间 t 之间也有下面的不确定关系: E t ≥ 2

原子处于激发态的平均寿命一般为△t≈10-8s 于是激发态能级的宽度为 △E≥ ≈10-8s 2△t 这说明原子光谱有一定宽度,实验已经证实这一点。 上美不家返可退此
上页 下页 返回 退出 这说明原子光谱有一定宽度,实验已经证实这一点。 原子处于激发态的平均寿命一般为 8 t 10 s − 于是激发态能级的宽度为 E ≥ 8 10 s 2 t −