
§15-3原子核的放射性衰变 一、放射性衰变定律 1.原子核的衰变服从一定的统计规律: 设在tdt时间内有dN个原子核发生衰变, dN与当时存在的原子核数N成正比,与时间dt 成正比。 -dN=2Wdt(负号表示原子核数目在减小) N=Noe (N,为=0时刻原子核的数目) 放射性衰 变定律 让式不觉返司退
上页 下页 返回 退出 1. 原子核的衰变服从一定的统计规律: 设在t t+dt 时间内有dN个原子核发生衰变, dN与当时存在的原子核数N成正比,与时间dt 成正比。 → (N0为t=0时刻原子核的数目) 一、放射性衰变定律 0 t N N − = e 放射性衰 变定律 -d d N N t = (负号表示原子核数目在减小) §15-3 原子核的放射性衰变
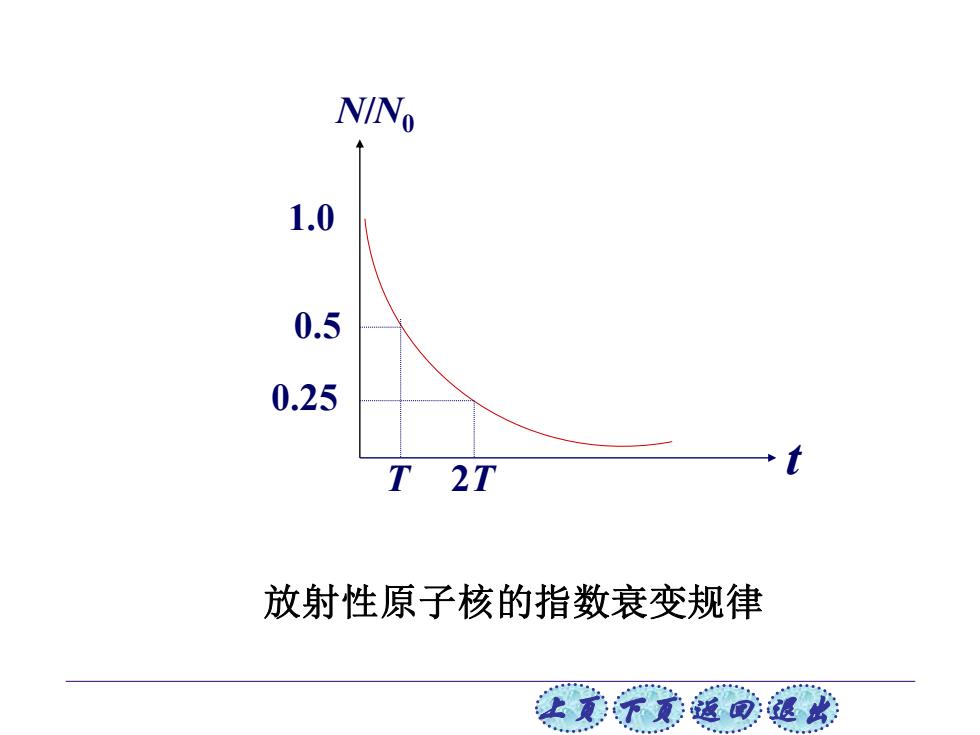
NINo 1.0 0.5 0.25 T 2T 放射性原子核的指数衰变规律 士美子文返回退此
上页 下页 返回 退出 N/N0 t 1.0 0.5 0.25 T 2T 放射性原子核的指数衰变规律

2.半衰期Ty2 衰变核数的一半所需时间 t=T,N= N 2 2 In 2 0.693 Te λ 决定于同位素自身的性质 让元不觉返司退此
上页 下页 返回 退出 0 1 2 2 N t T N = = , 衰变核数的一半所需时间 0 1 2 0 2 N T N − = e 1 2 ln 2 0.693 T = = 决定于同位素自身的性质 2. 半衰期 T1 2
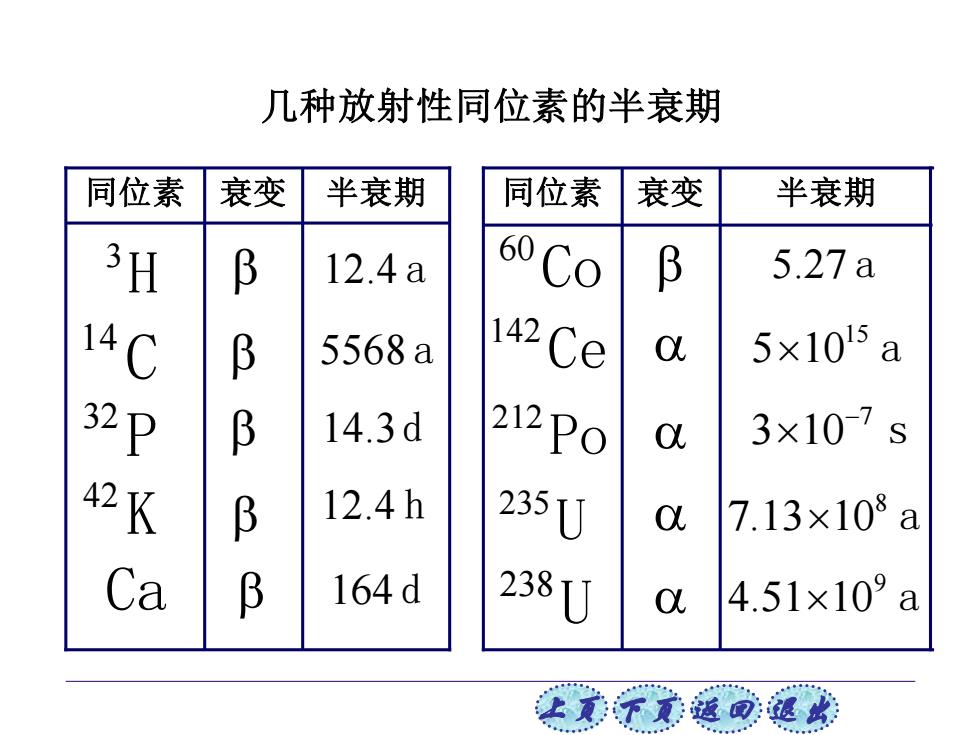
几种放射性同位素的半衰期 同位素 衰变 半衰期 同位素 衰变 半衰期 3H B 12.4a 60 Co B 5.27a 14C B 5568a 142Ce c 5×10l5a 32p B 14.3d 212P0 O以 3×10-7s K B 12.4h 235U a 7.13×108a Ca B 164d 238U 4.51×109a
上页 下页 返回 退出 几种放射性同位素的半衰期 同位素 衰变 半衰期 同位素 衰变 半衰期 42 K 32 P Ca 14.3d 12.4 h 164 d 3 H 12.4 a 14 C 5568 a 60 Co 142 Ce 212 Po 235 U 238 U 5.27 a 9 4.51 10 a 8 7.13 10 a 15 5 10 a 7 3 10 s −

平均寿命T 核在衰变前存在时间的平均值 在td时间内衰变了dN个核,每个核寿命为t -dw)∫aNd 1 可得 No No T2=1.4472 In 2 半衰期长,寿命长 让式不觉返司退
上页 下页 返回 退出 核在衰变前存在时间的平均值 平均寿命 在t→dt时间内衰变了dN个核,每个核寿命为t 0 0 0 0 0 0 ( ) 1 d d N N t N Nt t N N − = = = 可得 1 2 1 2 1.44 ln 2 T = = T 半衰期长,寿命长