石河子大学：《计量经济学》课程教学案例集（2013，共九个案例）

表2.5 2002年中国各地区城市居民人均年消费支出和可支配收入 地 区城市居民家庭平均每人每年消费支出（元）城市居民人均年可支配收入（元》 X 北京 10284.60 12463.92 天津 7191.96 9337.56 河北 5069.28 6679.68 山西 4710.96 5234.35 内蒙古 4859.88 6051.06 辽宁 5342.64 6524.52 吉林 4973.88 6260.16 黑龙江 4462.08 6100.56 上海 10464.04 13249.80 江苏 6042.60 8177.64 浙江 8713.08 11715.60 4736.52 6032.40 福建 6631.68 9189.36 江西 4549.32 6334.64 山东 5596.32 7614.36 问南 4504.68 6245.40 湖北 5608.92 6788.52 湖南 5574.72 6958.56 广东 8988.48 11137.20 广西 5413.44 7315.32 海南 5459.64 6822.72 重庆 6360.24 7238.04 四川 5413.08 6610.80 贵州 459828 5944.08 云南 5827.,92 7240.56 西藏 6952.44 8079.12 6

6 表 2.5 2002 年中国各地区城市居民人均年消费支出和可支配收入 地 区 城市居民家庭平均每人每年消费支出(元) Y 城市居民人均年可支配收入(元) X 北京 天津 河北 山西 内蒙古 辽宁 吉林 黑龙江 上海 江苏 浙江 安徽 福建 江西 山东 河南 湖北 湖南 广东 广西 海南 重庆 四川 贵州 云南 西藏 10284.60 7191.96 5069.28 4710.96 4859.88 5342.64 4973.88 4462.08 10464.00 6042.60 8713.08 4736.52 6631.68 4549.32 5596.32 4504.68 5608.92 5574.72 8988.48 5413.44 5459.64 6360.24 5413.08 4598.28 5827.92 6952.44 12463.92 9337.56 6679.68 5234.35 6051.06 6524.52 6260.16 6100.56 13249.80 8177.64 11715.60 6032.40 9189.36 6334.64 7614.36 6245.40 6788.52 6958.56 11137.20 7315.32 6822.72 7238.04 6610.80 5944.08 7240.56 8079.12

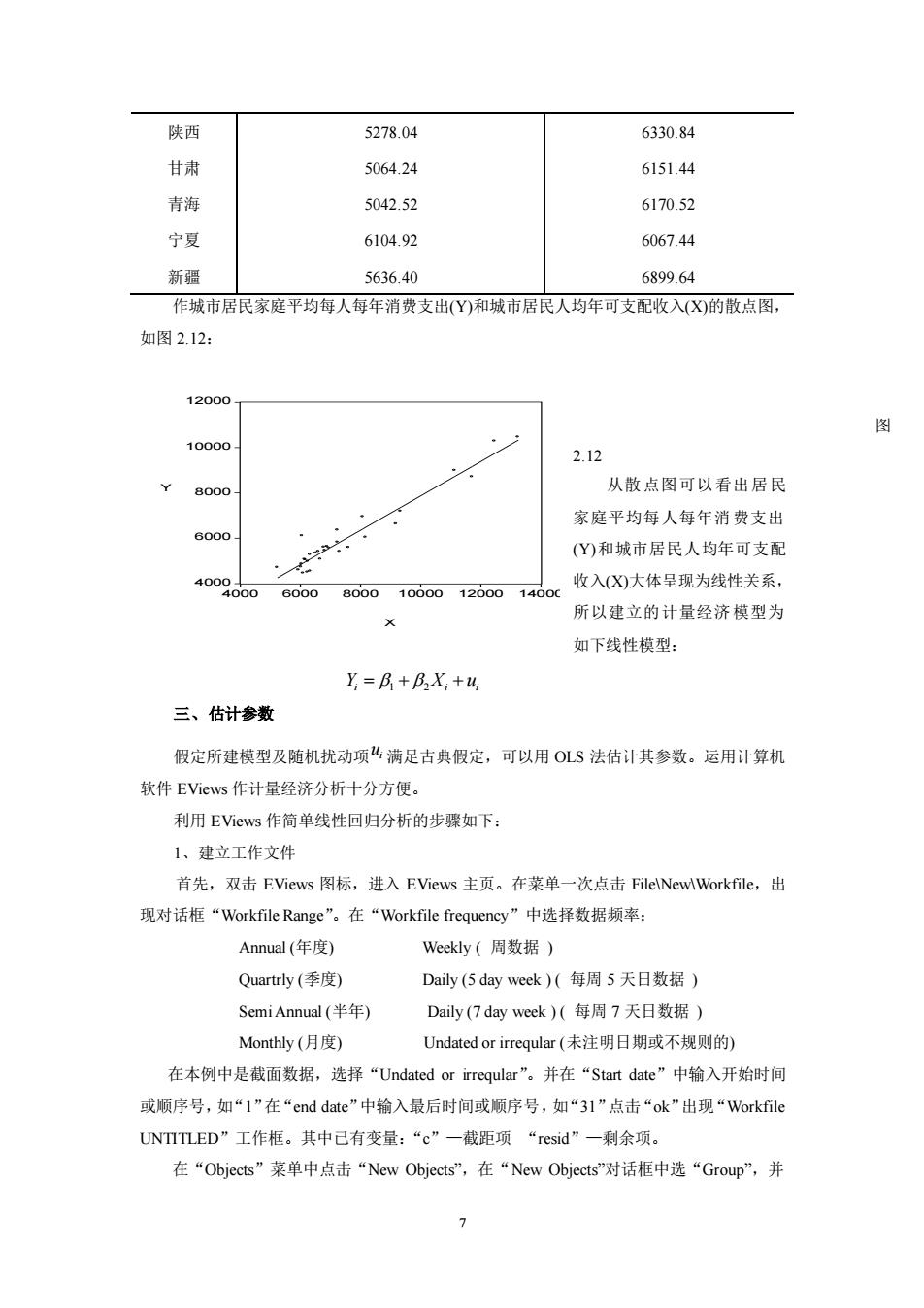
陕西 5278.04 6330.84 甘肃 5064.24 6151.44 青海 5042.52 6170.52 宁夏 6104.92 6067.44 新疆 5636.40 6899.64 作城市居民家庭平均每人每年消费支出(Y)和城市居民人均年可支配收入(X)的散点图， 如图2.12： 12000 10000 2.12 从散点图可以看出居民 家庭平均每人每年消费支出 (Y)和城市居民人均年可支配 80001000 2000 1400c 收入(X)大体呈现为线性关系， 所以建立的计量经济模型为 如下线性模型： y=月+月X+4 三、估计参数 假定所建模型及随机扰动项4满足古典假定，可以用OLS法估计其参数。运用计算机 软件EViews作计量经济分析十分方便。 利用EViews作简单线性回归分析的步骤如下： 1、建立工作文件 首先，双击EViews图标，进入EViews主页。在菜单一次点击FilelNewWorkfile,出 现对话框“Workfile Range”。在“Workfile frequeney”中选择数据须率： Annual(年度) WeckIy(周数据) Quartrly(季度) Daily(5 day week)(每周5天日数据) Semi Annual(半年) Daily(7 day week)(每周7天日数据) Monthly(月度) Undated or irreqular(未注明日期或不规则的) 在本例中是截面数据，选择“Undated or irreqular”。并在“Start date”中输入开始时间 或顺序号，如“1”在“end date”中输入最后时间或顺序号，如“31”点击“ok”出现“Workfile UNTITLED”工作框。其中已有变量：“c”一截距项“resid”一剩余项。 在“Objects”菜单中点击“New Objects”,在“New Objects'"对话框中选“Group”,并

7 陕西 甘肃 青海 宁夏 新疆 5278.04 5064.24 5042.52 6104.92 5636.40 6330.84 6151.44 6170.52 6067.44 6899.64 作城市居民家庭平均每人每年消费支出(Y)和城市居民人均年可支配收入(X)的散点图， 如图 2.12： 图 2.12 从散点图可以看出居民 家庭平均每人每年消费支出 (Y)和城市居民人均年可支配 收入(X)大体呈现为线性关系， 所以建立的计量经济模型为 如下线性模型： Y X u i i i = + +   1 2 三、估计参数 假定所建模型及随机扰动项 i u 满足古典假定，可以用 OLS 法估计其参数。运用计算机 软件 EViews 作计量经济分析十分方便。 利用 EViews 作简单线性回归分析的步骤如下： 1、建立工作文件 首先，双击 EViews 图标，进入 EViews 主页。在菜单一次点击 File\New\Workfile，出 现对话框“Workfile Range”。在“Workfile frequency”中选择数据频率： Annual (年度) Weekly ( 周数据 ) Quartrly (季度) Daily (5 day week ) ( 每周 5 天日数据 ) Semi Annual (半年) Daily (7 day week ) ( 每周 7 天日数据 ) Monthly (月度) Undated or irreqular (未注明日期或不规则的) 在本例中是截面数据，选择“Undated or irreqular”。并在“Start date”中输入开始时间 或顺序号，如“1”在“end date”中输入最后时间或顺序号，如“31”点击“ok”出现“Workfile UNTITLED”工作框。其中已有变量：“c”—截距项 “resid”—剩余项。 在“Objects”菜单中点击“New Objects”，在“New Objects”对话框中选“Group”，并 4000 6000 8000 10000 12000 4000 6000 8000 10000 12000 14000 X Y

在“Name for Objects'”上定义文件名，点击“OK”出现数据编辑窗口。 若要将工作文件存盘，点击窗口上方“Save”,在“SaveAs”对话框中给定路径和文件名， 再点击“k”,文件即被保存 2、输入数据 在数据编辑窗口中，首先按上行键“1”，这时对应的“os”字样的空格会自动上跳，在 对应列的第二个“os有边框的空格键入变量名，如“Y”,再按下行键“！”，对因变量名 下的列出现“NA”字样，即可依顺序输入响应的数据。其他变量的数据也可用类似方法输 入。 也可以在EViews命令框直接键入“data XY"气一元时)或“data Y,X,.”(多元 时)，回车出现“Group“"窗口数据编辑框，在对应的Y、X下输入数据。 若要对数据存盘，点击"fire/Save As'”,出现“Save As”"对话框，在“Drives”点所费 存的盘，在“Directories'”点存入的路径（文件名），在“Fire Name”对所存文件命名，或 点己存的文件名，再点“ok”。 若要读取己存盘数据，点击“fire/Open”,在对话框的Drives”点所存的磁盘名，在 Directories”点文件路径，在Fire Name”点文件名，点击“ok"即可。 3、估计参数 方法一：在EViews主页界面点击“Quick"菜单，点击“Estimate Equation”,出现“Equation specification”对话框，选OLS估计，即选击“Least Squares,健入“YCX”,点“ok”或 按回车，即出现如表2.6那样的回归结果。 表2.6 T2ged0bserw3itionsr31 Variable Coeficient Std.Error t-Statistic Prob. 23680963838 R-squared。 Mean dependent var 413159 Watson stat 11 Prob(F-statistic) n monoon 在本例中，参数估计的结果为： Y=282.2434+0.758511K (287.2649)(0.036928) =0.982520)(20.54026) 8

8 在“Name for Objects”上定义文件名，点击“OK”出现数据编辑窗口。 若要将工作文件存盘，点击窗口上方“Save”，在“SaveAs”对话框中给定路径和文件名， 再点击“ok”，文件即被保存。 2、输入数据 在数据编辑窗口中，首先按上行键“↑”，这时对应的“obs”字样的空格会自动上跳，在 对应列的第二个“obs”有边框的空格键入变量名，如“Y”，再按下行键“↓”，对因变量名 下的列出现“NA”字样，即可依顺序输入响应的数据。其他变量的数据也可用类似方法输 入。 也可以在 EViews 命令框直接键入“data X Y ”(一元时) 或 “data Y X1 X2 . ”(多元 时)，回车出现“Group”窗口数据编辑框，在对应的 Y、X 下输入数据。 若要对数据存盘，点击 “fire/Save As”，出现“Save As”对话框，在“Drives”点所要 存的盘，在“Directories”点存入的路径（文件名），在“Fire Name”对所存文件命名，或 点已存的文件名，再点“ok”。 若要读取已存盘数据，点击“fire/Open”，在对话框的“Drives”点所存的磁盘名，在 “Directories”点文件路径，在“Fire Name”点文件名，点击“ok”即可。 3、估计参数 方法一：在 EViews 主页界面点击“Quick”菜单，点击“Estimate Equation”，出现“Equation specification”对话框，选 OLS 估计，即选击“Least Squares”，键入“Y C X”，点“ok”或 按回车，即出现如表 2.6 那样的回归结果。 表 2.6 在本例中，参数估计的结果为： ^ Y X i i = + 282.2434 0.758511 （287.2649） (0.036928) t=(0.982520) (20.54026)

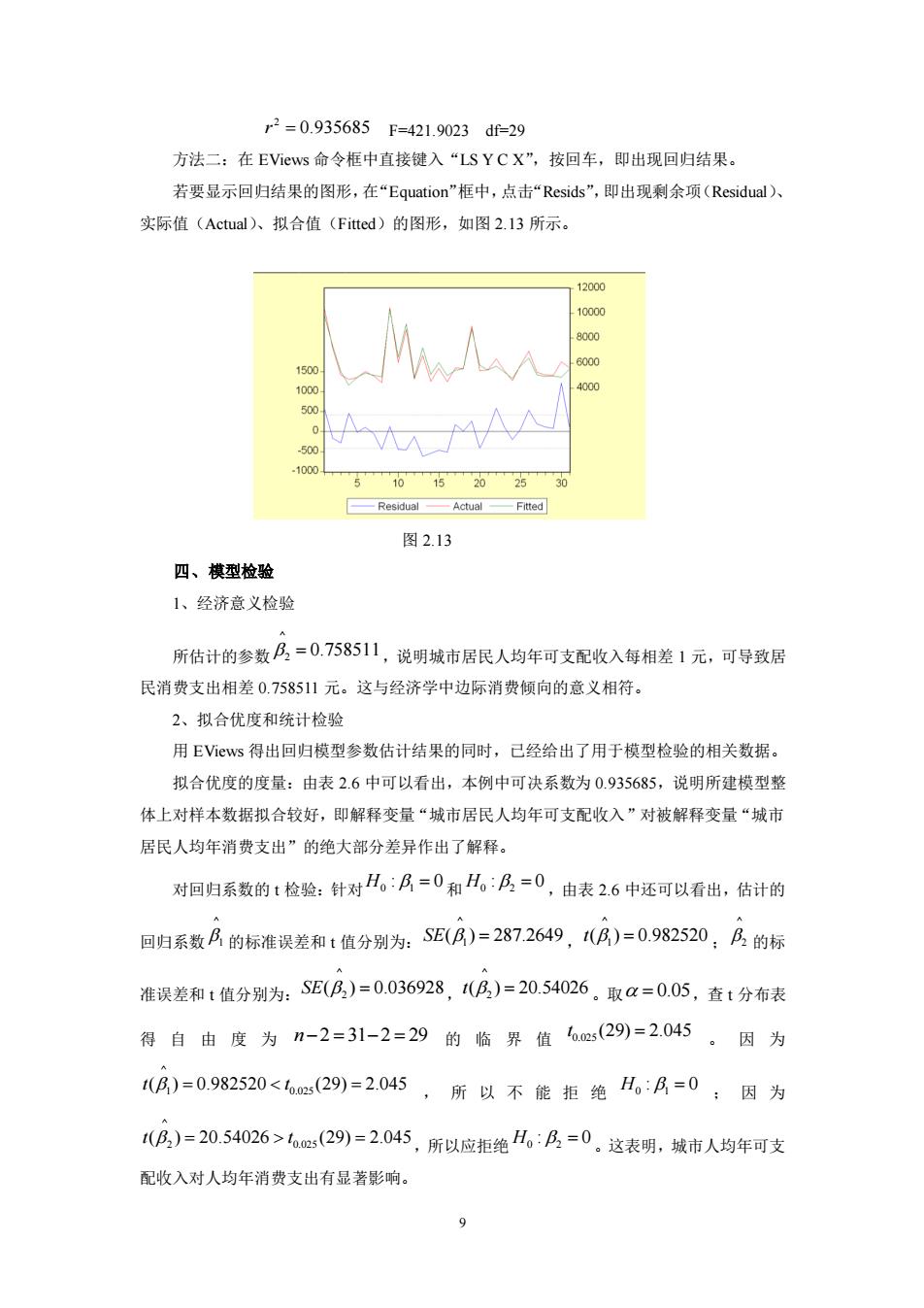
2=0.935685F=421.9023d=29 方法二：在EViews命令框中直接键入“LSYCX”,按回车，即出现回归结果。 若要显示回归结果的图形，在“Equation'”框中，点击“Resids”,即出现剩余项(Residual), 实际值(Actual、拟合值(Fitted)的图形，如图2.13所示。 2000 1000 5 500 505为53 -Residual 图2.13 四、模型检验 1、经济意义检验 所估计的参数B,=0.758511,说明城市居民人均年可支配收入每相差1元，可导致居 民消费支出相差0.758511元。这与经济学中边际消费倾向的意义相符。 2、拟合优度和统计检验 用EVws得出回归模型参数估计结果的同时，己经给出了用于模型检验的相关数据。 拟合优度的度量：由表2.6中可以看出，本例中可决系数为0.935685，说明所建模型整 体上对样本数据拟合较好，即解释变量“城市居民人均年可支配收入”对被解释变量“城市 居民人均年消费支出”的绝大部分差异作出了解释。 对回归系数的1检验：针对H,:月=0和H,B=0,由表26中还可以看出，估计的 回归系数月的标准误差和t值分别为：SE(月)=287.2649,1(B)=0.982520,B的标 准误差和1值分别为：SE(B,)=0.036928,1(月，)=20.54026.取a=0.05,查t分布表 得自由度为n-2=31-2=29的临界值6m(29)=2.045。因为 ()=0.982520<s(29)=2045，所以不能拒绝:月=0因为 1B,)=20.54026>6(29)=2.045,所以应拒绝H。:B=0。这表明，城市人均年可支 配收入对人均年消费支出有显著影响

9 2 r = 0.935685 F=421.9023 df=29 方法二：在 EViews 命令框中直接键入“LS Y C X”，按回车，即出现回归结果。 若要显示回归结果的图形，在“Equation”框中，点击“Resids”，即出现剩余项（Residual）、 实际值（Actual）、拟合值（Fitted）的图形，如图 2.13 所示。 图 2.13 四、模型检验 1、经济意义检验 所估计的参数 ^ 2 = 0.758511 ，说明城市居民人均年可支配收入每相差 1 元，可导致居 民消费支出相差 0.758511 元。这与经济学中边际消费倾向的意义相符。 2、拟合优度和统计检验 用 EViews 得出回归模型参数估计结果的同时，已经给出了用于模型检验的相关数据。 拟合优度的度量：由表 2.6 中可以看出，本例中可决系数为 0.935685，说明所建模型整 体上对样本数据拟合较好，即解释变量“城市居民人均年可支配收入”对被解释变量“城市 居民人均年消费支出”的绝大部分差异作出了解释。 对回归系数的 t 检验：针对 0 1 H : 0  = 和 0 2 H : 0  = ，由表 2.6 中还可以看出，估计的 回归系数 ^ 1 的标准误差和 t 值分别为： ^ 1 SE( ) 287.2649  = ， ^ 1 t( ) 0.982520  = ； ^ 2 的标 准误差和 t 值分别为： ^ 2 SE( ) 0.036928  = ， ^ 2 t( ) 20.54026  = 。取  = 0.05 ，查 t 分布表 得自由度为 n− = − = 2 31 2 29 的临界值 0.025 t (29) 2.045 = 。因为 ^ 1 0.025 t t ( ) 0.982520 (29) 2.045  =  = ，所以不能拒绝 0 1 H : 0  = ；因为 ^ 2 0.025 t t ( ) 20.54026 (29) 2.045  =  = ，所以应拒绝 0 2 H : 0  = 。这表明，城市人均年可支 配收入对人均年消费支出有显著影响

五、回归预测 由表2.5中可看出，2002年中国西部地区城市居民人均年可支配收入除了西藏外均在 8000以下，人均消费支出也都在7000元以下。在西部大开发的推动下，如果西部地区的城 市居民人均年可支配收入第一步争取达到1000美元（按现有汇率即人民币820元），第二步 再争取达到1500美元（即人民币12405元），利用所估计的模型可预测这时城市居民可能达 到的人均年消费支出水平。可以注意到，这里的预测是利用截面数据模型对被解释变量在不 同空间状况的空间预测。 用EViews作回归预测，首先在“Workfile”窗口点击“Range"”,出现“Change Workfile Range”窗口，将“End data"由“31”改为“33”，点“OK”,将“Workfile”中的“Range” 扩展为1一33。在“Workfile”窗口点击“sampl'”,将“sampl"窗口中的“131”改为“133” 点“OK”,将样本区也改为1一33。 为了输入Xn=8270,Xn=12405在EViews命令框睫入data回车，在X数据表 中的“32”位置输入“8270”，在“33”的位置输入“12405”，将数据表最小化。 然后在“quation”框中，点击“Forecast”,得对话框。在对话框中的“Forecast nane' (预测值序列名)键入。Y”,回车即得到模型估计值及标准误差的图形。双击“woke 窗口中出现的~少”在“少”数据表中的“32”位置出现预测值'=655.132，在“33 位置出现'n=9691.577.这是当Xn=8270和Xn=12405时人均消费支出的点预测 值。 为了作区间预测，在X和Y的数据表中，点击“Vicw选“Descriptive Stats\Cmmon Sample“,则得到X和Y的描述统计结果，见表2.7： 表2.7 lean 7515.0265982.476 Median 6788.5205459.640 ximum Skewness 1585893 1629968 Kurtosis 4.4586454.787999 17517 0.000820.000133 根据表2.7的数据可计算 Observations 31 31 ∑x=62n-1)=2042.6822×(31-1)=125176492.59 (X1-X)2=(8270-7515.0262=569985.74 10

10 五、回归预测 由表 2.5 中可看出，2002 年中国西部地区城市居民人均年可支配收入除了西藏外均在 8000 以下，人均消费支出也都在 7000 元以下。在西部大开发的推动下，如果西部地区的城 市居民人均年可支配收入第一步争取达到 1000 美元(按现有汇率即人民币 8270 元)，第二步 再争取达到 1500 美元(即人民币 12405 元)，利用所估计的模型可预测这时城市居民可能达 到的人均年消费支出水平。可以注意到，这里的预测是利用截面数据模型对被解释变量在不 同空间状况的空间预测。 用 EViews 作回归预测，首先在“Workfile”窗口点击“Range”，出现“Change Workfile Range”窗口，将“End data”由“31”改为“33”，点“OK”，将“Workfile”中的“Range” 扩展为 1—33。在“Workfile”窗口点击“sampl”，将“sampl”窗口中的“1 31”改为“1 33”， 点“OK”，将样本区也改为 1—33。 为了输入 X f 1 = 8270 ， X f 2 =12405 在 EViews 命令框键入 data x /回车, 在 X 数据表 中的“32”位置输入“8270”，在“33”的位置输入“12405”，将数据表最小化。 然后在“E quation ”框中，点击“Forecast”，得对话框。在对话框中的“Forecast name” (预测值序列名)键入“ Yf ”， 回车即得到模型估计值及标准误差的图形。双击“Workfile” 窗口中出现的“ Yf ”，在“ Yf ”数据表中的“32”位置出现预测值 Yf 1 = 6555.132 ，在“33” 位置出现 Yf 2 = 9691.577 。这是当 X f 1 = 8270 和 X f 2 =12405 时人均消费支出的点预测 值。 为了作区间预测，在 X 和 Y 的数据表中，点击“View”选“Descriptive Stats\Cmmon Sample”，则得到 X 和 Y 的描述统计结果，见表 2.7: 表 2.7 根据表 2.7 的数据可计算: 2 2 2 x n i x = − =  − =  ( 1) 2042.682 (31 1) 125176492.59 2 2 1 ( ) (8270 7515.026) 569985.74 X X f − = − =