秦 也就是说,Hx是x关于超平面span{v}的镜面反射 因此,Householder矩阵有时也称为Householder反射或反射矩阵 span(v) Hx Householder变换的几何意义 http://math.ecnu.edu.cn/~jypan 11/54
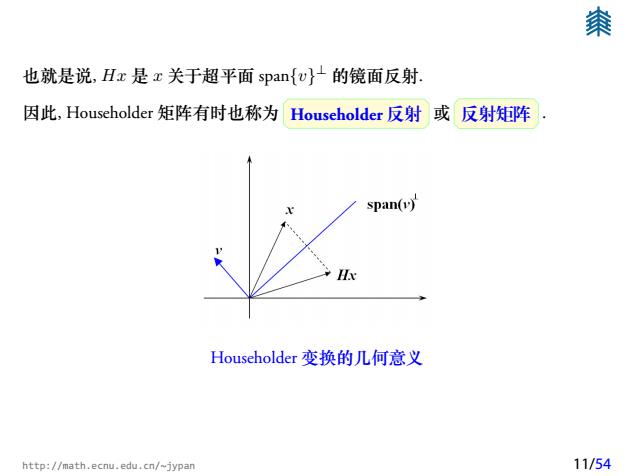
也就是说, Hx 是 x 关于超平面 span{v} ⊥ 的镜面反射. 因此, Householder 矩阵有时也称为 Householder 反射 或 反射矩阵 . Householder 变换的几何意义 http://math.ecnu.edu.cn/~jypan 11/54

秦 Householder矩阵的几个基本性质 定理设H∈Cnxn是一个Householder矩阵,则 (I)H*=H,即H Hermite的; (2)H*H=I,即H是酉矩阵; (3)H2=I,所以H-1=H; (4)det(H)=-1; (⑤)H有两个互异的特征值:入=1和入=-1,其中入=1的代数重数为 n-1. http://math.ecnu.edu.cn/~jypan 12/54
Householder 矩阵的几个基本性质 定理 设 H ∈ C n×n 是一个 Householder 矩阵, 则 (1) H∗ = H, 即 H Hermite 的; (2) H∗H = I, 即 H 是酉矩阵; (3) H2 = I, 所以 H−1 = H ; (4) det(H) = −1; (5) H 有两个互异的特征值: λ = 1 和 λ = −1, 其中 λ = 1 的代数重数为 n − 1. http://math.ecnu.edu.cn/~jypan 12/54

秦 Householder矩阵的重要应用 Householder变换可以将一个向量除第一个元素以外的所有元素都化为零 先给出一个一般性结论 引理设x,y∈Cn为任意两个互异的向量,则存在一个Householder矩阵 H(v)使得y=H(o)x的充要条件是x2=ly2且x*y∈R. (取v=x-y即可) (板书) 若x,y都是实向量,则x*y∈R自然成立,此时充要条件为 llxll2=llyll2 http://math.ecnu.edu.cn/~jypan 13/54
Householder 矩阵的重要应用 Householder 变换可以将一个向量除第一个元素以外的所有元素都化为零 先给出一个一般性结论 引理 设 x, y ∈ C n 为任意两个互异的向量, 则存在一个 Householder 矩阵 H(v) 使得 y = H(v)x 的充要条件是 ∥x∥2 = ∥y∥2 且 x ∗y ∈ R. (取 v = x − y 即可) (板书) ✍ 若x, y 都是实向量, 则 x ∗y ∈ R 自然成立, 此时充要条件为 ∥x∥2 = ∥y∥2 http://math.ecnu.edu.cn/~jypan 13/54

秦 定理设x=[r1,r2,,xnJT∈Rn非零,则存在Householder矩阵H(u)使得 H(v)x=ae1,其中a=x2(或a=-‖x2,e1=[1,0,,0jT∈Rn. 在后面的讨论中,我们把定理中的向量v称为x对应的 Householder向量 http://math.ecnu.edu.cn/~jypan 14/54
定理 设 x = [x1, x2, . . . , xn] ⊺ ∈ R n 非零, 则存在 Householder 矩阵 H(v) 使得 H(v)x = αe1, 其中 α = ∥x∥2 (或 α = −∥x∥2), e1 = [1, 0, . . . , 0]⊺ ∈ R n . ✍ 在后面的讨论中,我们把定理中的向量 v 称为 x 对应的 Householder 向量 http://math.ecnu.edu.cn/~jypan 14/54

秦 Householder向量的i计算 设x=【x1,x2,·,cn]T∈R”,由引理证明过程可知,对应的Householder向量为 v=x-ae1=[1-a,Z2;.....Un]. 在实际计算中,为尽可能地减少舍入误差,应避免两个相近的数湘减,因此取 a=-sign(x1)·lxll2 事实上,我们也可以取a=sig(x1)川x2,但此时为了减少舍入误差,我 们需要通过下面的公式来计算v的第一个分量1 1=x1-a= -川喔。=-(吃+吃+…+) z1+a z1+a http://math.ecnu.edu.cn/~jypan 15/54
Householder 向量的计算 设 x = [x1, x2, . . . , xn] ⊺ ∈ R n , 由引理证明过程可知, 对应的 Householder 向量为 v = x − αe1 = [x1 − α, x2, . . . , xn] ⊺ . 在实际计算中, 为尽可能地减少舍入误差, 应避免两个相近的数湘减, 因此取 α = − sign(x1) · ∥x∥2 ✍ 事实上, 我们也可以取 α = sign(x1)∥x∥2, 但此时为了减少舍入误差, 我 们需要通过下面的公式来计算 v 的第一个分量 v1 v1 = x1 − α = x 2 1 − ∥x∥ 2 2 x1 + α = −(x 2 2 + x 2 3 + · · · + x 2 n ) x1 + α . http://math.ecnu.edu.cn/~jypan 15/54