
第24卷第2期 振动工程学报 Vol.24 No.2 2011年4月 Journal of Vibration Engineering Apr.2011 随机结构动力特征的统计矩及灵敏度分析研究 宋述芳,吕震宙,乔红威 (西北工业大学航空学院,陕西西安710072) 摘要:结构参数的不确定性会导致结构的动力特征(如自振顿率、振型等)等具有不确定性,如果采用确定性分析方 法进行结构设计可能会使结构处于比较危险的状态,因此对随机结构的动力特性分析是十分有必要的。由于统计 矩反映了随机结构动力特征的统计特性,由这些统计矩就可以进一步掌握可靠性分析所需要的动力特征的分布规 律。统计矩的灵敏度分析能够判别结构不确定性参数对结构动力特征的重要程度,从而为改进结构设计模型提供 有效途径。建立了基于MCMC的分层抽样法,并采用该方法对结构动力特性进行统计矩的估计,并通过统计随机 样本点信息进行统计矩的灵敏度分析,通过算例验证了所提方法的优越性。 关镀词:随机结构;统计矩:灵敏度分析;动力特征:基于MCMC的分层抽样法 中图分类号:TB114.3:TU311.3文献标识码:A文童编号:1004-4523(2011)02-0133-06 梁、杆、板等简单结构,可以很方便地与有限元分析 引言 软件(如MSC.Nastran,Ansys等)相结合进行大型 结构的随机结构动力特征的分析。 在结构动力学分析中,主要包括结构动力响应 和结构动力特征分析两方面内容。所谓的结构动力 1随机结构的动力特征及其灵敏度分析 特性包括结构的固有频率、振型、刚度以及质量分布 等诸多内容,这是人们在动力学内涉及最早也是成 结构动力特性主要包括结构的固有领率和振 果较为丰富的领域1~】。动力特征分析通常用于验 型,这里仅考虑结构的固有频率。对于一个具有n自 证结构的固有频率是否远离激励频率,或者通过修 由度的无阻尼自由振动结构,其运动微分方程用矩 改动力特征值来诚少或抑制结构振动。传统的确定 阵形式可表示为] 性结构动力特征分析已趋于成熟,随着概率设计方 M Ky=0 (1) 法在工程实际中的普遍应用,考虑参数随机性的结 式中M,R,y和夕分别为结构质量矩阵、刚度矩 构动力特征分析亦引起了不少学者的关注,如今已 阵、位移列阵和加速度列阵。 成为动力学领域内的一个重要专题一副。 从式(1)的运动微分方程求解结构的固有频率, 结构参数的不确定性会导致结构动力特征具有 由结构的边界条件可以推知结构的特征矩阵为K一 不确定性,由于随机结构动力特性的统计矩包含了 w2M,而|K一M|=0被称为频率方程或特征方 它的统计特性,利用动力特性的统计矩可以得到其 程,从中得出n个正实根,并按从小到大排列,:≤ 概率分布,进而得到可靠性分析所需要的统计信息。 +:(i=1,2,…,n),代人方程[K-w2M]y=0,得到 统计矩的灵敏度分析能够判别不确定性参数对动力 系统的主振型或固有振型1)。 特性的重要程度,为改进结构设计模型提供有效途 而在随机结构分析中,质量矩阵和刚度矩阵是 径3)。确定性结构的动力特征值灵敏度分析成果很 随机变量向量x的函数,x代表结构的尺寸、物理参 丰富,相比之下,只有很少关于随机结构动力特征灵 数等具有随机性的变量,可以将随机结构的动力特 敏度分析的文献。本文采用基于MCMC的分层抽样 征分析转换成传统的随机分析问题,结构的第;个 法进行结构动力特性的统计矩估计,并通过统计随 特征值固有频率函数山(x)就变成了x的隐函数,它 机样本点信息进行统计矩的灵敏度分析,分析方法 的统计特征为 的基本实现步骤具有较强的适用范围,并不局限于 收稿日期:2010-07-13:修订日期:2011-01-10 基金项目:国家自然科学基金(NSFC50875213)和西北工业大学基础研究基金(NPU-FFR-JC20100201)资助项目 万方数据
第24卷第2期 2011年4月 振 动 工 程 学 报 Journal of Vibration Engineering VoI.24 No.2 Apr.2011 随机结构动力特征的统计矩及灵敏度分析研究 宋述芳,吕震宙,乔红威 (西北工业大学航空学院,陕西西安710072) 摘要:结构参数的不确定性会导致结构的动力特征(如自振频率、振型等)等具有不确定性.如果采用确定性分析方 法进行结构设计可能会使结构处于比较危险的状态.因此对随机结构的动力特性分析是十分有必要的。由于统计 矩反映了随机结构动力特征的统计特性.由这些统计矩就可以进一步掌握可靠性分析所需要的动力特征的分布规 律。统计矩的灵敏度分析能够判别结构不确定性参数对结构动力特征的重要程度,从而为改进结构设计模型提供 有效途径。建立了基于MCMC的分层抽样法。并采用该方法对结构动力特性进行统计矩的估计,并通过统计随机 样本点信息进行统计矩的灵敏度分析.通过算例验证了所提方法的优越性。 关键词:随机结构;统计矩;灵敏度分析l动力特征;基于MCMC的分层抽样法 中图分类号:TBll4.3;TU311.3 文献标识码:A 文章编号:l004—4523(2011)02一0133一06 引 言 在结构动力学分析中,主要包括结构动力响应 和结构动力特征分析两方面内容。所谓的结构动力 特性包括结构的固有频率、振型、刚度以及质量分布 等诸多内容,这是人们在动力学内涉及最早也是成 果较为丰富的领域【l~3】。动力特征分析通常用于验 证结构的固有频率是否远离激励频率,或者通过修 改动力特征值来减少或抑制结构振动。传统的确定 性结构动力特征分析已趋于成熟,随着概率设计方 法在工程实际中的普遍应用,考虑参数随机性的结 构动力特征分析亦引起了不少学者的关注,如今已 成为动力学领域内的一个重要专题[4q]。 结构参数的不确定性会导致结构动力特征具有 不确定性,由于随机结构动力特性的统计矩包含了 它的统计特性,利用动力特性的统计矩可以得到其 概率分布,进而得到可靠性分析所需要的统计信息。 统计矩的灵敏度分析能够判别不确定性参数对动力 特性的重要程度,为改进结构设计模型提供有效途 径【8’9]。确定性结构的动力特征值灵敏度分析成果很 丰富,相比之下,只有很少关于随机结构动力特征灵 敏度分析的文献。本文采用基于MCMC的分层抽样 法进行结构动力特性的统计矩估计,并通过统计随 机样本点信息进行统计矩的灵敏度分析,分析方法 的基本实现步骤具有较强的适用范围,并不局限于 梁、杆、板等简单结构,可以很方便地与有限元分析 软件(如MSC.Nastran、Ansys等)相结合进行大型 结构的随机结构动力特征的分析。 1 随机结构的动力特征及其灵敏度分析 结构动力特性主要包括结构的固有频率和振 型,这里仅考虑结构的固有频率。对于一个具有靠自 由度的无阻尼自由振动结构,其运动微分方程用矩 阵形式可表示为[83 肘夕+的一0 (1) 式中 肘,x,j,和夕分别为结构质量矩阵、刚度矩 阵、位移列阵和加速度列阵。 从式(1)的运动微分方程求解结构的固有频率, 由结构的边界条件可以推知结构的特征矩阵为必一 cc,z肘,而I K一∞2肘l=O被称为频率方程或特征方 程,从中得出以个正实根,并按从小到大排列,峨≤ 皑+l(i=1,2,…,n),代人方程[K一∞2竹]J,=o,得到 系统的主振型或固有振型[1引。 而在随机结构分析中,质量矩阵和刚度矩阵是 随机变量向量工的函数,工代表结构的尺寸、物理参 数等具有随机性的变量,可以将随机结构的动力特 征分析转换成传统的随机分析问题,结构的第i个 特征值固有频率函数咄(工)就变成了工的隐函数,它 的统计特征为 收稿日期:2010—07—13;修订日期:2011一01—10 基金项目:国家自然科学基金(NSFC50875213)和西北工业大学基础研究基金(NPU—FFR—JC20100201)资助项目 万方数据

134 振动工程学报 第24卷 =0(x)x(x)dx (2) fwr.os (4) -(-/:()d] 正=gx)-,fxr)dr= 式中∫x(x)为基本变量x={x1,x2,…,x}的联合 概率密度函数,R为n维变量空间,4和o分别为 2,g国-4fr= 仙(x)的均值和标准差。而计算随机结构动力特性的 各阶统计矩在数学上就是计算式(2)的积分。 FnP(- 定义,(x)的统计矩灵敏度为4,和a对基本变 2P.s国-wiau (5) 量分布参数日,(包括随机变量的均值、方差等)的偏 导数,它能够反映基本变量对统计矩的影响。 飞F. 瓷-=[] 飞F L 8)-b. La0.丁x(x)J )b fx(x) 2E[u,(x)-4)]冠} g(r)b (3) 显然仙,(x)的统计矩及灵敏度信息都可以通过 F Monte Carlo模拟进行求解,但所需要的计算量太 大,对于大型复杂结构来说其计算量不可接受。可靠 图1 基于MCMC的分层抽样引人中间事件的示意图 性研究人员提出了一系列方差缩威技术)],如重要 抽样、分层抽样、子集模拟法、线抽样等,其中子集模 分别对式(4)和(5)两端关于随机变量分布参数 拟法具有Monte Carlo模拟的优点,对变量的维数、 的导数,得到基于MCMC的分层抽样法的统计矩灵 分布形式,功能函数的形式等没有任何限制,但其计 敏度的计算公式为 算效率比Monte Carlo模拟要高很多。本文在子集 模拟法的基础上1-,建立了基于马尔可夫Monte 0-2P[e]r+ 8。 Carlo(MCMC)的分层抽样法,它的基本思想是将整 aP(F) Jr[g(x)fx(xIF.)]dx (6) 个变量空间划分为一系列互不相容的子空间,通过 对子空间进行样本点的模拟和统计,实现结构响应 意=六2.a-wiau+ 的统计矩和灵敏度分析。 P(F(-)F2]dx- 2基于MCMC的分层抽样法 2P(F) 0【g)-4 fx*IF]ar 基于MCMC的分层抽样法将整个变量空间划 (7) 分为一系列互不相容的子空间,如图1所示。通过引 通过统计条件样本的信息,即可得到统计矩灵敏度 人一系列的临界值b1,b2,·,b将概率空间划分为 的估计值。 互不相容的空间F,(k=0,1,…,m),此时有F。U 式(4)和(5)中的条件概率P(F,)的估计值需要 FUUF.=R",且F,∩F,=中。以下为了叙述方 通过抽取条件样本点进行估计。尽管服从条件分布 便,设所研究问题g(x)中包含的基本随机向量x= 的样本点可以直接由Monte Carlo法抽取,但是这 {x1x2,·,x.},x的联合概率密度函数为fx(x),依 种抽样方法的效率很低,本文采用MCMC来高效地 据统计矩的定义及事件的互不相容性,可得到如下 模拟条件样本点,进而估计概率P(F,)和统计矩。此 所示的功能响应的矩估计计算公式 外,中间事件的选择在统计矩估计的过程中起着重 -s,(s-gc)/(r- 要作用。对于中间事件的选择,需要在模拟条件样本 点数和中间失效事件的个数m上采取折衷的方法, PF.J.[(gfx/P(F]os- 本文通过设定概率P。并进行自动分层的方法来实 现临界值b,(i=1,2,·,m)的取值和统计矩及灵敏 万方数据
134 振 动 工 程 学 报 第24卷 I^2 II_皑(工)厂x(工)如 -{ :: 1寻 (2) 【q 2 LJt.(哪(工)一^)2^(工)以j 2 式中 ^(工)为基本变量工={z,,z:,…,z。)的联合 概率密度函数,Ⅳ为,z维变量空间,雎.和乳。分别为 毗(x)的均值和标准差。而计算随机结构动力特性的 各阶统计矩在数学上就是计算式(2)的积分。 定义咄(工)的统计矩灵敏度为雎i和几.对基本变 量分布参数以(包括随机变量的均值、方差等)的偏 导数,它能够反映基本变量对统计矩的影响。 瓮=『1.掣吣m=E[掣怒] 象=壶{E[掣掣卜 2球吣)一^)]甏} (3) 显然咄(J)的统计矩及灵敏度信息都可以通过 Monte Carlo模拟进行求解,但所需要的计算量太 大,对于大型复杂结构来说其计算量不可接受。可靠 性研究人员提出了一系列方差缩减技术[9],如重要 抽样、分层抽样、子集模拟法、线抽样等,其中子集模 拟法具有Monte CarIo模拟的优点,对变量的维数、 分布形式,功能函数的形式等没有任何限制,但其计 算效率比Monte Carlo模拟要高很多。本文在子集 模拟法的基础上[11叫¨,建立了基于马尔可夫Monte Carlo(MCMC)的分层抽样法,它的基本思想是将整 个变量空间划分为一系列互不相容的子空间,通过 对子空同进行样本点的模拟和统计,实现结构响应 的统计矩和灵敏度分析。 2 基于MCMC的分层抽样法 基于MCMC的分层抽样法将整个变量空间划 分为一系列互不相容的子空间,如图l所示。通过引 入一系列的临界值6,,6:,…,6_将概率空间划分为 互不相容的空间R(七=O,1,…,优),此时有F。U F,U…UF。一Ⅳ,且Fjn凡=声。以下为了叙述方 便,设所研究问题g(工)中包含的基本随机向量工= {z。,z:,…,毛},工的联合概率密度函数为^(工),依 据统计矩的定义及事件的互不相容性,可得到如下 所示的功能响应的矩估计计算公式 广』生r 心5 J矿譬(工)厶(工)如。荟J矿[to)g(.r)^(工)]妇= ∑尸(F.)I』t(j)g(工)^(工)/P(凡)p= ∑P(n)l』g(工)^(z限)批 (4) ●-O J^ 《2 J∥(g(工)一心)2^(工)以2 善J矿_(以础)_∥^(州工一 ∑P(n)I,[f‘(r)(g(z)一心)2厶o)/P(n)]如= l=O o^ 妻眦·),F[(咖)一∥^(郴洲如 (5) ~. j龟z 够,蚍舒 、也删= 、, k莲 D 山g(磅=6, 疑谶:∞=以 6l 图1基于MCMC的分层抽样引入中间事件的示意图 分别对式(4)和(5)两端关于随机变量分布参数 的导数,得到基于MCMC的分层抽样法的统计矩灵 敏度的计算公式为 甏=毒眦,肌∽掣卜+ 掣肛(工胤郴加出 (6) 爰=壶耋{掣心础卜旷舶脚计 P(R).『。。[(g(工)一心)2半]dz一 2P(¨擎Jl_№(工)一心)^(工限)弘) (7) 通过统计条件样本的信息,即可得到统计矩灵敏度 的估计值。 式(4)和(5)中的条件概率P(凡)的估计值需要 通过抽取条件样本点进行估计。尽管服从条件分布 的样本点可以直接由Monte carlo法抽取,但是这 种抽样方法的效率很低,本文采用MCMC来高效地 模拟条件样本点,进而估计概率P(凡)和统计矩。此 外,中间事件的选择在统计矩估计的过程中起着重 要作用。对于中间事件的选择,需要在模拟条件样本 点数和中间失效事件的个数优上采取折衷的方法, 本文通过设定概率户。并进行自动分层的方法来实 现临界值抚(i=1,2,…,优)的取值和统计矩及灵敏 万方数据

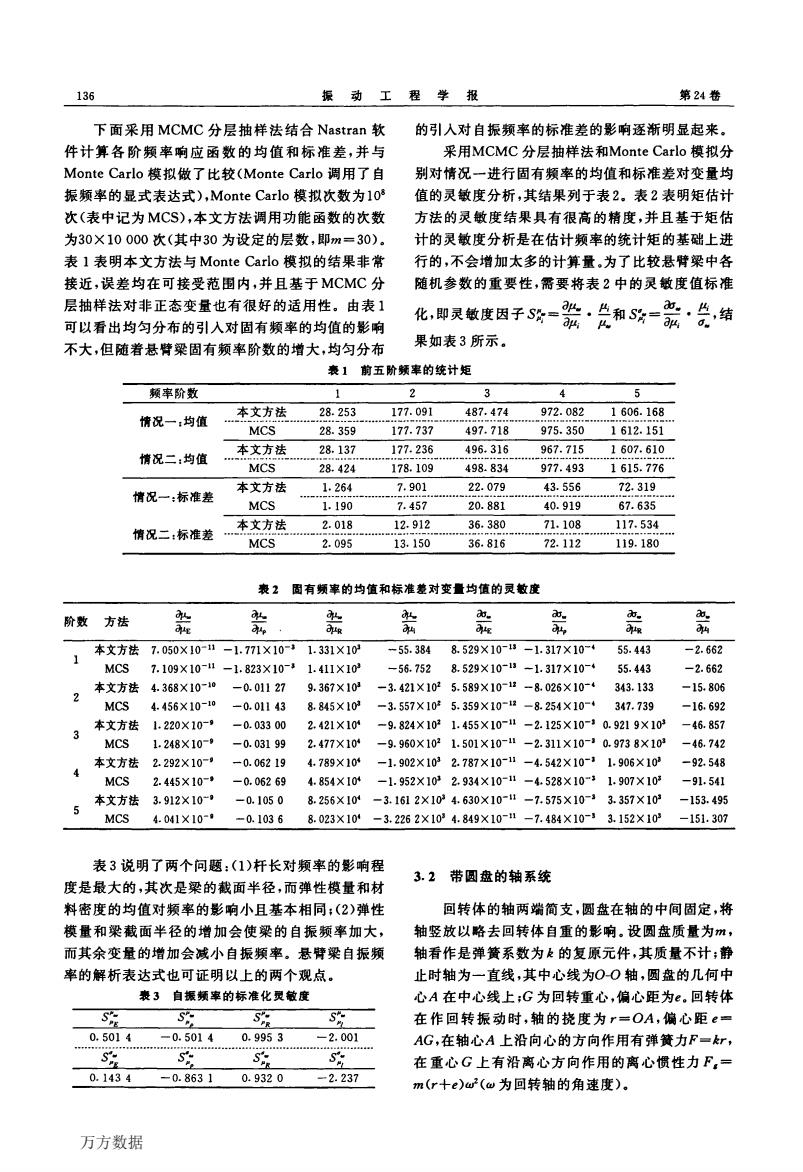
第2期 宋述芳,等:随机结构动力特征的统计矩及灵敏度分析研究 135 度分析,其具体的实现流程图参见图2。 析的形式,下面列出前五阶固有频率的解析表达式 如下所示,其中Pl(i=1,…,5)为各阶振型的特征 开始 根,数值解分别为1.875,4.694,7.855,10.996, 设定概率A,、层数m,初始值=1 1413=-引,≥3)四. 抽取N个服从分布∫x)的样本,并将样本 EI 对应的功能函数g)从小到大进行摔序 := NpA 2π (i=1,2,…,5) 取第pN个的功能函数值为临界值b 利用MSC.Nastran软件建立悬臂梁模型,将梁 F)=1-B 划分成50个单元,并计算前五阶固有频率,对应的 振型如图4所示,悬臂粱固有频率的Nastran解与解 F(F)--P(P)) ii+1 析解相比误差很小。 由落在F域的p,N个样本点出发,用MCMC抽取 N个服从分布F)的样本,将样本点对应的 功能函数(x)从小到大进行排序 取第pN个功能函数值为临界值6, 一阶振型 i=m? P(F.)=p: 采用式(④(Q估计应的 统计矩及统计矩灵敏度 二阶振型 图2 基于MCMC的分层抽样法的统计矩和灵敏度分析 的流程图 3算例分析 3.1等截面悬臂梁 考虑如图3所示的等截面悬臂梁的固有频率分 析。考虑其弹性模量E、材料密度P、梁的长度l和梁截 面半径R为随机变量,分别考虑两种情况,情况一:随 机变量均服从相互独立的正态分布,它们的均值分别 为200GPa,7800kg/m3,1m,2cm,变异系数分别为 0.05,0.05,0.01,0.01:情况二:E,p仍服从正态分 四阶振型 布,参量不变,而1,A服从均匀分布,它们的有效取值 区间分别为[0.95m,1.05m]和[1.9cm,2.1cm]. 对于等截面悬臂梁结构,其固有频率能给出解 五阶振型 图3等截面悬臂粱示意图 图4等截面悬臂梁的前五阶振型图示 万方数据
第2期 宋述芳,等:随机结构动力特征的统计矩及灵敏度分析研究 135 度分析,其具体的实现流程图参见图2。 图2基于MCMC的分层抽样法的统计矩和灵敏度分析 的流程图 3算例分析 3.1等截面悬臂梁 考虑如图3所示的等截面悬臂梁的固有频率分 析。考虑其弹性模量E、材料密度P、梁的长度Z和梁截 面半径R为随机变量,分别考虑两种情况,情况一:随 机变量均服从相互独立的正态分布,它们的均值分别 为200 GPa,7 800 kg/m3,1 m,2 cm,变异系数分别为 o.05,o.05,o.01,o.01;情况二:E,』D仍服从正态分 布,参量不变,而,,A服从均匀分布,它们的有效取值 区间分别为[o.95 m,1.05 m]和[1.9 cm,2.1 cm]。 对于等截面悬臂梁结构,其固有频率能给出解 图3等截面悬臂梁示意图 析的形式,下面列出前五阶固有频率的解析表达式 如下所示,其中展,(i=l,…,5)为各阶振型的特征 根,数值解分别为1.875,4.694,7.855,10.996, , , 1 I I[10】 14.137l届z士I i一去l耳,(i≥3)I . 所 嘶2一 利用MSC.Nastran软件建立悬臂梁模型,将梁 划分成50个单元,并计算前五阶固有频率,对应的 振型如图4所示。悬臂梁固有频率的Nastran解与解 析解相比误差很小。 】, zL z 一阶振型 y \ zL x 二阶振型 lr zL z 三阶振型 y zL x 四阶振型 么j弓二V zL x 五阶振型 图4等截面悬臂梁的前五阶振型图示 万方数据
136 振动工程学报 第24卷 下面采用MCMC分层抽样法结合Nastran软 的引入对自振频率的标准差的影响逐渐明显起来。 件计算各阶频率响应函数的均值和标准差,并与 采用MCMC分层抽样法和Monte Carlo模拟分 Monte Carlo模拟做了比较(Monte Carlo调用了自 别对情况一进行固有频率的均值和标准差对变量均 振频率的显式表达式),Monte Carlo模拟次数为l03 值的灵敏度分析,其结果列于表2。表2表明矩估计 次(表中记为MCS),本文方法调用功能函数的次数 方法的灵敏度结果具有很高的精度,并且基于矩估 为30X10000次(其中30为设定的层数,即m=30)。 计的灵敏度分析是在估计频率的统计矩的基础上进 表1表明本文方法与Monte Carlo模拟的结果非常 行的,不会增加太多的计算量,为了比较悬臂梁中各 接近,误差均在可接受范围内,并且基于MCMC分 随机参数的重要性,需要将表2中的灵敏度值标准 层抽样法对非正态变量也有很好的适用性。由表1 可以看出均匀分布的引入对固有频率的均值的影响 化,即灵敏度因子S路-歌·经和S%=最·总, .,结 不大,但随着悬臂粱固有频率阶数的增大,均匀分布 果如表3所示。 表1前五阶频率的统计矩 顿率阶数 1 2 3 4 5 情况一:均值 本文方法 28.253 177.091 487.474 972.082 1606.168 MCS 28.359 177.737 497.718 975.350 1612.151 本文方法 28.137 177.236 496,316 967.715 1607.610 情况二:均值 MCS 28.424 178.109 498.834 977.493 1615.776 本文方法 1.264 7.901 22.079 43.556 72.319 情况一:标准差 MCS 1.190 7.457 20.881 40.919 67.635 …本文方法 2.018 12.912 36.380 71.108 117.534 情况二:标准差 MCS 2.095 13.150 36.816 72.112 119.180 表2 固有频率的均值和标准差对变量均值的灵敏度 阶数 方法 弘 L at。 0 2b。 来 本文方法7.050X10-”-1.771×10-1.331×103 -55.384 8.529X10--1.317×10-4 55.443 -2.662 MCS7.109×10-1-1.823X10-1.411×10 -56.752 8.529×10--1.317×10-4 55.443 -2.662 -0.01127 9.367X103 -3.421×1025.589×10-12-8.026×10-4 343.133 -15.806 2 本文方法4.368×10-10 MCS 4.456X10-10 -0.01143 8.845X103 -3.557X1025.359X10-2-8.254×10-4 347,739 -16.692 本文方法1.220X10-· -0.03300 2.421X10 -9.824×1021.455×10-11-2.125×10-10.9219×103 -46.857 3 MCS 1.248X10-9 -0.03199 2.477×10° -9.960X1021.501×10-1-2.311×10-10.9738×103 -46.742 本文方法2.292×10。 -0.06219 4.789X10 -1.902×1032.787×10-1-4.542×10-11.906×10 -92.548 MCS2.445×10- -0.06269 4.854X10 -1.952X1032.934X10-11.-4.528X10-31.907×102 -91.541 本文方法3.912×10~” -0.1050 8.256×10-3.1612×1034.630X10-1-7.575×10-33.357X103 -153.495 MCS 4.041×10-。 -0.1036 8.023X10-3.2262X1034.849×10-1-7.484X10-3.152×103 -151.307 表3说明了两个问题:(1)杆长对频率的影响程 3.2带圆盘的轴系统 度是最大的,其次是梁的截面半径,而弹性模量和材 料密度的均值对频率的影响小且基本相同:(2)弹性 回转体的轴两端简支,圆盘在轴的中间固定,将 模量和梁截面半径的增加会使梁的自振频率加大, 轴竖放以略去回转体自重的影响。设圆盘质量为m, 而其余变量的增加会减小自振频率。悬跨粱自振频 轴看作是弹簧系数为k的复原元件,其质量不计:静 率的解析表达式也可证明以上的两个观点。 止时轴为一直线,其中心线为OO轴,圆盘的几何中 表3自振频率的标准化灵做度 心A在中心线上:G为回转重心,偏心距为e。回转体 在作回转振动时,轴的挠度为r=OA,偏心距e= 0.5014 -0.50140.9953 -2.001 AG,在轴心A上沿向心的方向作用有弹簧力F一kr, 在重心G上有沿离心方向作用的离心惯性力F,= 0.1434 -0.8631 0.9320 -2.237 m(r十e)u(u为回转轴的角速度)。 万方数据
振 动 工 程 学 报 第24卷 下面采用MCMC分层抽样法结合Nastran软 件计算各阶频率响应函数的均值和标准差,并与 Monte Carlo模拟做了比较(Monte Carlo调用了自 振频率的显式表达式),Monte Carlo模拟次数为108 次(表中记为MCS),本文方法调用功能函数的次数 为30×10 ooo次(其中30为设定的层数,即珊=30)。 表1表明本文方法与Monte carlo模拟的结果非常 接近,误差均在可接受范围内,并且基于MCMC分 层抽样法对非正态变量也有很好的适用性。由表1 可以看出均匀分布的引入对固有频率的均值的影响 不大,但随着悬臂梁固有频率阶数的增大,均匀分布 的引入对自振频率的标准差的影响逐渐明显起来。 采用MCMC分层抽样法和Monte Carlo模拟分 别对情况一进行固有频率的均值和标准差对变量均 值的灵敏度分析,其结果列于表2。表2表明矩估计 方法的灵敏度结果具有很高的精度,并且基于矩估 计的灵敏度分析是在估计频率的统计矩的基础上进 行的,不会增加太多的计算量。为了比较悬臂梁中各 随机参数的重要性,需要将表2中的灵敏度值标准 化,即灵敏度因子s≈=豢·笼和s弩=象‘瓮,结 果如表3所示。 衰l前五阶频率的统计矩 频率阶数 1 2 3 4 情况一:均值…二号:呈萋……-冀毫蓦……一;舅j;嚣……一i;≥;嚣……一;凳j:薰……}詈要譬誓… t青况二:均值…·j;÷!i』:i誉……一·冀:·:薹………;;ij;i:……-一i;;ji::……·一;;;:·i:i……·;·{;;j·;冀… 情鼽标准差本瑟法…-篙}……篡}…一.蠢导…一篇》…·黧》· 情况二:标准差…二!j:呈登……一}器}……一冀冀瑟………冀薯冀………凳等矍……一;;ij;嚣…- 表2固有频率的均值和标准差对变量均值的灵敏度 表3说明了两个问题:(1)杆长对频率的影响程 度是最大的,其次是梁的截面半径,而弹性模量和材 料密度的均值对频率的影响小且基本相同;(2)弹性 模量和梁截面半径的增加会使梁的自振频率加大, 而其余变量的增加会减小自振频率。悬臂梁自振频 率的解析表达式也可证明以上的两个观点。 裘3自振频率的标准化灵敏度 兰釜 兰窆 兰兰 兰釜 O.501 4 一O.50l 4 O.995 3 —2.001 翌 壁 翌 壁 O.143 4 一O.863 1 O.932 O 一2.237 3.2带圆盘的轴系统 回转体的轴两端简支,圆盘在轴的中间固定,将 轴竖放以略去回转体自重的影响。设圆盘质量为小, 轴看作是弹簧系数为是的复原元件,其质量不计;静 止时轴为一直线,其中心线为0—0轴,圆盘的几何中 心A在中心线上;G为回转重心,偏心距为e。回转体 在作回转振动时,轴的挠度为r=0A,偏心距P= AG,在轴心A上沿向心的方向作用有弹簧力F一打, 在重心G上有沿离心方向作用的离心惯性力凡= m(r+P)山2(山为回转轴的角速度)。 万方数据
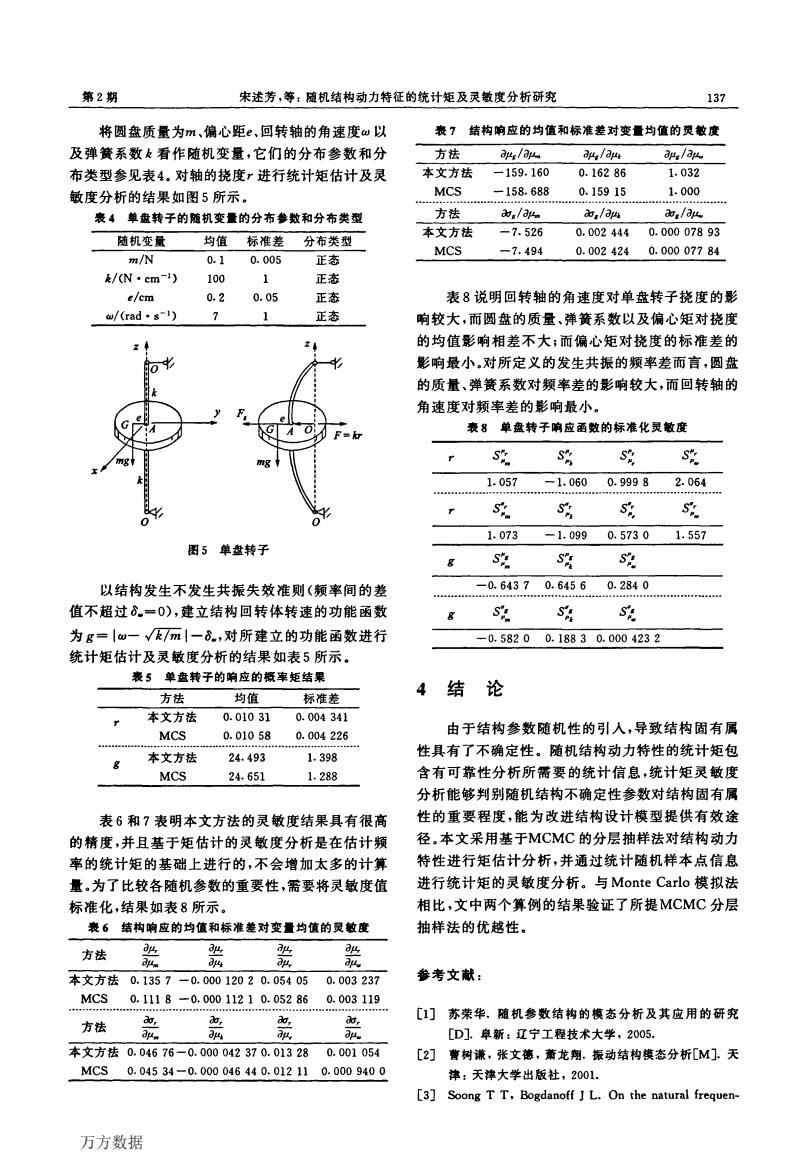
第2期 宋述芳,等:随机结构动力特征的统计矩及灵敏度分析研究 137 将圆盘质量为m、偏心距e、回转轴的角速度u以 表7 结构响应的均值和标准差对变量均值的灵敏度 及弹簧系数k看作随机变量,它们的分布参数和分 方法 a4./a 3ug/aue 4/a 布类型参见表4。对轴的挠度,进行统计矩估计及灵 本文方法 -159.160 0.16286 1.032 敏度分析的结果如图5所示。 MCS -158.688 0.15915 1.000 表4单盘转子的随机变量的分布参数和分布类型 方法 ./a ,/a adg/ou 本文方法 -7.526 0.002444 0.00007893 随机变量 均值标准差 分布类型 MCS -7.494 0.002424 0.00007784 m/N 0.10.005 正态 e/(N·cm-1) 100 1 正态 e/cm 0.2 0.05 正态 表8说明回转轴的角速度对单盘转子挠度的影 u/(rad·s-l) 7 1 正态 响较大,而圆盘的质量、弹簧系数以及偏心矩对挠度 的均值影响相差不大;而偏心矩对挠度的标准差的 0 影响最小,对所定义的发生共振的频率差而言,圆盘 的质量、弹簧系数对频率差的影响较大,而回转轴的 角速度对频率差的影响最小。 表8单盘转子响应函数的标准化灵敏度 S S S S* 1.057 -1.060 0.9998 2.064 r s 9 S S 1.073 -1.0990.5730 1.557 图5单盘转子 S Sh S 以结构发生不发生共振失效准则(频率间的差 -0.64370.64560.2840 值不超过6.=0),建立结构回转体转速的功能函数 S % S 为g=|w一√/m一6.,对所建立的功能函数进行 -0.58200.18830.0004232 统计矩估计及灵敏度分析的结果如表5所示。 表5单盘转子的响应的概率矩结果 4 方法 均值 标准差 结 论 《 本文方法 0.01031 0.004341 MCS 0.01058 0.004226 由于结构参数随机性的引入,导致结构固有属 本文方祛 24.493 1.398 性具有了不确定性。随机结构动力特性的统计矩包 MCS 24.651 1.288 含有可靠性分析所需要的统计信息,统计矩灵敏度 分析能够判别随机结构不确定性参数对结构固有属 表6和7表明本文方法的灵敏度结果具有很高 性的重要程度,能为改进结构设计模型提供有效途 的精度,并且基于矩估计的灵敏度分析是在估计频 径,本文采用基于MCMC的分层抽样法对结构动力 率的统计矩的基础上进行的,不会增加太多的计算 特性进行矩估计分析,并通过统计随机样本点信息 量,为了比较各随机参数的重要性,需要将灵敏度值 进行统计矩的灵敏度分析。与Monte Carlo模拟法 标准化,结果如表8所示。 相比,文中两个算例的结果验证了所提MCMC分层 表6结构响应的均值和标准差对变量均值的灵敏度 抽样法的优越性。 方法 班 弘 班 弘 。 4 a a 本文方法0.1357-0.00012020.054050.003237 参考文献: MCS 0.1118-0.00011210.052860.003119 方法 do, , dd, [1]苏荣华.随机参数结构的模态分析及其应用的研究 μ。 34 职 0μ [D].单新:辽宁工程技术大学,2005. 本文方法0.04676-0.000042370.013280.001054 [2]曹树谦,张文德,萧龙翔.振动结构模态分析[M].天 MCS0.04534-0.000046440.012110.0009400 津:天津大学出版社,2001. [3]Soong TT,Bogdanoff J L.On the natural frequen- 万方数据
第2期 宋述芳,等:随机结构动力特征的统计矩及灵敏度分析研究 137 将圆盘质量为优、偏心距e、回转轴的角速度cc,以 及弹簧系数五看作随机变量,它们的分布参数和分 布类型参见表4。对轴的挠度,.进行统计矩估计及灵 敏度分析的结果如图5所示。 衰4单盘转子的随机变量的分布参数和分布类型 图5单盘转子 以结构发生不发生共振失效准则(频率间的差 值不超过乱=o),建立结构回转体转速的功能函数 为g=I叫一厮I一乱,对所建立的功能函数进行 统计矩估计及灵敏度分析的结果如表5所示。 表5单盘转子的响应的概率矩结果 方法 均值 标准差 r 本文方法 o·olo 31 O-004 34l MCS 0.010 58 0.004 226 g 本文方法 24·493 1·398 MCS 24.651 1.288 表6和7表明本文方法的灵敏度结果具有很高 的精度,并且基于矩估计的灵敏度分析是在估计频 率的统计矩的基础上进行的,不会增加太多的计算 量。为了比较各随机参数的重要性,需要将灵敏度值 标准化,结果如表8所示。 袭6结构响应的均值和标准差对变量均值的灵敏度 方法 薏 豢 篆 差 本文方法o.135 7一o.ooo 120 2 o.054 05 o.003 237 MCS 0.1ll 8一O.OOO 112 1 O.052 86 O.003 119 方法 薏 襄 蓑 蓑 本文方法o.046 76一O.000 042 37 0.013 28 o.001 054 MCS O.045 34一O.ooO 046 44 0.012 ll O.ooO 940 O 表7结构响应的均值和标准差对变量均值的灵敏度 南法 a≯g伯‰ a弘sfa池 a昝I}a‰ 本文方法 一159.160 O.162 86 1.032 MCS 一158.688 O.159 15 1.OOO 贺法 抽|fa‰ 硇I}a№ 硇|}a‰ 表8说明回转轴的角速度对单盘转子挠度的影 响较大,而圆盘的质量、弹簧系数以及偏心矩对挠度 的均值影响相差不大;而偏心矩对挠度的标准差的 影响最小。对所定义的发生共振的频率差而言,圆盘 的质量、弹簧系数对频率差的影响较大,而回转轴的 角速度对频率差的影响最小。 表8单盘转子响应函数的标准化灵敏度 r s芝 s乏 sZ sZ 1.057 —1.060 O.999 8 2.064 ,. 瞳 sZ 殴 s乞 一O.643 7 O.645 6 0.284 O g s乏 s二: s乏 4 结 论 由于结构参数随机性的引入,导致结构固有属 性具有了不确定性。随机结构动力特性的统计矩包 含有可靠性分析所需要的统计信息,统计矩灵敏度 分析能够判别随机结构不确定性参数对结构固有属 性的重要程度,能为改进结构设计模型提供有效途 径。本文采用基于MCMC的分层抽样法对结构动力 特性进行矩估计分析,并通过统计随机样本点信息 进行统计矩的灵敏度分析。与Monte Carlo模拟法 相比,文中两个算例的结果验证了所提MCMC分层 抽样法的优越性。 参考文献: [1]苏荣华。随机参数结构的模态分析及其应用的研究 [D].阜新:辽宁工程技术大学,2005. [2] 曹树谦,张文德.萧龙翔.振动结构模态分析[M].天 津:天津大学出版社,2001. [3] Soong T T,Bogdano“J L.0n the natural frequen- 万方数据