
第18卷4期 应用基础与工程科学学报 Vol.18,No.4 2010年8月 JOURNAL OF BASIC SCIENCE AND ENGINEERING August 2010 文章编号:10050930(2010)040695-10 中图分类号:X830.2 文献标识码:A doi:10.3969/5.isn.1005-0930.2010.04.017 基于伴随方程和MCMC方法的 室内污染源反演模型研究 郭少冬12,杨锐,苏国锋,张辉 (1.清华大学工程物理系,公共安全研究中心,北京100084;2.北京应用物理与计算数学研究所,北京100094) 摘要:研究了室内污染彻扩散后的源反演方法.通过数值求解浓度场的伴随方 程,并结合传感器测量信息,构造似然函数;利用基于贝叶斯推断理论的Markov Chain Monte Carlo(MCMC)抽样方法,对污染源的位置、强度的后验概率进行计 算,反演结果与污染源的真实参数吻合.该方法与传统的室内污染物反演方法相 比,极大地降低了计算量.此外,还讨论了传感器性能对结果的影响,研究表明传 感器误差概率分布越平坦,污染源反演信息的不确定度越大;而过低的测量灵敏 度,则会导致反演结果呈现多个局部极值点的特性 关键词:室内污染源反演;贝叶斯推断:伴随方程:计算流体力学 公用建筑内相对密闭,人员密集,一旦出现有毒气体泄漏或遭受生化袭击,有毒气体 会在通风气流等作用下迅速扩散,带来巨大威胁.而能否迅速准确地掌握释放源的相关信 息,对于应急疏散和处置策略的制定十分重要. 源项反演目前主要有直接求解、优化方法和概率方法等.直接求解方法通过构造控制 微分方程的反问题,利用正则变换,将其转化为适定的问题,进行解析或数值求解.解析解 的研究主要集中在热传导领域)和大气污染问题).随着C℉D算法的成熟,反演的数值 方法也开始得到发展.Skaggs[)采用拟可逆(Quasi-Reveraibility)方法在一维对流扩散方程 中引人了四阶耗散项抑制振荡,解决了稳定性问题;Bagtzoglou),Zhang's)分别将此方法 用于地下水污染源、室内污染源的定位研究.另一类重要的反演方法是优化方法, Skaggst6)和Alapati1分别采用正则优化方法和最小二乘法对地下水污染源进行参数反演 研究 贝叶斯概率方法因其可直接引入测量误差和数值模型误差的影响,受到了研究者广 泛的关注.在城区有害气体扩散和水污染的源参数反演方面,Kats⑧]、朱嵩]等采用 Markov Chain Monte Carlo(MCMC)抽样方法取得了一系列的研究成果.根据伴随算子的线 性性质,刘峰等o)发展了一种针对任意污染源的风险函数计算方法.Liu和Zhai1山将伴 收稿日期:2008-1009:修订日期:2009-05-19 基金项目:国家自然科学基金(50804027) 作者简介:郭少冬(1982一),男,博士,助理研究员. 通迅作者:杨锐(1976一),男,博士,副教授.E-mail:yang@tsinghua.cdu.cn 万方数据
第18卷4期 2010年8月 应用基础与工程科学学报 JOURNAL OF BASIC SCIENCE AND ENGINEERING V01.18.No.4 August 2010 文章编号:1005-0930(2010)04-0695-10 中图分类号:X830.2 文献标识码:A doi:10.3969/j.i啪.1005-0930.2010.04.017 基于伴随方程和MCMC方法的 室内污染源反演模型研究 郭少冬1’2, 杨 锐1, 苏国锋1, 张辉1 (1.清华大学工程物理系,公共安全研究中心,北京100084;2.北京应用物理与计算数学研究所,北京100094) 摘要:研究了室内污染物扩散后的源反演方法.通过数值求解浓度场的伴随方 程,并结合传感器测量信息,构造似然函数;利用基于贝叶斯推断理论的Markov Chain Monte Carlo(MCMC)抽样方法,对污染源的位置、强度的后验概率进行计 算,反演结果与污染源的真实参数吻合.该方法与传统的室内污染物反演方法相 比,极大地降低了计算量.此外,还讨论了传感器性能对结果的影响,研究表明传 感器误差概率分布越平坦,污染源反演信息的不确定度越大;而过低的测量灵敏 度,则会导致反演结果呈现多个局部极值点的特性. 关键词:室内污染源反演;贝叶斯推断;伴随方程;计算流体力学 公用建筑内相对密闭,人员密集,一旦出现有毒气体泄漏或遭受生化袭击,有毒气体 会在通风气流等作用下迅速扩散,带来巨大威胁.而能否迅速准确地掌握释放源的相关信 息,对于应急疏散和处置策略的制定十分重要. 源项反演目前主要有直接求解、优化方法和概率方法等.直接求解方法通过构造控制 微分方程的反问题,利用正则变换,将其转化为适定的问题,进行解析或数值求解.解析解 的研究主要集中在热传导领域¨1和大气污染问题【2 J.随着CFD算法的成熟,反演的数值 方法也开始得到发展.Skaggs”1采用拟可逆(Quasi-Reversibility)方法在一维对流扩散方程 中引入了四阶耗散项抑制振荡,解决了稳定性问题;BagtzoglOUl4J,Zhang【5 o分别将此方法 用于地下水污染源、室内污染源的定位研究.另一类重要的反演方法是优化方法, Skaggs∞1和Alapati【7j分别采用正则优化方法和最小二乘法对地下水污染源进行参数反演 研究. 贝叶斯概率方法因其可直接引入测量误差和数值模型误差的影响,受到了研究者广 泛的关注.在城区有害气体扩散和水污染的源参数反演方面,Keats【8 J、朱嵩一。等采用 Markov Chain Monte Carlo(MCMC)抽样方法取得了一系列的研究成果.根据伴随算子的线 性性质,刘峰等¨叫发展了一种针对任意污染源的风险函数计算方法.uu和Zhai 011]将伴 收稿日期:2008.10-09;修订日期:2009-05—19 基金项目:国家自然科学基金(50804027) 作者简介:郭少冬(1982一),男,博士,助理研究员. 通迅作者:杨锐(1976一),男,博士,副教授.E-mail:ryang@tsinghua.edu.Cll 万方数据

696 应用基础与工程科学学报 Vol.18 随方法应用于室内空气污染源的定位,数值求解后向概率密度输运方程,并通过在全参数 空间内积分,直接计算源位置的后验概率.该研究是在释放源强已知的情况下,对释放源 位置进行反演,因此可采用全参数空间的积分获得后验分布,计算量并不大,但当释放源 强度也未知时,若直接计算后验概率会涉及高维的积分,计算效率会显著降低, 本文采用MCMC抽样算法,产生一组收敛于后验分布的抽样点,并对其进行统计分 析,获得室内污染源位置和强度的概率信息.同时,通过构造浓度场的伴随方程,解决 MCMC方法需要大量正向计算的困难.此外,本文还对传感器测量误差分布和测量范围对 反演结果的影响进行了分析讨论 1模型描述 1.1贝叶斯推断 根据贝叶斯理论 p(x)=(YI(p(1x).p(x) P() (1) 其中X为污染源的相关参数,是需要进行反演的随机变量:Y为传感器的测量信息或其它 观测信息;(X)为源项参数X的先验分布,可以根据事先对源项的已知信息和判断给 定;p(Y1)为给定源项参数X下,数据Y的条件概率,称为似然概率,它的确定通常需 要综合考虑传感器的相关特性和正向数值模拟的误差;(XIY)指在获取有关信息Y后, 源参数X的概率分布.当得到源参数X的后验分布后,就可以对该参数进行估计,从而实 现对污染源空间位置的定位和强度反演. 1.2测量误差与模型误差 传统的直接反演方法,通常假设传感器的测量结果和数值模型的预测是精确的.即使 考虑误差因素,也只是在求出源参数后,对结果进行扰动分析;而基于贝叶斯推断的概率 方法可以在反演模型本身引人传感器和数值模型的误差,对反演结果的不确定性进行分 析,进而给出一定置信概率下的置信区间. 设观测点的测量值为Y={Y,Y2,…,Y:,…,Y},数值正向模型在测量点的预测值为 F={F,F2,…,F,…,F},而实际理论值为T={T,T2,…,T,…,T},引人传感器测量值 与理论值的误差e:,Y:=T:+8:;正向数值模型预测值与理论值的误差e,F:(X)=T:() +e.通常这两种误差可近似认为服从高斯分布8)e~Gau(0,ci)和e:~Gau(0,c). 从而得到 ()p 2 (2) pTix,F)xep-(T)二FX)1 (3) 2o 假设两种误差相互独立,则 D-I0zi,Pne-g (4) 假设每个测量点相互独立,则得到似然概率 万方数据
应用基础与工程科学学报 V01.18 随方法应用于室内空气污染源的定位,数值求解后向概率密度输运方程,并通过在全参数 空间内积分,直接计算源位置的后验概率.该研究是在释放源强已知的情况下,对释放源 位置进行反演,因此可采用全参数空间的积分获得后验分布,计算量并不大,但当释放源 强度也未知时,若直接计算后验概率会涉及高维的积分,计算效率会显著降低. 本文采用MCMC抽样算法,产生一组收敛于后验分布的抽样点,并对其进行统计分 析,获得室内污染源位置和强度的概率信息.同时,通过构造浓度场的伴随方程,解决 MCMC方法需要大量正向计算的困难.此外,本文还对传感器测量误差分布和测量范围对 反演结果的影响进行了分析讨论. 1模型描述 1.1 贝叶斯推断 根据贝叶斯理论 p(x t玢:趔等弹,盟芘p(Yt x),p(x) (1) P~1, 其中x为污染源的相关参数,是需要进行反演的随机变量;Y为传感器的测量信息或其它 观测信息;p(X)为源项参数x的先验分布,可以根据事先对源项的已知信息和判断给 定;P(YI x)为给定源项参数x下,数据y的条件概率,称为似然概率,它的确定通常需 要综合考虑传感器的相关特性和正向数值模拟的误差;p(xI l,)指在获取有关信息y后, 源参数x的概率分布.当得到源参数x的后验分布后,就可以对该参数进行估计,从而实 现对污染源空间位置的定位和强度反演. 1.2 测量误差与模型误差 传统的直接反演方法,通常假设传感器的测量结果和数值模型的预测是精确的.即使 考虑误差因素,也只是在求出源参数后,对结果进行扰动分析;而基于贝叶斯推断的概率 方法可以在反演模型本身引入传感器和数值模型的误差,对反演结果的不确定性进行分 析,进而给出一定置信概率下的置信区间. 设观测点的测量值为Y={L,y2,…,yi,…,K},数值正向模型在测量点的预测值为 F={F。,R,…,E,…,凡},而实际理论值为T={L,疋,…,正,…,瓦},引入传感器测量值 与理论值的误差反,K=t+岛;正向数值模型预测值与理论值的误差e;,Fi(x)=正(X) +e;.通常这两种误差可近似认为服从高斯分布哺1B—Gau(O,盯,2.i)和e‘~C,au(O,%2i). 从而得到 p(yi I正,x)茁exp{一掣 p(t Ix,F)。c exp{一生堡垒铲) 假设两种误差相互独立,则 则㈨=如(m剐驰胂…p{-端) 假设每个测量点相互独立,则得到似然概率 (2) (3) (4) 万方数据

No.4 郭少冬等:基于伴随方程和MCMC方法的室内污染源反演模型研究 697 p(1=ip(g10e-含2+ (F(x)-Y) (5) 1.3伴随方程与正问题数值方法 计算后验概率时,需要考虑全参数空间或该空间的许多抽样点,传统的方法经常需要 对所有可能的源参数进行正向数值模拟,求解稳态N-S方程和组分扩散方程(6),得到测 量点处的浓度值F(X)· r.VC-V·(D7C)=Sxen l6.c.7C.n=0 (6) XEan 计算量是非常巨大的.考虑到传感器的数量通常较少,而每一次的正向模拟也只是为得到 有限传感器位置的浓度值,因此可利用伴随算子的性质,求解与原浓度场对应的伴随浓 度场) r-7·7G-7·(D7G)=(X-X') X∈n 1b.c.CV.i+DVG.n=0 (7) Xean 根据 C(X)={C(x)8(X-X')d (8) 将式(7)代入,并根据场论和不可压缩条件有 c(X)=[C(-v.Vc-V.(DVC))dx =-A[-cC+Gv·(DvC)+7·(CGW+7·(cDVG) -V·(DGVC)]dX (9) 代人方程(6),有 C(x')=[GS-V·(CG-7·(cD7G)+V·(DGVC)]d (10) 根据高斯定理,有 C(X)=[csax-ccv.idr-cDvc.idr+Dcvc.idr (11) 代入边界条件VC·元=0,G·元+DVG·n=0(Xen),可得到 C(X)=[G(X,X')S(X)dx (12) 传统方法中,当需要求解在n个不同位置(X,Xa,…,X.,…,Xm)污染源,扩散到某个传 感器位置X'处的浓度值时,需要进行次正向数值模拟,得到同一个点处的浓度值.而利 用上述关系,只需将污染源放置在该空间点X′处,强度取一个单位,求解一次伴随方程 (方程(7)是点源连续泄漏问题),得到伴随浓度场G(X,X),进而利用方程(12),即可得 到同一空间点处在不同源条件下的浓度值. 当污染源为点源时,S=Q·8(X-X,),可进一步得到 c(X)[Q.G(X,X')8(X-x,)dx Q.c(X.X) (13) 因此利用求解一次伴随方程获得的浓度场,即可获得个不同源参数下在同一传感器位 万方数据
No.4 郭少冬等:基于伴随方程和MCMC方法的室内污染源反演模型研究 697 p(yI x)=lkIp(y:l x)。c exp{一毫嬲) (5) 1.3伴随方程与正问题数值方法 计算后验概率时,需要考虑全参数空间或该空间的许多抽样点,传统的方法经常需要 对所有可能的源参数进行正向数值模拟,求解稳态N·S方程和组分扩散方程(6),得到测 量点处的浓度值F(X’). ∥Vc一∑。(DVc)=s x∈Q (6) 1 b.c.VC.元=0 X∈aQ ¨7 计算量是非常巨大的.考虑到传感器的数量通常较少,而每一次的正向模拟也只是为得到 有限传感器位置的浓度值,因此可利用伴随算子的性质,求解与原浓度场对应的伴随浓 度场”1 f一矿·VG—V·(DVG)=6(X—X’) Z∈Q ,,、 1 b.c.G『矿.五+DvG·矗=0 x E aQ 、。7 根据 c(x’)=f c(x)6(X—X’)栅 (8) 将式(7)代入,并根据场论和不可压缩条件有 c(石’)=I.C(一矿·VG—V·(DVG))dx =一f.[一G矿Vc+GV·(DVc)+V·(cG矿)+V·(CDVG) 一V·(DGVC)]dX (9) 代入方程(6),有 C(X’)=f.[船一V·(COP)一V·(CDVG)+V·(DGVC)]dX (10) 根据高斯定理,有 C(X’)=f GSdX—f cG矿·元d厂一f.CDVG·矗d,+f DGVC·矗d厂 (11) Jn Jan Jdn J#O 代入边界条件VC·元=0,西·完+DVG·高=o(x∈aQ),可得到 c(X’)=J G(x,x’)s(x)锻 (12) 传统方法中,当需要求解在n个不同位置(L,Xa,…,如,…,五。)污染源,扩散到某个传 感器位置x’处的浓度值时,需要进行n次正向数值模拟,得到同一个点处的浓度值.而利 用上述关系,只需将污染源放置在该空间点X’处,强度取一个单位,求解一次伴随方程 (方程(7)是点源连续泄漏问题),得到伴随浓度场G(x,x7),进而利用方程(12),即可得 到同一空间点处在不同源条件下的浓度值. 当污染源为点源时,S=Q·8(x一置),可进一步得到 C(X’)=J。Q。a(X,X’)艿(x一置)dX=Q‘c(墨,X’) (13) 因此利用求解一次伴随方程获得的浓度场,即可获得n个不同源参数下在同一传感器位 万方数据

698 应用基础与工程科学学报 Vol.18 置处的浓度值 (QG(XX'),02G(X2,X).QG(Xx),.0G(XX')) 正问题的计算需要求解不可压缩Navier-Stokes方程组和伴随方程(7).由于组分源 对环境流场的影响较小,因此本文假定处于相同位置而不同的泄漏源强度,其速度场保持 不变.计算中将连续方程、动量方程与浓度扩散方程分离求解,即先求解速度和压力场,在 其收敛后,将速度场和湍流粘性系数代入伴随方程(7),求解浓度场。数值格式采用基于 有限体积交错网格的SIMPLE算法,湍流模型采用标准k-ε模型. 1.4MCMC算法 公式(1)确定了后验概率密度的计算方法,其中分母为 n=jr1x(x0en-言0+品 、(F(X)-Y)21 (14) 该积分在整个参数空间上进行,对于参数空间维数较低时,其计算量尚可接受,但实际中 通常需要估计的源参数都是多维向量,即使采用传统的Monte Carlo积分方法,计算这种 多维积分效率也很低 注意到后验概率正比于似然概率(5)和先验分布的乘积,因此可采用MCMC方法,通 过合理的构造转移概率,直接产生一组分布概率为后验概率的随机抽样点,这些抽样点构 成一条马尔可夫链,该马氏链收敛后的静态分布即为所需的后验分布.满足上述要求的转 移概率和MCMC抽样方法主要有Gibbs算法,Metropolis算法、Metropolis--Hasting算法等. 本文采用结合Metropolis-Hasting算法的MCMC抽样,具体步骤见文献[I2]. 2室内污染源反演问题研究 2.1场景描述 Liu和Zhai研究了室内污染源的二维定位问题,本文选取类似的场景,如图1所 示,一个4m高,10m长的房间内有6个人和6台计算机及办公桌,左侧1.5一1.8m高处 有一空调送风口,以1m/s的速度水平送风,房间顶棚有一通风口,与外界进行质量交换. 在房间顶部通风口两侧对称地安装有两个传感器.污染源位于人头部的前方,位置坐标 (1.95m,1.25m),坐标原点取在房间的左下角.污染源强度为0.8kg/m3·8. 出口 传感器十传感器 6.7E-0.2 3.3E-03 1.7E-04 送风▣ 8.2E-06 4.1E-07 2.0E-08 1.0E-09 图1房间简化图与稳态浓度场 Fig.1 simplified diagram of the room and steady concentration field 万方数据
应用基础与工程科学学报 VDl.18 置处的浓度值 (Q,。G(置。,X7),Q也G(X,2,X’),…,Q,IG(置。,X’),…,Q,。G(置。,X’)) 正问题的计算需要求解不可压缩Navier—Stokes方程组和伴随方程(7).由于组分源 对环境流场的影响较小,因此本文假定处于相同位置而不同的泄漏源强度,其速度场保持 不变.计算中将连续方程、动量方程与浓度扩散方程分离求解,即先求解速度和压力场,在 其收敛后,将速度场和湍流粘性系数代入伴随方程(7),求解浓度场。数值格式采用基于 有限体积交错网格的SIMPLE算法,湍流模型采用标准k-8模型. 1.4 MCMC算法 公式(1)确定了后验概率密度的计算方法,其中分母为 p(1,)=』p(1,I x)p(x)d.Y。c-f exp{一圭i=1{粼)p(x)dx(14) 该积分在整个参数空间上进行,对于参数空间维数较低时,其计算量尚可接受,但实际中 通常需要估计的源参数都是多维向量,即使采用传统的Monte Carlo积分方法,计算这种 多维积分效率也很低. 注意到后验概率正比于似然概率(5)和先验分布的乘积,因此可采用MCMC方法,通 过合理的构造转移概率,直接产生一组分布概率为后验概率的随机抽样点,这些抽样点构 成一条马尔可夫链,该马氏链收敛后的静态分布即为所需的后验分布.满足上述要求的转 移概率和MCMC抽样方法主要有Gibbs算法,Metropolis算法、Metropolis—Hasting算法等. 本文采用结合Metropolis—Hasting算法的MCMC抽样,具体步骤见文献[12]. 2室内污染源反演问题研究 2.1场景描述 Ⅱu和Zhai[I¨研究了室内污染源的二维定位问题,本文选取类似的场景,如图1所 示,一个4m高,10m长的房间内有6个人和6台计算机及办公桌,左侧1.5一1.8m高处 有一空调送风口,以lm/s的速度水平送风,房间顶棚有一通风口,与外界进行质量交换. 在房间顶部通风13两侧对称地安装有两个传感器.污染源位于人头部的前方,位置坐标 (1.95m,1.25m),坐标原点取在房间的左下角.污染源强度为0.8kg/m3·8. 图1 房间简化图与稳态浓度场 Fig.1 simplified diagram of the loom and steady concentration field 万方数据
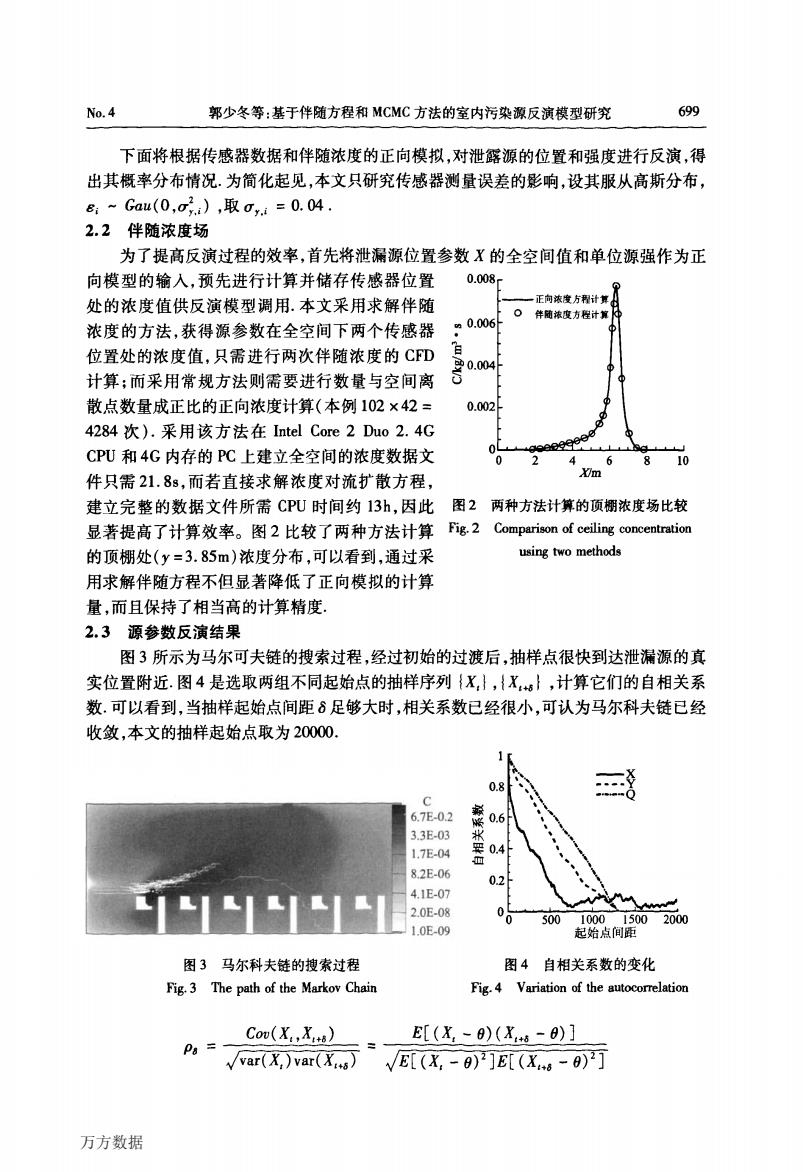
No.4 郭少冬等:基于伴随方程和MCMC方法的室内污染源反演模型研究 699 下面将根据传感器数据和伴随浓度的正向模拟,对泄露源的位置和强度进行反演,得 出其概率分布情况.为简化起见,本文只研究传感器测量误差的影响,设其服从高斯分布, &:~Gau(0,oi),取oi=0.04. 2.2伴随浓度场 为了提高反演过程的效率,首先将泄漏源位置参数X的全空间值和单位源强作为正 向模型的输入,预先进行计算并储存传感器位置 0.008 处的浓度值供反演模型调用.本文采用求解伴随 一正向浓发方程计算 n0.006 口伴随浓度方程计算 浓度的方法,获得源参数在全空间下两个传感器 位置处的浓度值,只需进行两次伴随浓度的CFD 计算:而采用常规方法则需要进行数量与空间离 散点数量成正比的正向浓度计算(本例102×42= 0.002 4284次).采用该方法在Intel Core2Duo2.4G CPU和4G内存的P℃上建立全空间的浓度数据文 e9e9 4 6 810 件只需21.8s,而若直接求解浓度对流扩散方程, m 建立完整的数据文件所需CPU时间约13h,因此图2两种方法计算的顶棚浓度场比较 显著提高了计算效率。图2比较了两种方法计算Fig2 Comparison of ceiing concentration 的顶棚处(y=3.85m)浓度分布,可以看到,通过采 using two methods 用求解伴随方程不但显著降低了正向模拟的计算 量,而且保持了相当高的计算精度. 2.3源参数反演结果 图3所示为马尔可夫链的搜索过程,经过初始的过渡后,抽样点很快到达泄漏源的真 实位置附近.图4是选取两组不同起始点的抽样序列{X,},{X,s},计算它们的自相关系 数.可以看到,当抽样起始点间距8足够大时,相关系数已经很小,可认为马尔科夫链已经 收敛,本文的抽样起始点取为20000 0.8 6.7E-0.2 0.6 3.3E-03 1.7E-04 0.4 ◇ 82E-06 02 4.1E-07 2.0E-08 00 500100015002000 1.0E-09 起始点间距 图3马尔科夫链的搜索过程 图4自相关系数的变化 Fig.3 The path of the Markov Chain Fig.4 Variation of the autocorrelation Cov(X.,X) E[(X,-8)(X6-8)] Pa= √ar(X,)var(X6)√E[(X,-9)]E[(X-)] 万方数据
No.4 郭少冬等:基于伴随方程和MCMC方法的室内污染源反演模型研究 699 下面将根据传感器数据和伴随浓度的正向模拟,对泄露源的位置和强度进行反演,得 出其概率分布情况.为简化起见,本文只研究传感器测量误差的影响,设其服从高斯分布, 毋一Gau(O,盯y2.i),取盯y,f=0.04. 2.2伴随浓度场 为了提高反演过程的效率,首先将泄漏源位置参数x的全空间值和单位源强作为正 向模型的输入,预先进行计算并储存传感器位置 处的浓度值供反演模型调用.本文采用求解伴随 浓度的方法,获得源参数在全空间下两个传感器 位置处的浓度值,只需进行两次伴随浓度的CFD 计算;而采用常规方法则需要进行数量与空间离 O.008 。0.006 目 章o.004 U 散点数量成正比的正向浓度计算(本例102×42=0.002 4284次).采用该方法在Intel Core 2 Duo 2.4G 图3马尔科夫链的搜索过程 Fig.3 The path of the Markov Chin 图4自相关系数的变化 Fig.4 Variation of the autocorrelation Coy(X。,XⅢ) E[(置~0)(xm—o)] 几2蕊乖而示i 2万雨i丽丽ii两 万方数据