中值定理与导数应用 X2 X3 X4 X5 X6 X7 X8 图二
𝑥 𝑦 𝑥1 𝑥2 𝑥3 𝑥4 𝑂 𝑥5 图二 𝑥6 𝑥7 𝑥8

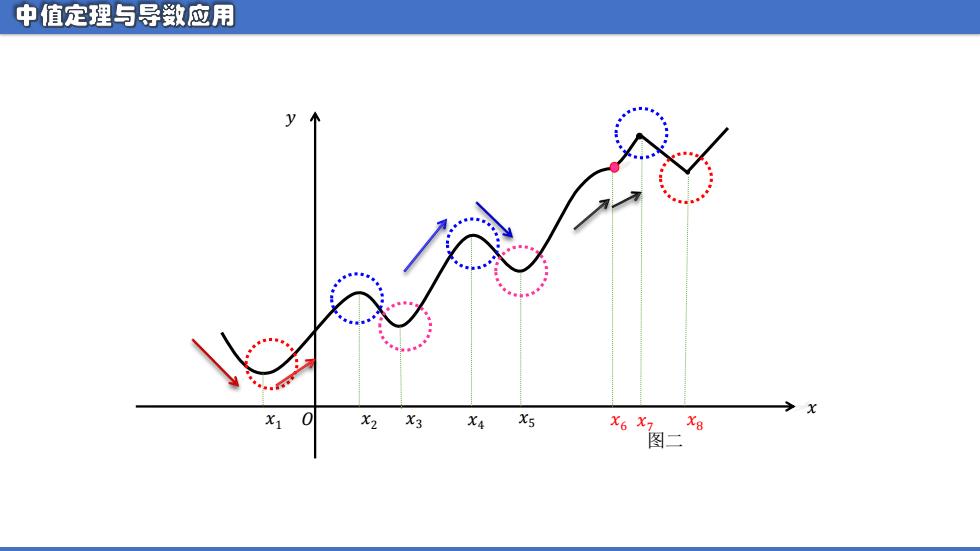
中值定理与导数应用 定理2:极值存在的第一充分条件: 设函数f(x)在点x处连续,在点x近旁可导(点x除外)。 (1)如果在x的左侧近旁,f'(x)>0,在x的右侧近旁,f'(x)<0, 则函数fx)在xo处取得极大值f(xo)。/个 (2)如果在x的左侧近旁,f'(x)<0,在xo的右侧近旁,'(x)>0, 则函数f(x)在x处取得极小值f(xo)。 (3)如果在x的左右两侧近旁,f'(x)同号,f(x)在xo处没有极值
定理2: 极值存在的第一充分条件: 设函数𝒇(𝒙)在点𝒙𝟎处连续,在点𝒙𝟎近旁可导(点𝒙𝟎除外)。 (1)如果在𝒙𝟎的左侧近旁,𝒇′(𝒙) > 𝟎,在𝒙𝟎的右侧近旁,𝒇′(𝒙) < 𝟎, 则函数𝒇(𝒙)在𝒙𝟎处取得极大值𝒇(𝒙𝟎 )。 (2)如果在𝒙𝟎的左侧近旁,𝒇′(𝒙) < 𝟎,在𝒙𝟎的右侧近旁,𝒇′(𝒙) > 𝟎, 则函数𝒇(𝒙)在𝒙𝟎处取得极小值𝒇(𝒙𝟎 )。 (3)如果在𝒙𝟎的左右两侧近旁,𝒇′(𝒙)同号,𝒇(𝒙)在𝒙𝟎处没有极值