中国人民大学：《金融计量学》课程教学资源（PPT课件）Lecture 05 平稳金融时间序列——ARMA模型（1/2）

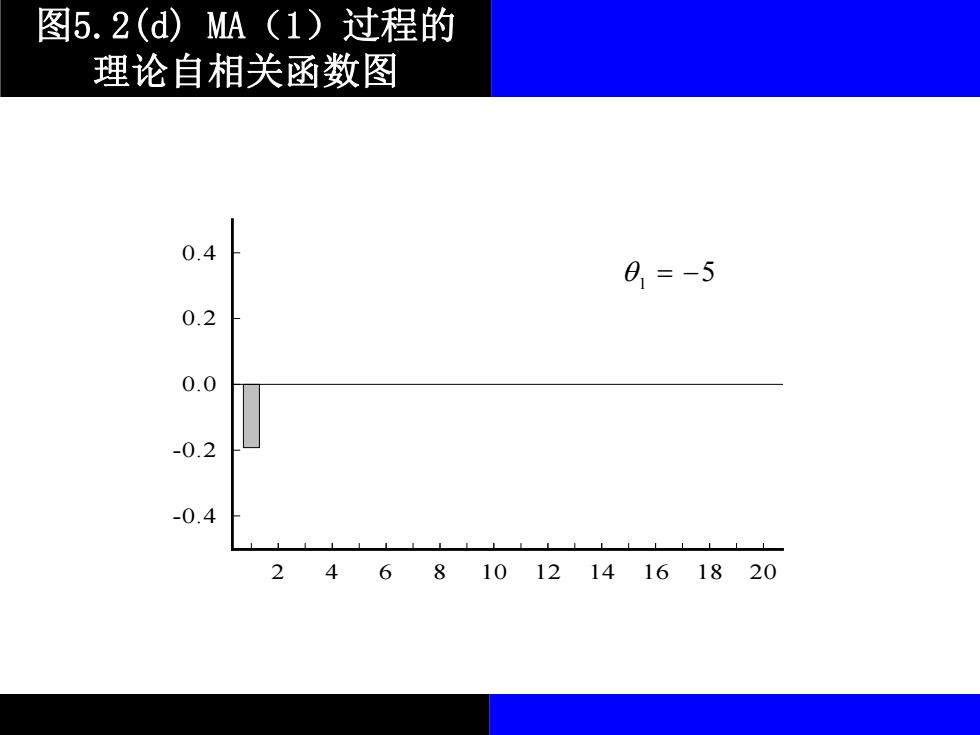
图5.2(d)MA(1)过程的 理论自相关函数图 0.4 0,=-5 0.2 0.0 -0.2 -0.4 2468101214161820

图5.2(d) MA（1）过程的 理论自相关函数图 -0.4 -0.2 0.0 0.2 0.4 2 4 6 8 10 12 14 16 18 20 1   5

可逆性(Invertibility) 对于9，<1， (1+0L)=1-0L+G2-G3L2+L (1+0L)1(y,-c)=8, (1-0,L+0L2-0L3+L)y,-c)=6

可逆性(Invertibility) 1 2 2 3 3 1 1 1 1 (1  L) 1  L  L  L       L 1 1 (1 ) ( ) L t t  y c      2 2 3 3 1 1 1 (1 )( ) L L L t t    L y  c   1 对于   1

对(1-0，L+02L2-0L3+L)y,-c)=6, 进行整理，不难看出其是一种无穷AR过 程，或写成AR(o),即： y.=(c-0c+gc-0c+L)+0y-0y2+L 以上推导过程说明了一个MA(1)过 程的可逆条件，即当0<1时，MA(1) 过程可逆。在这种情况下，MA(1)过 程可以“逆”过来写成的形式

对 进行整理,不难看出其是一种无穷AR过 程,或写成 , 即: 以上推导过程说明了一个MA(1)过 程的可逆条件，即当 时，MA(1) 过程可逆。在这种情况下， MA(1)过 程可以“逆”过来写成 的形式。 2 2 3 3 1 1 1 (1 )( ) L L L t t        L y  c   AR() 2 3 2 1 1 1 1 1 1 2 ( ) t t t y c  c  c  c  y  y     L     L 1   1

5.1.2MA(2)模型 y,=C+8,+8,8-1+828-2 均值 u=E(y,)=c 方差 Y=E(y-4)2=E(c,+06-1+08,-2)2 =(1+02+09)o1

5.1.2 MA(2) 模型 t t 1 t 1 2 t 2 y c            2 2 0 1 1 2 2 2 2 2 1 2 ( ) ( ) ( ) (1 ) t t t t t E y c E y E                        均值 方差

0,(1+02)02 j=1 Y1=0202 j=2 0 j>2 01(1+02) 1+82+0 ,j=1 02 1+02+0 ,j=2 。j>2

2 1 2 2 2 1 2 2 2 1 2 2 2 2 1 2 (1 ) , 1 , 2 0 , 2 (1 ) , 1 1 , 2 10 , 2 jj jjjjjj                                    