
机械与电气工程学院 School of Machanical and Elcetrical Engineering 二、动态特性 测试系统的动态特性是指当输入量(被测量)随时间变化时,输出量 (测量值)对输入的动态响应特性。 测试系统动态特性的优劣,关系到其输出随时间变化的规律(变化 曲线)是否能同时再现输入随时间变化的规律(变化曲线),即具有相同 的时间函数。 工程实际中除了少数的系统(如比例环节)外,输出信号与输入信号 之间具有不完全相同的时间函数,两者的差异就是所谓的动态误差。 机越与电气工程学院
机械与电气工程学院 School of Machanical and Elcetrical Engineering 二、动态特性 测试系统的动态特性是指当输入量(被测量)随时间变化时,输出量 (测量值)对输入的动态响应特性。 测试系统动态特性的优劣,关系到其输出随时间变化的规律(变化 曲线)是否能同时再现输入随时间变化的规律(变化曲线),即具有相同 的时间函数。 工程实际中除了少数的系统(如比例环节)外,输出信号与输入信号 之间具有不完全相同的时间函数,两者的差异就是所谓的动态误差
SME 机械与电气工程学院 School of Machanical and Elcetrical Engineering (一)问题的提出 一个随时间变化的力f(t)作用于质量弹簧k系统,求质心的位移。 解:设质心位移为y,弹簧的初始位移为yo, 系统的运动微分方程可表示为: m9+ko+ye1=mg+f回 因为 kyo =mg 所以 d2y(t) 77777777777777 m dt2 +ky(t)=f(t) 结论:系统的动态特性可由时域运动微分方程描述 机城与电气工程学院
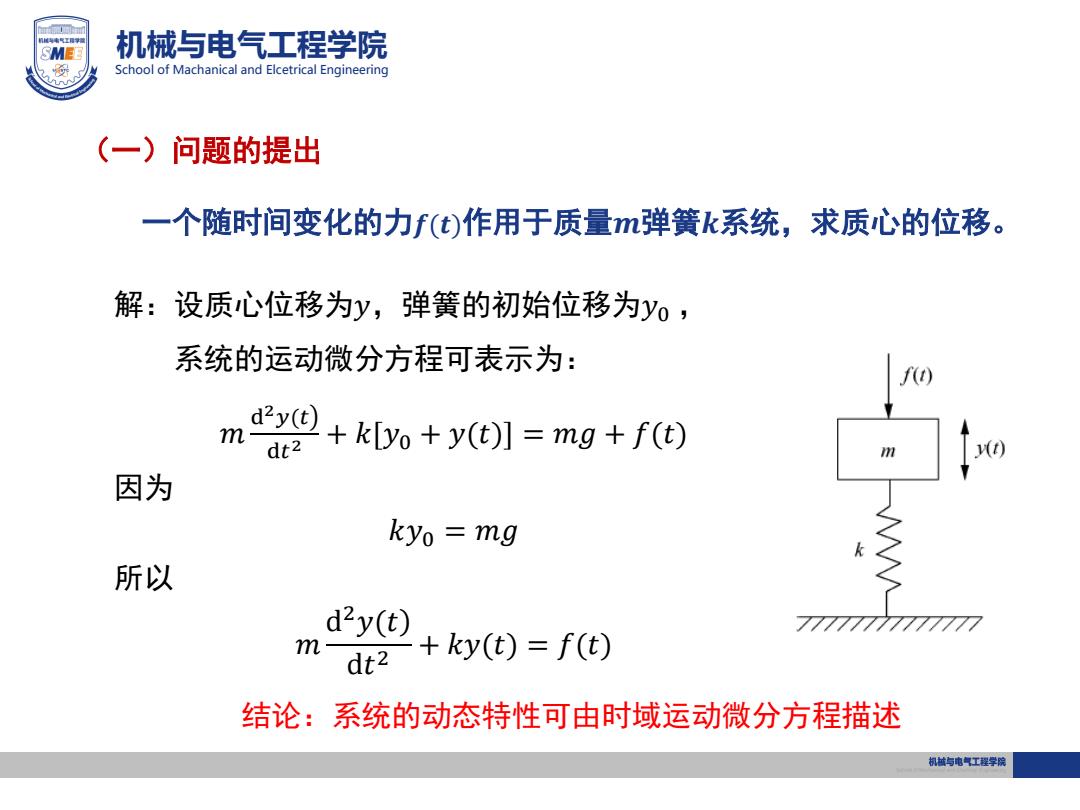
机械与电气工程学院 School of Machanical and Elcetrical Engineering 解:设质心位移为𝑦,弹簧的初始位移为𝑦0 , 系统的运动微分方程可表示为: 𝑚 d 2𝑦(𝑡 d𝑡 2 + 𝑘[𝑦0 + 𝑦(𝑡)] = 𝑚𝑔 + 𝑓(𝑡) 因为 𝑘𝑦0 = 𝑚𝑔 所以 𝑚 d ) 2𝑦(𝑡 d𝑡 2 + 𝑘𝑦(𝑡) = 𝑓(𝑡) 结论:系统的动态特性可由时域运动微分方程描述 (一)问题的提出 一个随时间变化的力𝒇(𝒕)作用于质量𝒎弹簧𝒌系统,求质心的位移

SMEE 机械与电气工程学院 School of Machanical and Elcetrical Engineering 以上系统是一个低阶系统,求解该运动微分方程并不困难。但 工程上大量存在的是复杂系统,其运动微分方程求解是很困难的, 有时甚至是不可能的。 因此在机械工程领域,通常采用一些足以反映系统的动态特性 的函数,把系统输入、输出联系到一起研究。 系统传递函数H(s) 频率响应函数HUω) 单位冲激函数h(t)
机械与电气工程学院 School of Machanical and Elcetrical Engineering 以上系统是一个低阶系统,求解该运动微分方程并不困难。但 工程上大量存在的是复杂系统,其运动微分方程求解是很困难的, 有时甚至是不可能的。 因此在机械工程领域,通常采用一些足以反映系统的动态特性 的函数,把系统输入、输出联系到一起研究。 系统传递函数𝐻(s) 频率响应函数𝐻(j𝜔) 单位冲激函数ℎ(t)