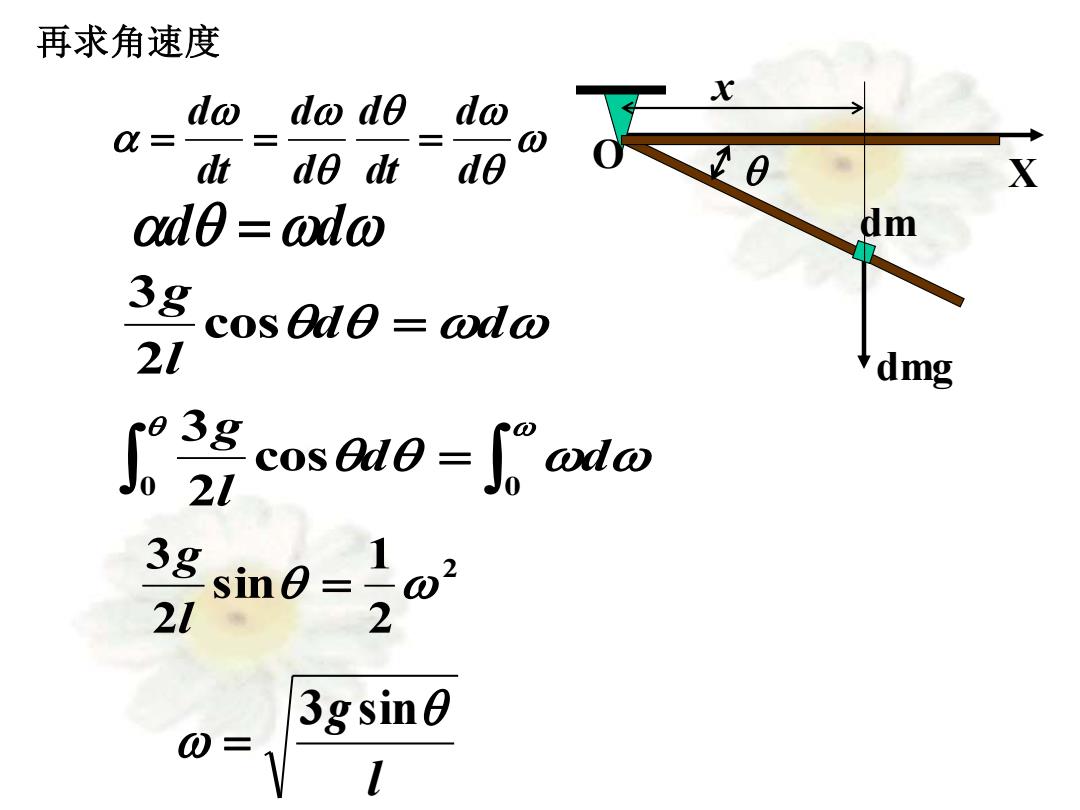
再求角速度 do dw do do Q= dt d0 dt X ad0 adw d m 3g cos ede=axda 21 dmg osaro- 3gsin0=201 21 2 3gsin 0=
dd dt d dd dt d = = = d d lg cos = 23 = 0 0 cos 23 d d lg 2 21 sin 23 = lg l g 3 sin = d = d 再求角速度 X O dmg dm x
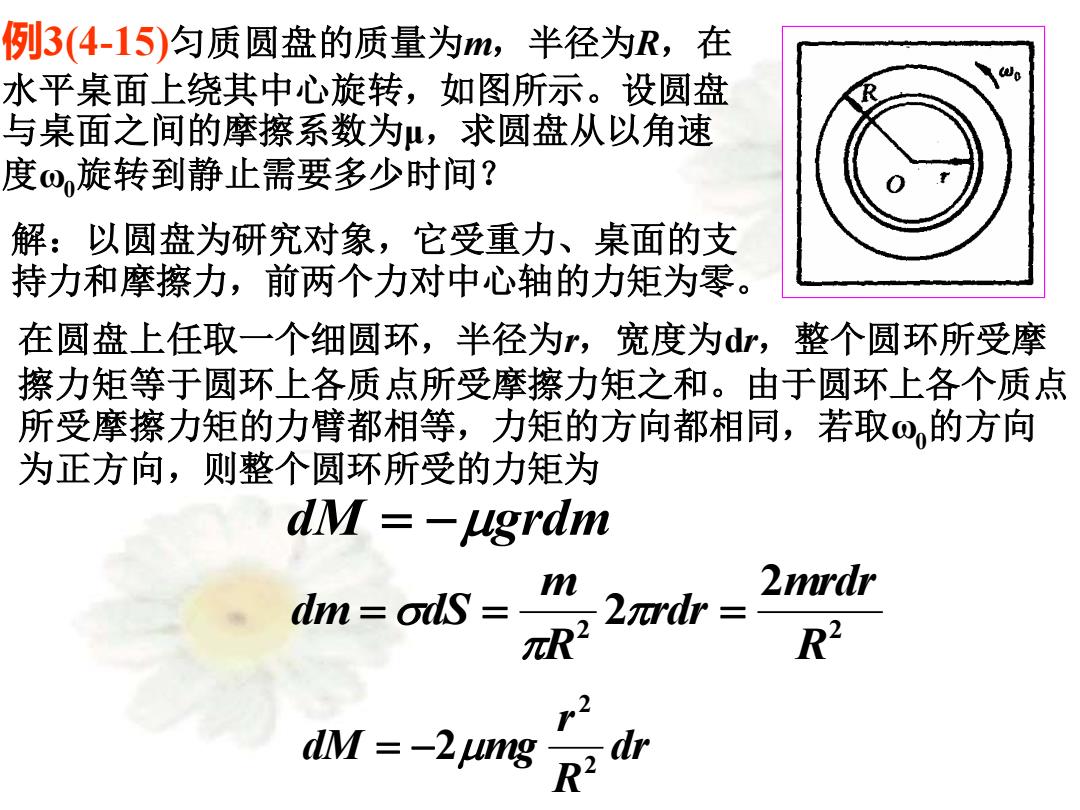
例3(4-15)匀质圆盘的质量为m,半径为R,在 水平桌面上绕其中心旋转,如图所示。设圆盘 与桌面之间的摩擦系数为μ,求圆盘从以角速 度o,旋转到静止需要多少时间? 解:以圆盘为研究对象,它受重力、桌面的支 持力和摩擦力,前两个力对中心轴的力矩为零。 在圆盘上任取一个细圆环,半径为r,宽度为,整个圆环所受摩 擦力矩等于圆环上各质点所受摩擦力矩之和。由于圆环上各个质点 所受摩擦力矩的力臂都相等,力矩的方向都相同,若取Q,的方向 为正方向,则整个圆环所受的力矩为 dM =-ugrdm n 2mrdr dm ods R2 2ardr R2 六2 dM =-2umg
例3(4-15)匀质圆盘的质量为m,半径为R,在 水平桌面上绕其中心旋转,如图所示。设圆盘 与桌面之间的摩擦系数为μ,求圆盘从以角速 度ω0旋转到静止需要多少时间? 解:以圆盘为研究对象,它受重力、桌面的支 持力和摩擦力,前两个力对中心轴的力矩为零。 在圆盘上任取一个细圆环,半径为r,宽度为dr,整个圆环所受摩 擦力矩等于圆环上各质点所受摩擦力矩之和。由于圆环上各个质点 所受摩擦力矩的力臂都相等,力矩的方向都相同,若取ω0的方向 为正方向,则整个圆环所受的力矩为 dM = −grdm2 2 2 2 R mrdr rdr R m dm = dS = = dr R r dM mg 2 2 = −2

整个圆盘所受的力矩为 R 2 M=∫-2gd=- 0 根据转动定律,得 2 M MmgR 48 a 3 mR2 3R 2 角加速度为常量,且与Q,的方向相反,表明圆盘作匀减速转动 0=00+0t 当圆盘停止转动时,0=0,则得 3R00 a Aug
整个圆盘所受的力矩为 dr mgR R r M mg R 3 2 2 0 2 2 = − = − 根据转动定律,得 R g mR mgR J M 3 4 2 1 3 2 2 = − − = = 角加速度为常量,且与ω0的方向相反,表明圆盘作匀减速转动 = +t 0 当圆盘停止转动时,ω=0,则得 g R t 4 0 3 0 = − =