
海大理学院赦学课件 大学物理学电子教案 刚体力学习题课
大学物理学电子教案 海大理学院教学课件 刚体力学习题课

1.对应 线量 角量 位置矢量 角位置 位 移 △产 角位移 △0 dr de 速 度 节= dt 角速度 dt dy d'r do d20 加速度 Q= 角加速度 a= dt dt2 dt dr2 =Vo at 0=0o+d S-So=Vot+ 2 8-0。=m,t+ 2 v2-vi=2a(s-so) o2-0=2a(0-0) 质 量 m 转动惯量 J 力 示 力 矩 M 牛顿定律 F=ma M=Ja 转动定律 动 能 1 Jω2 2 mv2 转动动能 2
1. 对应线 量 位置矢量 位 移 速 度 加 速 度 2 2 dt d r dt dv a dt dr v r r = = = 角 位 置 角 位 移 角 速 度 角加速度 2 2 dt d dt d dt d = = = 2 ( ) 2 1 0 2 0 2 2 0 0 0 v v a s s s s v t at v v at − = − − = + = + 2 ( ) 2 1 0 2 0 2 2 0 0 0 − = − − = + = + t t t 质 量 力 牛顿定律 动 能 2 2 1 mv F ma F m = 转动惯量 力 矩 转动定律 转动动能 2 2 1 J M J M J = 角 量
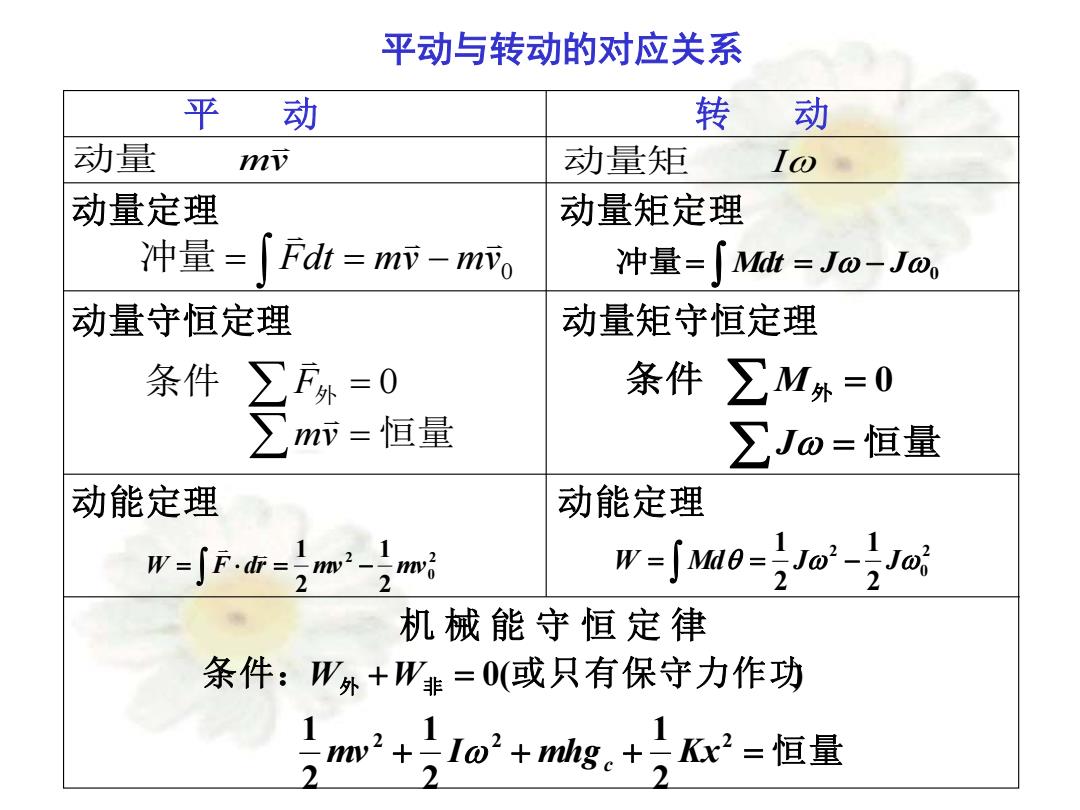
平动与转动的对应关系 平动 转动 动量 mv 动量矩 Io 动量定理 动量矩定理 冲量=「Fdt=mv-mv。 冲量=∫Mh=Jo-Jo, 动量守恒定理 动量矩守恒定理 条件 ∑F外=0 条件 ∑M外=0 ∑mm=恒量 ∑Jm=恒量 动能定理 动能定理 w-fFdr-m-mi 机械能守恒定律 条件:W外+W非=0(或只有保守力作功 2+w+脑g+号=恒量
平动与转动的对应关系 平 动 mv 动量 动量定理 0 Fdt mv mv = = − 冲量 动量守恒定理 = = 恒量 条件 外 J M 0 动能定理 2 0 2 2 1 2 1 W = F dr = mv − mv 机 械 能 守 恒 定 律 恒 量 条件: 外 非 或只有保守力作功 + + + = + = 2 2 2 2 1 2 1 2 1 0( ) mv I mhg Kx W W c 转 动 动量矩 I 动量矩定理 冲量= Mdt = J − J0 动量矩守恒定理 = = 恒量 条件 外 mv F 0 动能定理 2 0 2 2 1 2 1 W = Md = J − J

◆基本概念 转动惯量J.=∑△m 角动量L=J0 动力学特点 ◆刚体 转动定 M外z=Jz0 定轴转 律 动的特 点 外力矩所做的总功 W外a∫M6外d0 功能 特 转动动能定 m2=)Jo,2-a 理 重力势能:E。=mgh。转动动 Ek=Jo? 2 能 ◆其它规律与普通的质点系一样
= ⊥ i z i i J m r 转动惯量 2 基本概念 其它规律与普通的质点系一样 刚体 定轴转 动的特 点 W M d 外力矩所做的总功 外总 = 合外 转动动能定 理 2 1 2 12 2 2 1 2 1 W = J − J 重力势能: Ep = mghc 转动动 能 2 2 1 Ek = J 功能 特点 转动定 M外z = Jz 律 动力学特点 角动量 L z = Jz

1、有两个力作用在一个有固定轴的刚体上 (1)这两个力都平行于轴作用时,它们对轴的合力矩一定为0。 (2)这两个力都垂直于轴作用时,它们对轴的合力矩可能是0。 (3)当这两个力的合力为0时,它们对轴的合力矩也一定为0。 (4)当这两个力对轴的合力矩为0时,它们的合力也一定是0。 答:(1)、(2):正确 (3)、(4):不正确
1、有两个力作用在一个有固定轴的刚体上 (1) 这两个力都平行于轴作用时,它们对轴的合力矩一定为 0。 (2) 这两个力都垂直于轴作用时,它们对轴的合力矩可能是0。 (3) 当这两个力的合力为 0 时,它们对轴的合力矩也一定为 0。 (4) 当这两个力对轴的合力矩为 0 时,它们的合力也一定是 0。 答:(1)、(2): 正确 (3)、(4): 不正确