
在模糊集合的表达中,符号“/”、“+”和“∫”不 代表数学意义上的除号、加号和积分,它们是模糊集合的 一种表示方式,表示“构成”或“属于”。 模糊集合是以隶属函数来描述的,隶属度的概念是 模糊集合理论的基石。 例3.2设论域U={张三,李四,王五},评语为“学习好 ”。设三个人学习成绩总评分是张三得95分,李四得90 分,王五得85分,三人都学习好,但又有差异。 若采用普通集合的观点,选取特征函数 学习好∈A 学习差∈A
在模糊集合的表达中,符号“/” 、 “+”和“∫”不 代表数学意义上的除号、加号和积分,它们是模糊集合的 一种表示方式,表示“构成”或“属于” 。 模糊集合是以隶属函数来描述的,隶属度的概念是 模糊集合理论的基石。 例3.2 设论域U={张三,李四,王五},评语为“学习好 ” 。设三个人学习成绩总评分是张三得95分,李四得90 分,王五得85分,三人都学习好,但又有差异。 若采用普通集合的观点,选取特征函数 1 ( ) 0 A A C u A 学习好 学习差

此时特征函数分别为(张三)=1,(李四)=1,(王五)=1。 这样就反映不出三者的差异。假若采用模糊子集的概念,选 取[0,1]区间上的隶属度来表示它们属于“学习好”模糊子 集A的程度,就能够反映出三人的差异。 采用隶属函数4,(x)=x/100,由三人的成绩可知三 人“学习好”的隶属度为(张三)=0.95,(李四)=0.90,(王 五)=0.85。用“学习好”这一模糊子集A可表示为: A=095.0900.85 其含义为张三、李四、王五属于“学习好”的程度 分别是0.95,0.90,0.85
此时特征函数分别为(张三)=1,(李四)=1,(王五)=1。 这样就反映不出三者的差异。假若采用模糊子集的概念,选 取[0,1]区间上的隶属度来表示它们属于“学习好”模糊子 集A的程度,就能够反映出三人的差异。 采用隶属函数 ,由三人的成绩可知三 人“学习好”的隶属度为(张三)=0.95,(李四)=0.90,(王 五)=0.85。用“学习好”这一模糊子集A可表示为: ( ) /100 A x x A{0.95,0.90,0.85} 其含义为张三、李四、王五属于“学习好”的程度 分别是0.95,0.90,0.85

例3.3以年龄为论域,取X=[02o。Zadeh:给出了“年轻” 的模糊集Y,其隶属函数为 0≤x≤25 25<x≤100 通过Matlab仿真对上述隶属函数作图,隶属函数曲线 如图所示
X 0,200 1 2 0 0 25 ( ) 25 1 25 100 5 x Y x x x
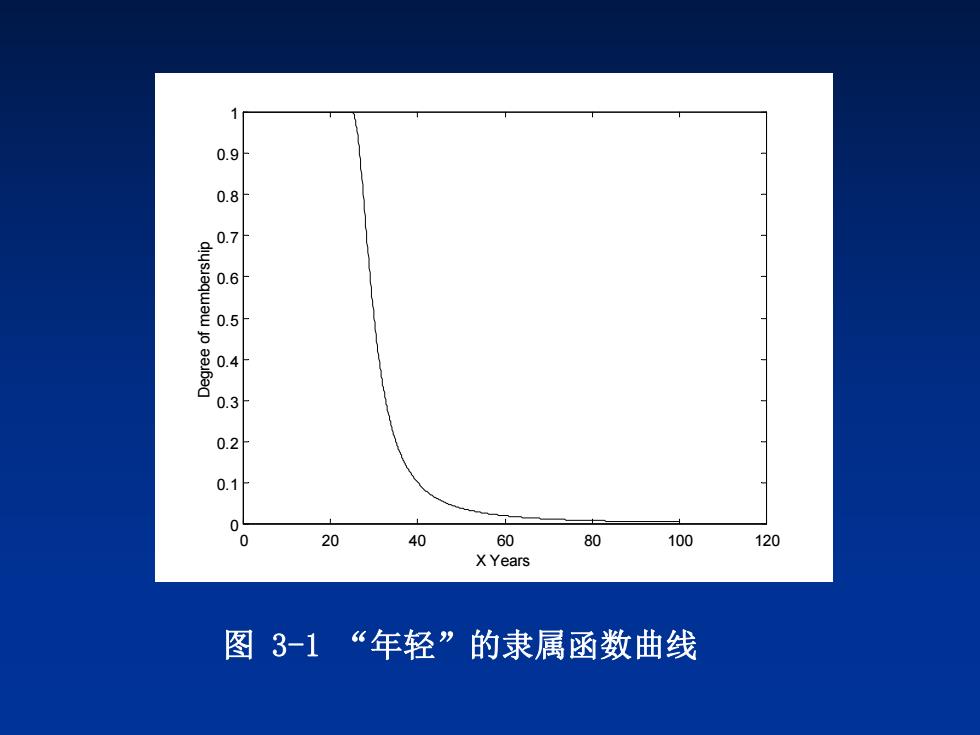
0.9 0.8 01 06 0 0.4 0.3 0.2 0.1 0 20 40 60 80 100 120 X Years 图3-1“年轻”的隶属函数曲线
0 20 40 60 80 100 120 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 X Years D e gre e of m e m b ers hip 图 3-1 “年轻”的隶属函数曲线

二、模糊集合的运算 1模糊集合的基本运算 由于模糊集是用隶书函数来表征的,因此两个子集之 间的运算实际上就是逐点对隶属度作相应的运算。 (1)空集 模糊集合的空集为普通集,它的隶属度为0,即 4=中台L(0)=0 (2)全集 模糊集合的全集为普通集,它的隶属度为1,即 A=E台u4()=1
A A (u) 0 (2)全集 模糊集合的全集为普通集,它的隶属度为1,即 A E A(u) 1