
1产品组合模型 1.1引言 从理论上说,产品组合问题是最容易理解的最优化问题。Astro/Cosmo问题就是早期的一 个例子。虽然在简单教科书中介绍的产品组合问题很少在实践中遇到,但是他们常常是一些 大问题的重要组成部分,如多期计划模型。 产品组合问题的特征是:产品的生产要消耗有限的资源。如果有m种资源和n个产品,那 么我们可以用一张m行、n列的表格来表示生产的技术水平。在第i行、第j列格子中的数字就 是每个单位产品消耗资源的数量。表格一行中的系数就是LP问题中一个约束的系数。在简 单的产品组合问题中,这些系数都是非负的。此外,我们还给出每种产品的单件利润和每种 可用资源的数量。最优化的目的就是要确定在不超过现有资源的限制条件下,每种产品生产 多少(组合就是此意),才可以获得最大的利润。 下面将要介绍的例子不只是用来说明如何求解产品组合问题的LP模型,而且还将说明(1) 如何处理非线性利润函数(2)对于大多数的最优化问题都有可替代的正确的处理方法。就是 说,人们对同样的一个问题可以采用两种不同的方法去处理,但结果都是正确的。 1.2典型案例 某一工厂能够制造出五种不同的产品。每种产品所需机器的时间见下表(分/单位): Machine(机器) Product(产品) 1 2 3 A 12 5 B 7 9 10 c 8 4 7 D 10 0 3 E > 11 ) 每部机器每星期可提供128个工作小时
1 产品组合模型 1.1 引言 从理论上说,产品组合问题是最容易理解的最优化问题。Astro/Cosmo问题就是早期的一 个例子。虽然在简单教科书中介绍的产品组合问题很少在实践中遇到,但是他们常常是一些 大问题的重要组成部分,如多期计划模型。 产品组合问题的特征是:产品的生产要消耗有限的资源。如果有m种资源和n个产品,那 么我们可以用一张m行、n列的表格来表示生产的技术水平。在第i行、第j列格子中的数字就 是每个单位产品j消耗资源i的数量。表格一行中的系数就是LP问题中一个约束的系数。在简 单的产品组合问题中,这些系数都是非负的。此外,我们还给出每种产品的单件利润和每种 可用资源的数量。最优化的目的就是要确定在不超过现有资源的限制条件下,每种产品生产 多少(组合就是此意),才可以获得最大的利润。 下面将要介绍的例子不只是用来说明如何求解产品组合问题的LP模型,而且还将说明(1) 如何处理非线性利润函数(2)对于大多数的最优化问题都有可替代的正确的处理方法。就是 说,人们对同样的一个问题可以采用两种不同的方法去处理,但结果都是正确的。 1.2 典型案例 某一工厂能够制造出五种不同的产品。每种产品所需机器的时间见下表(分/单位): Machine(机器) Product(产品) 1 2 3 A 12 8 5 B 7 9 10 C 8 4 7 D 10 0 3 E 7 11 2 每部机器每星期可提供128个工作小时

产品A,B和C自由竞争,而且数量不限,并每个能分别卖$5,$4和$5。每一星期,D和E 的最初20个产品每个可卖$4,但是超过的部分每个只能卖$3。对于机器1和2,每小时的劳动 费用分别为$4:而对于机器3,每小时的劳动费用为$3。产品A和C的材料费都是$2:而产品 B,D和E的材料费都是$1。你目标就是使公司能够获得最大利润。 首要的困难是产品D和E的利润是非线性的。为了解决这一困难,你可以采取下面的策略。 定义两个附加的产品D2和E2,每单位产品卖$3。他们的上限也一定受制于原始的产品D和E 的限制。决策变量和他们贡献的利润如下: 每一单位产品 决策变量 定义 贡献的利润 A 每一星期产品A的数量 5-2=$3 B 每一星期产品B的数量 4-1=$3 C 每一星期产品C的数量 5-2=$3 D 每一星期产品D的数量(20个以内) $3 D2 每一星期产品D的数量(超过20个的部分)* $2 每一星期单位产品E的数量(20个以内)》 $3 E2 每一星期单位产品E的数量(超过20个的部分) $2 M 每一星期使用机器1的小时数 -$4 M 每一星期使用机器2的小时数 -$4 M 每一星期使用机器3的小时数 -$3 *产品D的总数是D+D2。 我们不必考虑不同产品在每一部机器上加工的先后顺序问题。如果产品的交货时间足够 长,这种假设是合理的。在这种情况下,我们的问题是: Maximize 收入减去成本 Subject to 产品在每部机器上使用的时间等于机器运行的时间, 产品D和E的产量最多不能超过20个, 每部机器最多可使用128个小时。 下面用LINGO更精确、更明确地描述如下: !最大化收入减去成本: MAX=3*A+3*B+3*C+3*:D+2*D2+3*E+2*:E2 -4*M1-4*M2-3*M3:
产品A,B和C自由竞争,而且数量不限,并每个能分别卖$5,$4和$5。每一星期,D和E 的最初20个产品每个可卖$4,但是超过的部分每个只能卖$3。对于机器1和2,每小时的劳动 费用分别为$4;而对于机器3,每小时的劳动费用为$3。产品A和C的材料费都是$2;而产品 B,D和E的材料费都是$1。你目标就是使公司能够获得最大利润。 首要的困难是产品D和E的利润是非线性的。为了解决这一困难,你可以采取下面的策略。 定义两个附加的产品D2和E2,每单位产品卖$3。他们的上限也一定受制于原始的产品D和E 的限制。决策变量和他们贡献的利润如下: 每一单位产品 决策变量 定义 贡献的利润 A 每一星期产品A的数量 5 - 2 = $3 B 每一星期产品B的数量 4 - 1 = $3 C 每一星期产品C的数量 5 - 2 = $3 D 每一星期产品D的数量(20个以内) $3 D2 每一星期产品D的数量(超过20个的部分)* $2 E 每一星期单位产品E的数量(20个以内) $3 E2 每一星期单位产品E的数量(超过20个的部分) $2 M1 每一星期使用机器1的小时数 -$4 M2 每一星期使用机器2的小时数 -$4 M3 每一星期使用机器3的小时数 -$3 *产品D的总数是D+D2。 我们不必考虑不同产品在每一部机器上加工的先后顺序问题。如果产品的交货时间足够 长,这种假设是合理的。在这种情况下,我们的问题是: Maximize 收入减去成本 Subject to 产品在每部机器上使用的时间等于机器运行的时间, 产品D和E的产量最多不能超过20个, 每部机器最多可使用128个小时。 下面用LINGO更精确、更明确地描述如下: ! 最大化 收入减去成本; MAX = 3 * A + 3 * B + 3 * C + 3 * D + 2 * D2 + 3 * E + 2 * E2 - 4 * M1 - 4 * M2 - 3 * M3;
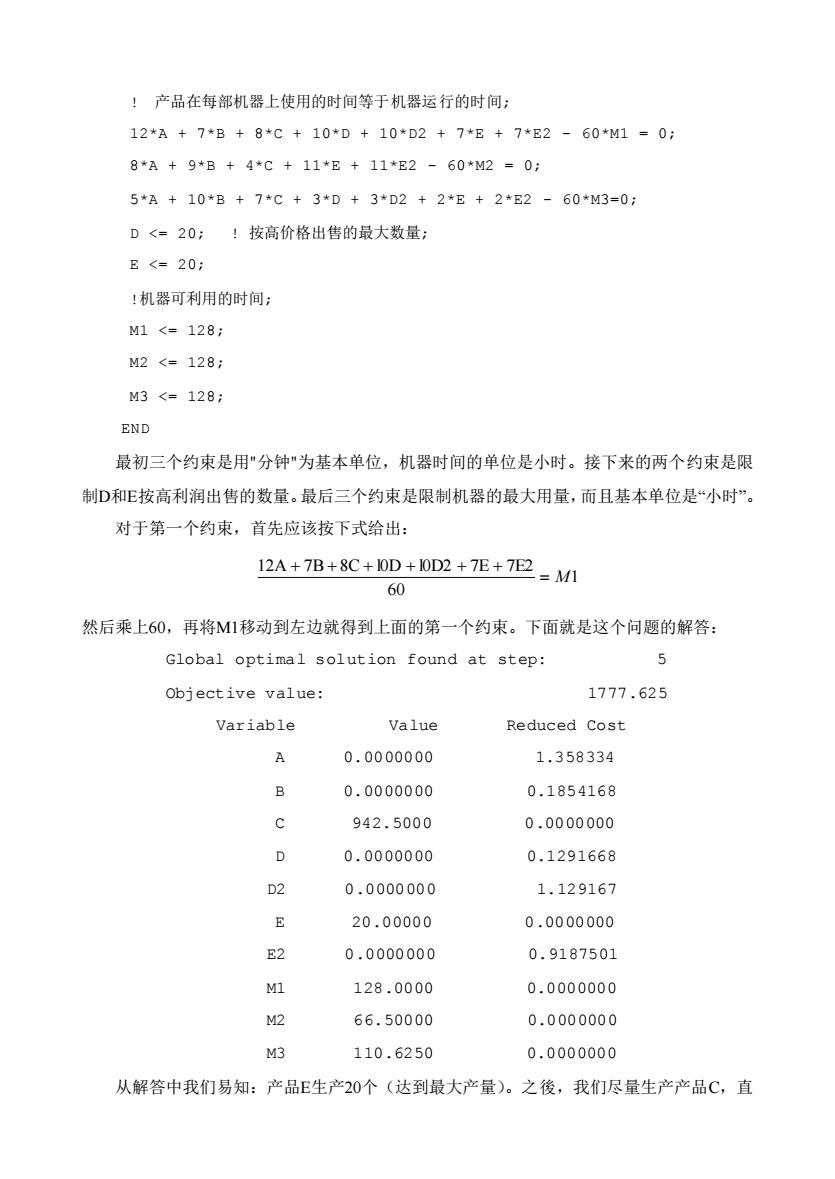
!产品在每部机器上使用的时间等于机器运行的时间: 12*A+7*B+8*C+10*D+10*D2+7*E+7*E2-60*M1=0: 8*A+9*B+4*C+11*E+11*E2-60*M2=0; 5*A+10*B+7*C+3*D+3*D2+2*E+2*E2-60*M3=0; D<=20: !按高价格出售的最大数量: E<=20: !机器可利用的时间: M1<=128: M2<=128: M3<=128; END 最初三个约束是用"分钟“为基本单位,机器时间的单位是小时。接下来的两个约束是限 制D和E按高利润出售的数量。最后三个约束是限制机器的最大用量,而且基本单位是“小时”。 对于第一个约束,首先应该按下式给出: 12A+7B+8C+10D+0D2+7E+72=M1 60 然后乘上60,再将M1移动到左边就得到上面的第一个约束。下面就是这个问题的解答: Global optimal solution found at step: 5 Obiective value: 1777.625 Variable Value Reduced Cost A 0.0000000 1.358334 B 0.0000000 0.1854168 c 942.5000 0.0000000 0 0.0000000 0.1291668 D2 0.0000000 1.129167 E 20.00000 0.0000000 E2 0.0000000 0.9187501 Ml 128.0000 0.0000000 M2 66.50000 0.0000000 M3 110.6250 0.0000000 从解答中我们易知:产品E生产20个(达到最大产量)。之後,我们尽量生产产品C,直
! 产品在每部机器上使用的时间等于机器运行的时间; 12*A + 7*B + 8*C + 10*D + 10*D2 + 7*E + 7*E2 - 60*M1 = 0; 8*A + 9*B + 4*C + 11*E + 11*E2 - 60*M2 = 0; 5*A + 10*B + 7*C + 3*D + 3*D2 + 2*E + 2*E2 - 60*M3=0; D <= 20; ! 按高价格出售的最大数量; E <= 20; !机器可利用的时间; M1 <= 128; M2 <= 128; M3 <= 128; END 最初三个约束是用"分钟"为基本单位,机器时间的单位是小时。接下来的两个约束是限 制D和E按高利润出售的数量。最后三个约束是限制机器的最大用量,而且基本单位是“小时”。 对于第一个约束,首先应该按下式给出: 1 60 12A 7B 8C l0D l0D2 7E 7E2 = M + + + + + + 然后乘上60,再将M1移动到左边就得到上面的第一个约束。下面就是这个问题的解答: Global optimal solution found at step: 5 Objective value: 1777.625 Variable Value Reduced Cost A 0.0000000 1.358334 B 0.0000000 0.1854168 C 942.5000 0.0000000 D 0.0000000 0.1291668 D2 0.0000000 1.129167 E 20.00000 0.0000000 E2 0.0000000 0.9187501 M1 128.0000 0.0000000 M2 66.50000 0.0000000 M3 110.6250 0.0000000 从解答中我们易知:产品E生产20个(达到最大产量)。之後,我们尽量生产产品C,直

到达到机器1的最大承受能力。 对于这个例题,我们还可以非常容易地找到其它等价的解法。这些解法不仅正确而且还 具有较少的变量和约束。例如,对于约束 8A+9B+4C+11E+11E2-60M2=0 可以重写为 M2=(8A+9B+4C+11E+11E2)/60 在模型中任何位置出现的M2都可以用上式右边的表达式替换。因为右边的表达式总是非 负的。非负的约束将会自动地被满足。因此,如果我们做这样的数学替换,M2和上述的约束 都能从模型中除去。类似地,我们还可以对M1和M3作同样的处理。这样,我们就得到下面 的模型: Model: MAX=1.41667*A+1.4333*B+1.85*C+2.18334*D+1.1833*D2+1.7*E+0.7*E2; !产品在每部机器上使用的时间等于机器运行的时间; 12*A+7*B+8*C+10*D+10*D2+7*E+7*E2<=7680: 8*A+9*B+4*C+11*E+11*E2 <=7680; 5*A+10*B+7*C+3*D+3*D2 +2*E+2*E2<=7680: !产品限制: D<=20; E<=20; End 这看起来更象是一个标准的产品组合模型。所有的约束都属于同一个类型。注意:这个 模型的解答和前面模型的解答完全一样。 Global optimal solution found at step: 3 Objective value: 1777.625 Variable Va lue Reduced Cost A 0.0000000 1.358333 B 0.0000000 0.1854170 942.5000 0.0000000 D 0.0000000 0.1291660 D2 0.0000000 1.129167 E 20.00000 0.0000000
到达到机器1的最大承受能力。 对于这个例题,我们还可以非常容易地找到其它等价的解法。这些解法不仅正确而且还 具有较少的变量和约束。例如,对于约束 8A+9B+4C+ 11E+ llE2- 60M2 = 0 可以重写为 M2 = (8A + 9B + 4C + 11E + 11E2)/60 在模型中任何位置出现的M2都可以用上式右边的表达式替换。因为右边的表达式总是非 负的。非负的约束将会自动地被满足。因此,如果我们做这样的数学替换,M2和上述的约束 都能从模型中除去。类似地,我们还可以对M1和M3作同样的处理。这样,我们就得到下面 的模型: Model: MAX=1.41667*A+1.4333*B+1.85*C+2.18334*D+1.1833*D2+1.7*E+0.7*E2; ! 产品在每部机器上使用的时间等于机器运行的时间; 12*A + 7*B + 8*C + 10*D + 10*D2 + 7*E + 7*E2 <= 7680; 8*A + 9*B + 4*C + 11*E + 11*E2 <= 7680; 5*A + 10*B + 7*C + 3*D + 3*D2 + 2*E + 2*E2 <= 7680; ! 产品限制; D <= 20; E < =20; End 这看起来更象是一个标准的产品组合模型。所有的约束都属于同一个类型。注意:这个 模型的解答和前面模型的解答完全一样。 Global optimal solution found at step: 3 Objective value: 1777.625 Variable Value Reduced Cost A 0.0000000 1.358333 B 0.0000000 0.1854170 C 942.5000 0.0000000 D 0.0000000 0.1291660 D2 0.0000000 1.129167 E 20.00000 0.0000000

E2 0.0000000 0.9187500 对于不太善于数学的建模者来说,他可能会给出第一种模型。然而,对于喜欢数学的建 模者就可能给出第二个模型。 1.3案例及参考解答 1-1.假设某个公司生产Widgets和Frisbees两种产品。每一种产品都是两种原材料聚酯和 聚乙烯制成的。下面的表格就给出了产品消耗原材料的数据: Widgets Frisbees 原材料 3 聚酯 6 2 聚乙烯 由于进口的限制,这个月,公司只能分别得到12单位聚酯和10单位聚乙烯。公司对下个 月的生产计划非常感兴趣。为此,知道每一种产品的获利情况就变得非常重要。单位产品 Widgets7和Frisbees可分别获利S3和$4。下个月,Widgets和Frisbees应该生产多少? 参考解答: Model: !W和F分别表示Widgets和Frisbees两种产品的产量: 3*W+5*F<12: 6*N+2*F<10: max=3*W+4*F; End 解答: Objective value: 10.25000 Variable Value Reduced Cost W 1.083333 0.0000000 1.750000 0.0000000 总利润为10.25美元。 l-2.Otto Maddick机械制造公司生产两种产品:消声器轴承(muffler beating)和转力矩
E2 0.0000000 0.9187500 对于不太善于数学的建模者来说,他可能会给出第一种模型。然而,对于喜欢数学的建 模者就可能给出第二个模型。 1.3 案例及参考解答 1-1. 假设某个公司生产Widgets和Frisbees两种产品。每一种产品都是两种原材料聚酯和 聚乙烯制成的。下面的表格就给出了产品消耗原材料的数据: Widgets Frisbees 原材料 3 5 聚酯 6 2 聚乙烯 由于进口的限制,这个月,公司只能分别得到12单位聚酯和10单位聚乙烯。公司对下个 月的生产计划非常感兴趣。为此,知道每一种产品的获利情况就变得非常重要。单位产品 Widgets和Frisbees可分别获利$3和$4。下个月,Widgets和Frisbees应该生产多少? 参考解答: Model: !W和F分别表示Widgets和Frisbees两种产品的产量; 3*W+5*F<12; 6*W+2*F<10; max=3*W+4*F; End 解答: Objective value: 10.25000 Variable Value Reduced Cost W 1.083333 0.0000000 F 1.750000 0.0000000 总利润为10.25美元。 1-2. Otto Maddick机械制造公司生产两种产品:消声器轴承(muffler beating)和转力矩