
Lambertian Surface Appears equally bright from all viewing directions Reflects all light without absorbing Matte surface,no "shiny"spots Brightness of the surface as seen from camera is linearly correlated to the amount of light falling on the surface Here we will discuss only Lambertian surfaces under point-source illumination
Lambertian Surface ▪ Appears equally bright from all viewing directions ▪ Reflects all light without absorbing ▪ Matte surface, no “shiny” spots ▪ Brightness of the surface as seen from camera is linearly correlated to the amount of light falling on the surface Here we will discuss only n Lambertian surfaces under point-source illumination

Some Notations: Surface Orientation A smooth surface has a tangent plane at every point Mark p =7 z Oz ay ■ Parametrize surface orientation by first partial derivatives of z }q8y f pox (X,Y) y
Some Notations: Surface Orientation

Some Notations: Surface Orientation Surface normal 口x=(p,0,1),y=(0,q,1) ▣ n=rx×y=(p,q,-1) Normalize元=品 (p,q,-1) p2+q2+1 0 z 剂 p= 0x9= ay Fq8y pox (xY)
Some Notations: Surface Orientation

Reflectance Map Relationship between surface orientation and brightness Lambertian surface R(p,q)=in·1= 1+psp+qsq V1+p2+q2V1+ps2+9s2 Image irradiance(brightness)is proportional 湖 to R I(x,y)=R(p,q) 凝
Reflectance Map ▪
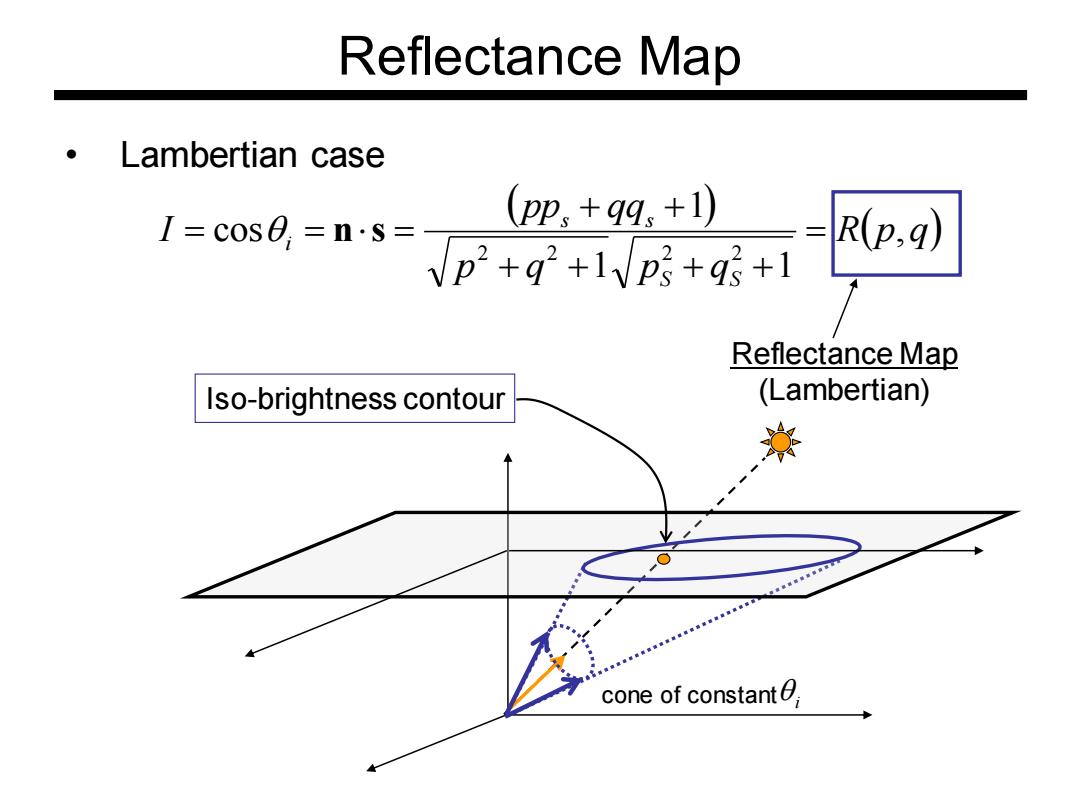
Reflectance Map Lambertian case I=c0s0,=n·s= (pp,+qq,+1 、==R(p,g Vp2+g2+1Vp&+g+1 Reflectance Map Iso-brightness contour (Lambertian) cone of constant
• Lambertian case ( ) R(p q) p q p q pp qq I S S s s i , 1 1 1 cos 2 2 2 2 = + + + + + + = = ns = Reflectance Map (Lambertian) cone of constant i Iso-brightness contour Reflectance Map