数字电子发术 第5章触发器 4.1 基本触发器 4.1.1由与非门组成 On+l S=R=1 一、电路及符号 61 保持 S=1,R=0 态 0n+1= & “置0”或“复位”(Reset) R R R 置1”或“置位”(Set) 号10态 2 1态 S=R=02和2均为U1 =0 R先撤消:→1态 二、工作原理 S先撤消:→0态 信号同时撤消:状态不定
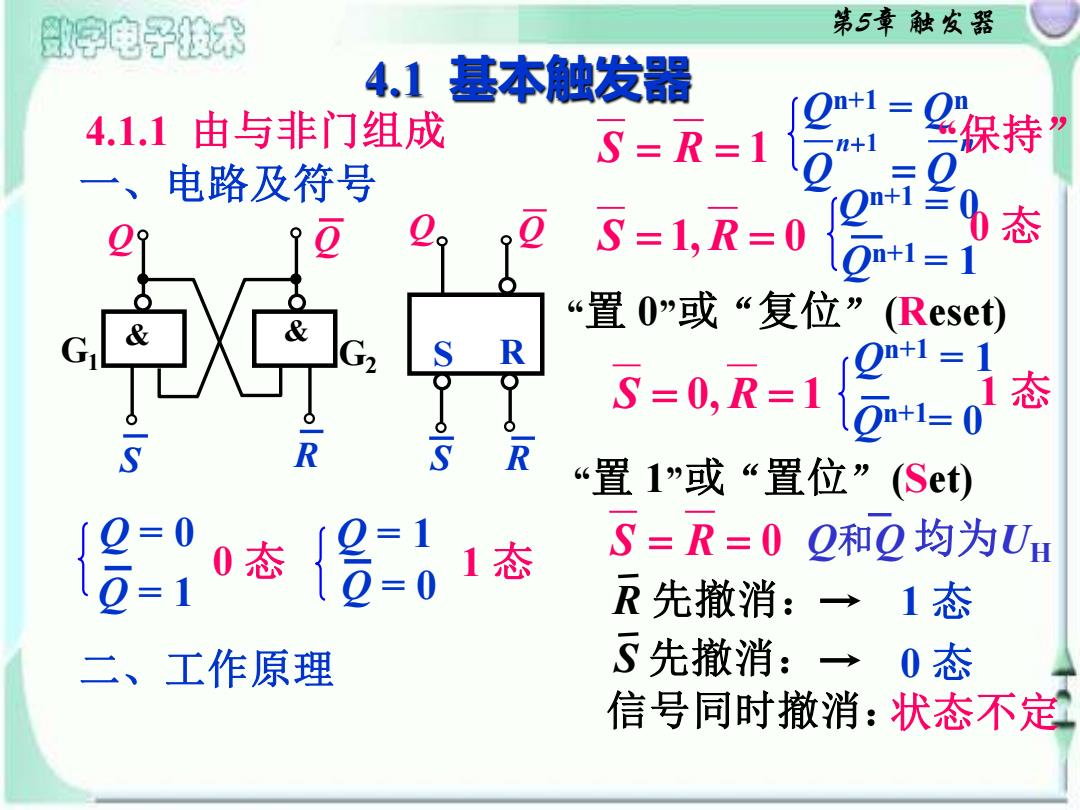
第5章 触发器 G2 4.1 基本触发器 4.1.1 由与非门组成 一、电路及符号 Q G1 R & & S Q Q Q S R S R Q = 0 Q = 1 0 态 Q = 1 Q = 0 1 态 二、工作原理 S = R = 1 Qn+1 = Qn n n 1 Q Q + = “保持” S = 1, R = 0 Qn+1 = 0 Qn+1 = 1 0 态 “置 0”或“复位”(Reset) S = 0, R = 1 Qn+1 = 1 Qn+1= 0 1 态 “置 1”或“置位”(Set) S = R = 0 Q和Q 均为UH R 先撤消: 1 态 S 先撤消: 0 态 信号同时撤消:状态不定
数字电子技述 三、特性表、特性方程和波形图 简化特性表 卡诺图 RS Q +1 +1 00 X 不用 00 0111 10 01 0 置0 10 1 置1 11 保持 0 Q1=S+R0” 特性方程: RS=0约束条件
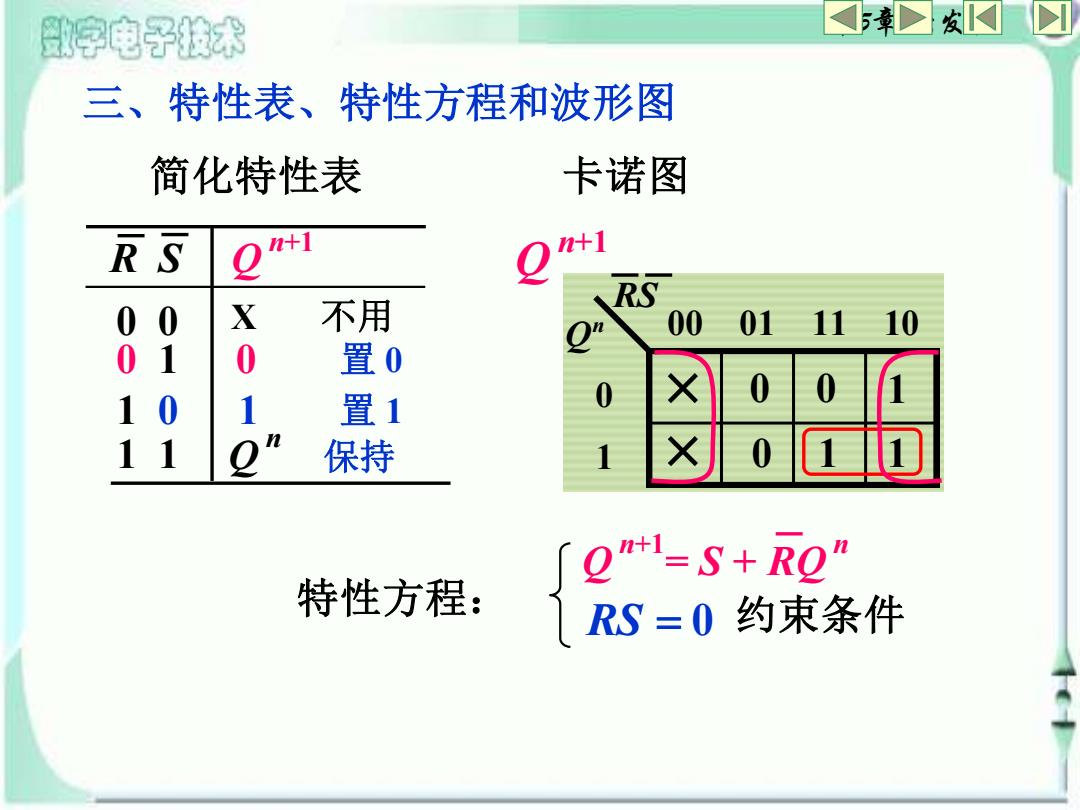
第5章 触发器 三、特性表、特性方程和波形图 简化特性表 R S Q n+1 0 0 0 1 1 0 1 1 Q n 保持 0 置 0 1 置 1 X 不用 卡诺图 RS 0 1 Q n 00 01 11 10 Q n+1 0 1 0 0 1 1 Q n+1 = S + RQ n 特性方程: RS = 0 约束条件

数字电子发术 课本上 表5.1.1特性表 表5.1.2简化特性表 RS +1 RS n+l 0 保持 0 0 0 0 1 置1 0 0 1 0 置0 0 1 0 1 11 不用 不允许 0 1 1 1 0 0 0 +1 1 0 1 0 RS 00 0111 10 1 0 不用 11 1 不用 Q1=S+R0” 0 特性方程 RS=0约束条件 图5.1.7卡诺图
第5章 触发器 课本上 表5.1.1 特性表 R S Qn Q n+1 0 0 0 0 0 1 0 1 0 0 1 1 1 0 0 1 0 1 1 1 0 1 1 1 0 1 1 1 0 0 不用 不用 R S Q n+1 0 0 0 1 1 0 1 1 Q n 保持 1 置 1 0 置 0 不用 不允许 图5.1.7 卡诺图 RS 0 1 Q n 00 01 11 10 Q n+1 0 1 1 1 0 0 Q n+1 = S + RQ n RS = 0 约束条件 表5.1.2 简化特性表 特性方程

工作波形图 它能具体反映触发器在置1和置0过 G1 G2 化间的时序关系。 当 当 S:1→0, R:1→0, R=1时 21pd 5=1时, 先于 Q 0先于Q 变化。 变化。 12 图4.1.4基本RS触发器翻转过程波形图
第5章 触发器 工作波形图 它能具体反映触发器在置1和置0过程中各信号变 化间的时序关系。 图4.1.4 基本RS触发器翻转过程波形图 当 S :1 0, R 1 → = Q 先于 Q 变化。 时, 当 R :1 0, S 1 → = Q 先于 Q 变化。 时, 1 t 2 t 3 t 4 t
数字电子技术 简化波形图 实际中信号的状态转换时间及门电 路的传输延迟时间都很短,相对于 脉冲的宽度和周期可视为0,得其 简化波形 设触发器初始状态为0: R S 一R 2 0 图4.1.5简化波形
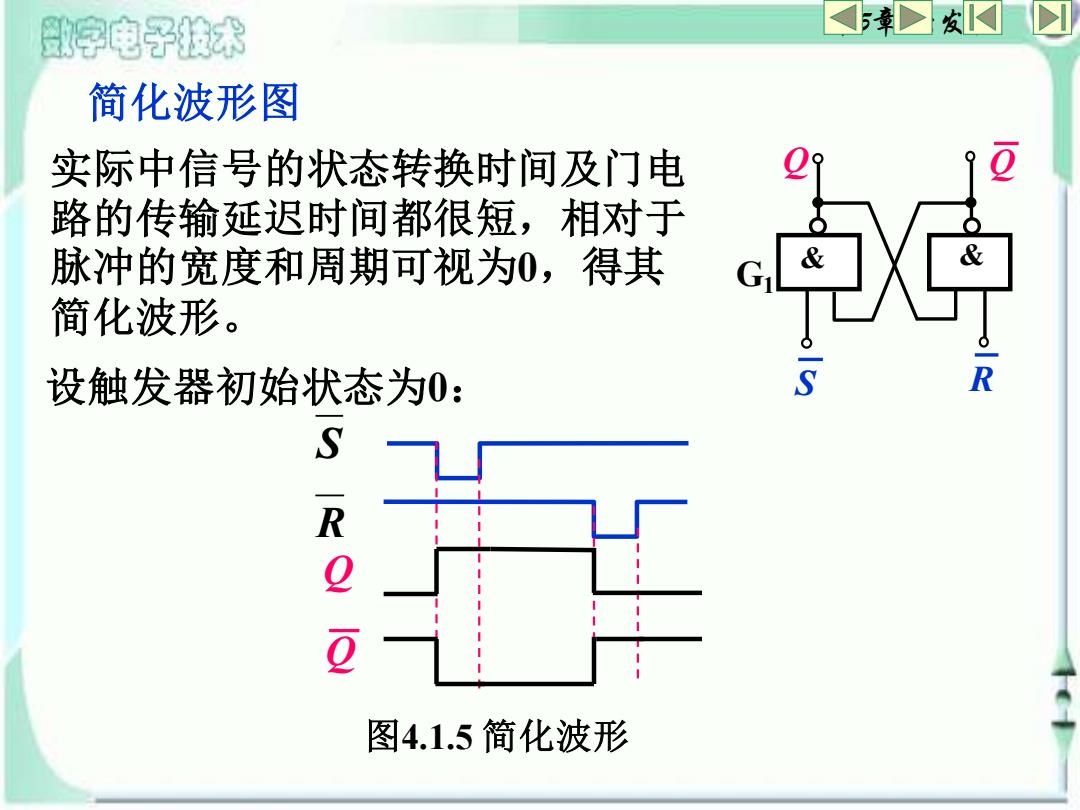
第5章 触发器 简化波形图 实际中信号的状态转换时间及门电 路的传输延迟时间都很短,相对于 脉冲的宽度和周期可视为0,得其 简化波形。 Q G1 R & & S Q 设触发器初始状态为0: S R Q Q 图4.1.5 简化波形