
据如下(单位:元),1500、750、780、1080、850、960、2000、1250、1630,计算人均月收入的四分位数。Q,的位置=叫1_91-2.5解:44,即QL在第2个数值(780)和第3个数值(850)之间0.5的位置上,因此QL=(780+850)2=815(元)3(n+1)_ 3×(9+1)Qu的位置=37.544,即QU在第7个数值(1500)和第8个数值(1630)之间0.5的位置上,因此QU=(1500+1630)-2=1565(元)QL和QU之间包含了50%的数据,因此,我们可以说有一半的家庭人均月收入在815~1565元之间。(2)组距分组数据:Q,位置=ZQ,位置_3Z44数值型分组数据的四分位数(计算公式)2f-S.4下四分位数:xilQL+J(0(3.10)3ZFSu4上四分位数Qu=Lu +xiufu(3.10)三、数值型数据集中趋势的测度(一)算术平均数算术平均数(Arithmeticmean)也称为均值(Mean),是全部数据算术平均的结果。算术平均法是计算平均指标最基本、最常用的方法。计算公式为:总体标志总量算术平均数=总体单位总量很多社会经济现象,总体标志总量常常是总体单位变量值的算术总和。例如
据如下(单位:元),1500、750、780、1080、850、960、2000、1250、1630,计 算人均月收入的四分位数。 解: L n+1 9+1 Q = =2.5 4 4 的位置= ,即 QL 在第 2 个数值(780)和第 3 个数值(850) 之间 0.5 的位置上,因此 QL=(780+850)÷2=815(元) U 3(n+1) 3 (9+1) Q = =7.5 4 4 的位置= ,即 QU 在第 7 个数值(1500)和第 8 个数值 (1630)之间 0.5 的位置上,因此 QU=(1500+1630)÷2=1565(元) QL 和 QU 之间包含了 50%的数据,因此,我们可以说有一半的家庭人均月收 入在 815~1565 元之间。 (2)组距分组数据: 4 = f QL位置 4 3 = f QU位置 数值型分组数据的四分位数(计算公式) () (3.10) (3.10) 三、数值型数据集中趋势的测度 (一)算术平均数 算术平均数(Arithmetic mean)也称为均值(Mean),是全部数据算术平均的 结果。算术平均法是计算平均指标最基本、最常用的方法。计算公式为: 总体单位总量 总体标志总量 算术平均数 = 很多社会经济现象,总体标志总量常常是总体单位变量值的算术总和。例如, 4 L L L L L f S Q L i f − = + 4 L L L L L f S Q L i f − 下四分位数: = + 上四分位数 3 4 U U U U U f S Q L i f − = + 3 4 U U U U U f S Q L i f − = +

工人工资总额是总体中每个工人工资的总和,某地区小麦总产量是所有耕地小麦产量的总和。在总体标志总量和总体单位总量的基础上,就可以计算平均指标。算术平均数与强度相对数都是两个总量指标的比值,也都是有名数,都反映了相互联系的两个现象之间的数量对比关系,计算方法也非常相似。但它们却是两个性质不同的统计指标,主要区别有两点:其一,子项指标与母项指标的关系不同。平均数的子项指标与母项指标属于同一个统计总体,是同一统计总体的总体标志总量与总体单位总量的比值,而强度相对数则是来自两个不同总体但有联系的总量指标之比:其二,算术平均数的子项指标(标志总量)随着母项指标(总体单位数)的变动而变动,二者互相适应,而强度相对数的子项指标同母项指标之间不存在这样的关系。算术平均数在统计学中具有重要的地位,是集中趋势的最主要度量值,通常用x(读作x-bar)表示。根据所掌握数据形式的不同,算术平均数有简单算术平均数和加权算术平均数。1.简单算术平均数(Simplearithmeticmean)未经分组整理的原始数据,其算术平均数的计算就是直接将一组数据的各个数值相加除以数值个数。设统计数据为*,2x,则算术平均数的计算公式为:Zx-$+*++x血nn(3.11)【例3.3]某班级40名同学统计学的考试成绩原始资料如表3.1一2所示。表 3. 240名同学统计学原始成绩ABCDEFGHIJ645695981647089798888278896078687979956860378899936758478T647885485797084687589757875该班40名同学统计学的平均成绩为:X= 64+70+.+78+75_330892=77.234040(分)
工人工资总额是总体中每个工人工资的总和,某地区小麦总产量是所有耕地小麦 产量的总和。在总体标志总量和总体单位总量的基础上,就可以计算平均指标。 算术平均数与强度相对数都是两个总量指标的比值,也都是有名数,都反映 了相互联系的两个现象之间的数量对比关系,计算方法也非常相似。但它们却是 两个性质不同的统计指标,主要区别有两点: 其一,子项指标与母项指标的关系不同。平均数的子项指标与母项指标属于 同一个统计总体,是同一统计总体的总体标志总量与总体单位总量的比值,而强 度相对数则是来自两个不同总体但有联系的总量指标之比; 其二,算术平均数的子项指标(标志总量)随着母项指标(总体单位数)的 变动而变动,二者互相适应,而强度相对数的子项指标同母项指标之间不存在这 样的关系。 算术平均数在统计学中具有重要的地位,是集中趋势的最主要度量值,通常 用 x (读作 x bar − )表示。根据所掌握数据形式的不同,算术平均数有简单算术 平均数和加权算术平均数。 1.简单算术平均数(Simple arithmetic mean) 未经分组整理的原始数据,其算术平均数的计算就是直接将一组数据的各个 数值相加除以数值个数。设统计数据为 1 2 x x, , . , n x ,则算术平均数 x 的计算公式 为: 1 2 1 n i n i x x x x x n n + + + = = = (3.11) [例 3.3] 某班级 40 名同学统计学的考试成绩原始资料如表 3.1—2 所示。 表 3.2 40 名同学统计学原始成绩 该班 40 名同学统计学的平均成绩为: 64 70 78 75 3089 77.23 40 40 X + + + + = = = (分)
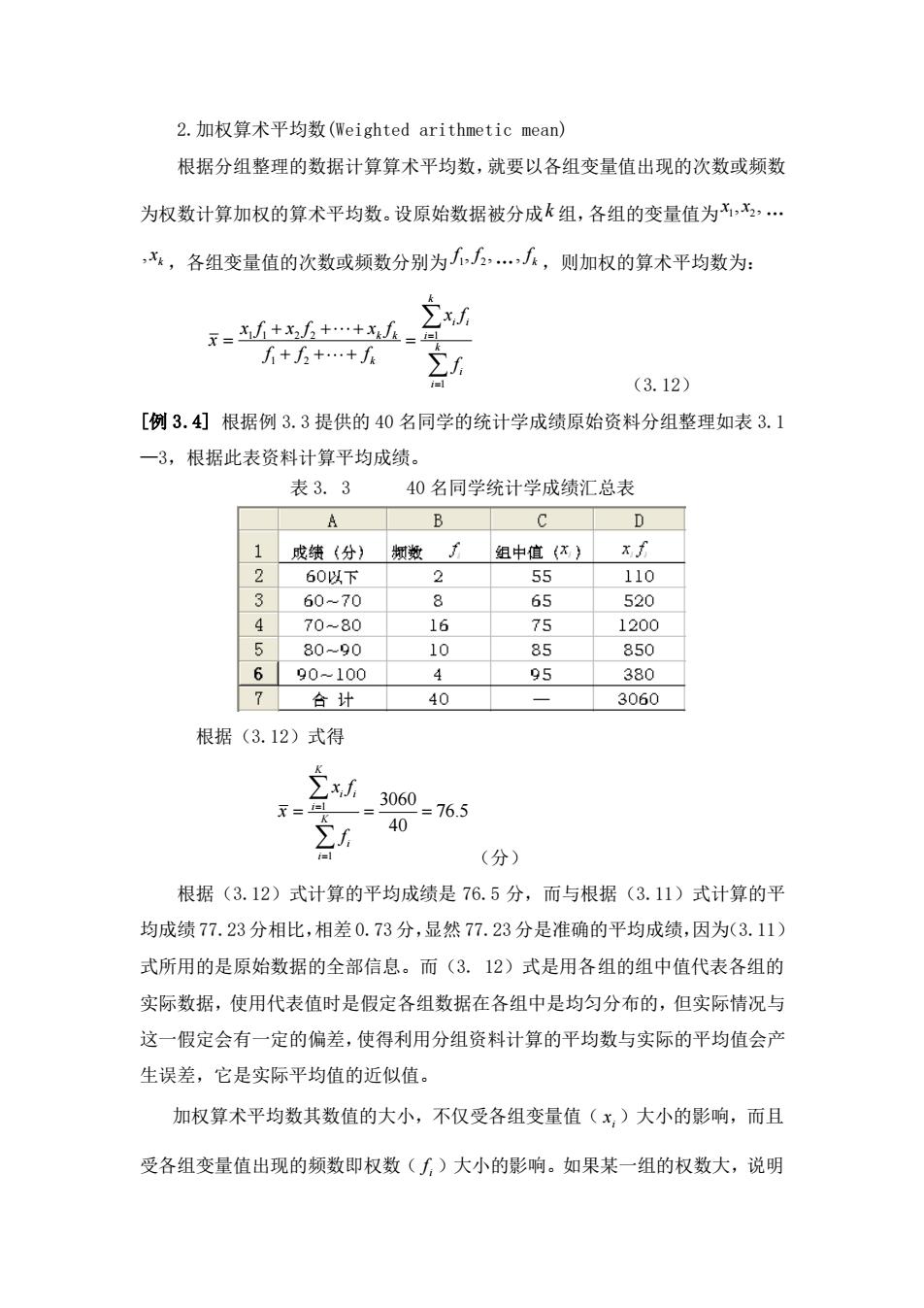
2.加权算术平均数(Weightedarithmeticmean)根据分组整理的数据计算算术平均数,就要以各组变量值出现的次数或频数为权数计算加权的算术平均数。设原始数据被分成k组,各组的变量值为,2x,各组变量值的次数或频数分别为,J2.Je,则加权的算术平均数为:2xJ.+++fi+f++frZ.iel(3.12)[例3.4]根据例3.3提供的40名同学的统计学成绩原始资料分组整理如表3.1一3,根据此表资料计算平均成绩。表3.340名同学统计学成绩汇总表BCDAx手1频数组中值()成绩(分)225511060以下360~70865520470~8016751200580~901085850649590~100380740合计3060根据(3.12)式得Zu3060 =76.5X==l40ZJ.i=l(分)根据(3.12)式计算的平均成绩是76.5分,而与根据(3.11)式计算的平均成绩77.23分相比,相差0.73分,显然77.23分是准确的平均成绩,因为(3.11)式所用的是原始数据的全部信息。而(3.12)式是用各组的组中值代表各组的实际数据,使用代表值时是假定各组数据在各组中是均匀分布的,但实际情况与这一假定会有一定的偏差,使得利用分组资料计算的平均数与实际的平均值会产生误差,它是实际平均值的近似值。加权算术平均数其数值的大小,不仅受各组变量值(x,)大小的影响,而且受各组变量值出现的频数即权数(f)大小的影响。如果某一组的权数大,说明
2.加权算术平均数(Weighted arithmetic mean) 根据分组整理的数据计算算术平均数,就要以各组变量值出现的次数或频数 为权数计算加权的算术平均数。设原始数据被分成 k 组,各组的变量值为 1 2 x x, , . , k x ,各组变量值的次数或频数分别为 1 2 f f , ,., k f ,则加权的算术平均数为: 1 1 2 2 1 1 2 1 k i i k k i k k i i x f x f x f x f x f f f f = = + + + = = + + + (3.12) [例 3.4] 根据例 3.3 提供的 40 名同学的统计学成绩原始资料分组整理如表 3.1 —3,根据此表资料计算平均成绩。 表 3. 3 40 名同学统计学成绩汇总表 根据(3.12)式得 1 1 3060 76.5 40 K i i i K i i x f x f = = = = = (分) 根据(3.12)式计算的平均成绩是 76.5 分,而与根据(3.11)式计算的平 均成绩 77.23 分相比,相差 0.73 分,显然 77.23 分是准确的平均成绩,因为(3.11) 式所用的是原始数据的全部信息。而(3. 12)式是用各组的组中值代表各组的 实际数据,使用代表值时是假定各组数据在各组中是均匀分布的,但实际情况与 这一假定会有一定的偏差,使得利用分组资料计算的平均数与实际的平均值会产 生误差,它是实际平均值的近似值。 加权算术平均数其数值的大小,不仅受各组变量值( i x )大小的影响,而且 受各组变量值出现的频数即权数( i f )大小的影响。如果某一组的权数大,说明

该组的数据较多,那么该组数据的大小对算术平均数的影响就越大,反之,则越小。实际上,我们将(3.12)式变形为下面的形式,就更能清楚地看出这一点。2x.JiX=XZJ.i=lZf.i=li=l(3.13)由(3.13)式可以清楚地看出,加权算术平均数受各组变量值(x)和各组权数即顿率一大小的影响。频率越大,相应的变量值计入平均数的份额也越ZJ.大,对平均数的影响就越大;反之,频率越小,相应的变量值计入平均数的份额也越小,对平均数的影响就越小。这就是权数权衡轻重作用的实质。当我们掌握的权数不是各组变量值出现的频数,而是频率时,可直接根据(4.3.3)式计算算术平均数。如例3.2,根据各组的频数计算的频率分别为:0.05、0.2、0.4、0.25、0.1,各组频率之和为1,则用频率计算的加权算术平均数为:X=i=lEfi=l=55×0.05+65×0.2+75×0.4+85×0.25+95×0.1=76.5(分)从计算结果看,用频率加权计算的结果与用频数加权计算的结果是一致的。需要指出的是,当各组变量值出现的频数(1)或频率一,相等时,权数Zf.的作用就消失了,这就意味着各组变量值对总平均的结果所起的作用是一样的,此时,加权算术平均数就等于简单算术平均数。在实际生活中,我们也会经常遇到由相对数计算平均数的情况。一般地说,求相对数的平均数应采用加权平均的方法,此时,用于加权平均的权数不再是频数或频率,而应根据相对数的含义,选择适当的权数。下面举一个实例说明。[例3.5]某公司所属10个企业资金利润率分组资料如表3.4,要求计算该公司10个企业的平均利润率
该组的数据较多,那么该组数据的大小对算术平均数的影响就越大,反之,则越 小。实际上,我们将(3.12)式变形为下面的形式,就更能清楚地看出这一点。 1 1 1 1 K i i K i i K K i i i i i i x f f x x f f = = = = = = (3.13) 由(3.13)式可以清楚地看出,加权算术平均数受各组变量值( i x )和各组 权数即频率 i i f f 大小的影响。频率越大,相应的变量值计入平均数的份额也越 大,对平均数的影响就越大;反之,频率越小,相应的变量值计入平均数的份额 也越小,对平均数的影响就越小。这就是权数权衡轻重作用的实质。 当我们掌握的权数不是各组变量值出现的频数,而是频率时,可直接根据 (4.3.3)式计算算术平均数。如例 3. 2,根据各组的频数计算的频率分别为: 0.05、0.2、0.4、0.25、0.1,各组频率之和为 1,则用频率计算的加权算术平 均数为: 1 1 55 0.05 65 0.2 75 0.4 85 0.25 95 0.1 K i i K i i i f x x f = = = = + + + + = 76.5 (分) 从计算结果看,用频率加权计算的结果与用频数加权计算的结果是一致的。 需要指出的是,当各组变量值出现的频数( i f )或频率 i i f f 相等时,权数 的作用就消失了,这就意味着各组变量值对总平均的结果所起的作用是一样的, 此时,加权算术平均数就等于简单算术平均数。 在实际生活中,我们也会经常遇到由相对数计算平均数的情况。一般地说, 求相对数的平均数应采用加权平均的方法,此时,用于加权平均的权数不再是频 数或频率,而应根据相对数的含义,选择适当的权数。下面举一个实例说明。 [例 3.5] 某公司所属 10 个企业资金利润率分组资料如表 3.4,要求计算该 公司 10 个企业的平均利润率
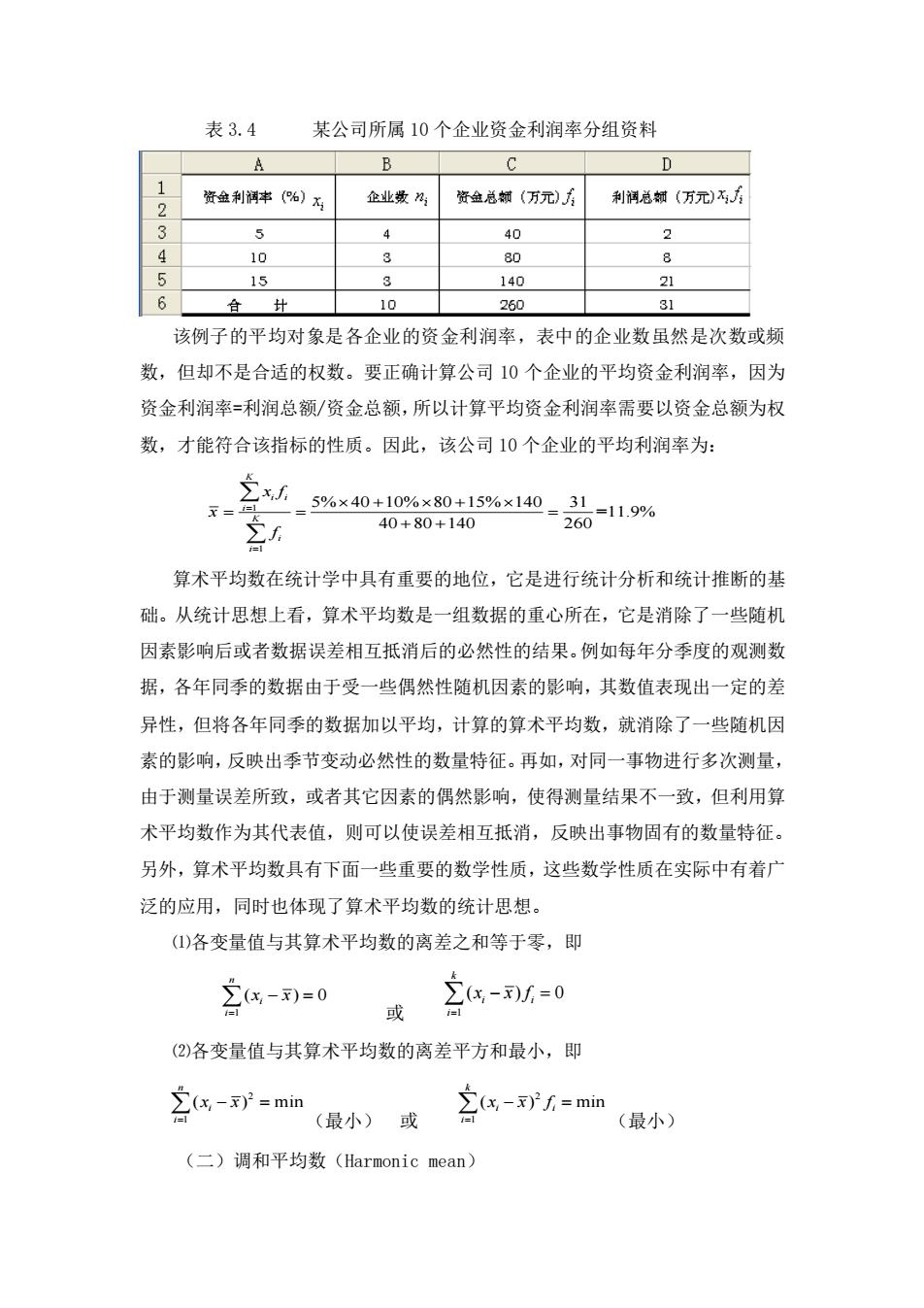
表3.4某公司所属10个企业资金利润率分组资料ABCD1利润总额(万元)企业数n;资金总额(万元)万资金利润率(%)2354402410380853211514061031合计260该例子的平均对象是各企业的资金利润率,表中的企业数虽然是次数或频数,但却不是合适的权数。要正确计算公司10个企业的平均资金利润率,因为资金利润率=利润总额/资金总额,所以计算平均资金利润率需要以资金总额为权数,才能符合该指标的性质。因此,该公司10个企业的平均利润率为:Zx.5%×40 +10%×80+15%×140= 31=11.9%X=El26040+80+1402算术平均数在统计学中具有重要的地位,它是进行统计分析和统计推断的基础。从统计思想上看,算术平均数是一组数据的重心所在,它是消除了一些随机因素影响后或者数据误差相互抵消后的必然性的结果。例如每年分季度的观测数据,各年同季的数据由于受一些偶然性随机因素的影响,其数值表现出一定的差异性,但将各年同季的数据加以平均,计算的算术平均数,就消除了一些随机因素的影响,反映出季节变动必然性的数量特征。再如,对同一事物进行多次测量,由于测量误差所致,或者其它因素的偶然影响,使得测量结果不一致,但利用算术平均数作为其代表值,则可以使误差相互抵消,反映出事物固有的数量特征。另外,算术平均数具有下面一些重要的数学性质,这些数学性质在实际中有着广泛的应用,同时也体现了算术平均数的统计思想。(1)各变量值与其算术平均数的离差之和等于零,即2(g,-),=0Z(x -x)= 0=或(2)各变量值与其算术平均数的离差平方和最小,即Z(x,-x) f =min(x, -x)=min--(最小)或(最小)(二)调和平均数(Harmonicmean)
表 3.4 某公司所属 10 个企业资金利润率分组资料 该例子的平均对象是各企业的资金利润率,表中的企业数虽然是次数或频 数,但却不是合适的权数。要正确计算公司 10 个企业的平均资金利润率,因为 资金利润率=利润总额/资金总额,所以计算平均资金利润率需要以资金总额为权 数,才能符合该指标的性质。因此,该公司 10 个企业的平均利润率为: 1 1 5% 40 10% 80 15% 140 31 =11.9% 40 80 140 260 K i i i K i i x f x f = = + + = = = + + 算术平均数在统计学中具有重要的地位,它是进行统计分析和统计推断的基 础。从统计思想上看,算术平均数是一组数据的重心所在,它是消除了一些随机 因素影响后或者数据误差相互抵消后的必然性的结果。例如每年分季度的观测数 据,各年同季的数据由于受一些偶然性随机因素的影响,其数值表现出一定的差 异性,但将各年同季的数据加以平均,计算的算术平均数,就消除了一些随机因 素的影响,反映出季节变动必然性的数量特征。再如,对同一事物进行多次测量, 由于测量误差所致,或者其它因素的偶然影响,使得测量结果不一致,但利用算 术平均数作为其代表值,则可以使误差相互抵消,反映出事物固有的数量特征。 另外,算术平均数具有下面一些重要的数学性质,这些数学性质在实际中有着广 泛的应用,同时也体现了算术平均数的统计思想。 ⑴各变量值与其算术平均数的离差之和等于零,即 1 ( ) 0 n i i x x = − = 或 1 ( ) 0 k i i i x x f = − = ⑵各变量值与其算术平均数的离差平方和最小,即 2 1 ( ) min n i i x x = − = (最小) 或 2 1 ( ) min k i i i x x f = − = (最小) (二)调和平均数(Harmonic mean)