
第五章统计指数(一)教学目的通过本章的学习,使学生正确理解指数的概念和作用,从而掌握各种指数的编制原理和计算方法。(二)基本要求要求掌握指数的概念、性质、种类和作用,学会编制综合指数、平均数指数及平均指标指数,并能将不同的指数区分开来,进一步学会利用指数体系进行因素分析。(三)教学要点1、指数的概念与种类;2、总指数的编制方法:3、平均指标指数的编制方法;4、指数体现与因素分析:5、指数数列的编制及类型。(四)本章难点1、广义指数与狭义指数的区分;2、数量指数与质量指数的区分;3、指数化因素与同度量因素的区分;4、综合指数与平均数指数的联系:5、平均数指与平均指标指数的区分。(五)教学时数6—8课时(六)教学内容本章共分四节:第一节统计指数概述一、统计指数的概念广义上说,指数是指用来反映研究所研究社会经济现象总体数量变动状况的相对
第五章 统计指数 (一)教学目的 通过本章的学习,使学生正确理解指数的概念和作用,从而掌握各种指数的编制原 理和计算方法。 (二)基本要求 要求掌握指数的概念、性质、种类和作用,学会编制综合指数、平均数指数及平均 指标指数,并能将不同的指数区分开来,进一步学会利用指数体系进行因素分析。 (三)教学要点 1、指数的概念与种类; 2、总指数的编制方法; 3、平均指标指数的编制方法; 4、指数体现与因素分析; 5、指数数列的编制及类型。 (四)本章难点 1、广义指数与狭义指数的区分; 2、数量指数与质量指数的区分; 3、指数化因素与同度量因素的区分; 4、综合指数与平均数指数的联系; 5、平均数指与平均指标指数的区分。 (五)教学时数 6—8 课时 (六)教学内容 本章共分四节: 第一节 统计指数概述 一、统计指数的概念 广义上说,指数是指用来反映研究所研究社会经济现象总体数量变动状况的相对

数。狭义上说,指数是指用来综合反映所研究社会经济现象复杂总体数量变动状况的相对数。二、 统计指数的分类按所反映的对象范围不同,统计指数分为个体指数和总指数。按所表明现象的数量特征不同,统计指数分为数量指标指数和质量指标指数。总指数按其所采用的指标形式不同,可以分为综合指数与平均指数。按比较对象不同,统计指数可分时间性指数、地区性指数和计划完成指数。在指数数列中按所采用的基期不同,统计指数可分为定基指数和环比指数三、统计指数的性质1.综合性。2.代表性。3.相对性。4.平均性。四、指数在经济分析中的作用1.综合地反映复杂经济现象总体的变动方向和程度。2.分析在现象总体的变动中,各构成因素影响的大小。第二节乡综合指数一、综合指数的概念及计算的一般原理指数方法论主要是研究总指数的计算问题,总指数的编制方法,其基本形式有两种:一是综合指数,二是平均指数。两种方法有一定的联系,但各有其特点。综合指数是对两个时期范围相同的复杂现象总体总量指标对比形成的指数,在总量指标中包含两个或两个以上的因素,将其中被研究因素以外的一个或一个以上的因素适定下来,仅观察被研究因素的变动,这样编制的指数,称为综合指数。综合指数的重要意义,是它能够比较全面、准确地反映所研究的现象总体总的变动程度和随之产生的绝对数效果。它的特点是先综合后对比。其编制方法是:首先引入同度量因素,解决复杂总体在研究指标上不能直接综合的困难,使其可以计算出总体的综合总量;其次,将同度量因素固定,以消除同度量因素变动的影响;最后将两个时期的总量对比,其结果即为综合1
1 数。 狭义上说,指数是指用来综合反映所研究社会经济现象复杂总体数量变动状况的相 对数。 二、统计指数的分类 按所反映的对象范围不同,统计指数分为个体指数和总指数。 按所表明现象的数量特征不同,统计指数分为数量指标指数和质量指标指数。 总指数按其所采用的指标形式不同,可以分为综合指数与平均指数。 按比较对象不同,统计指数可分时间性指数、地区性指数和计划完成指数。 在指数数列中按所采用的基期不同,统计指数可分为定基指数和环比指数。 三、统计指数的性质 1.综合性。 2.代表性。 3.相对性。 4.平均性。 四、指数在经济分析中的作用 1.综合地反映复杂经济现象总体的变动方向和程度。 2.分析在现象总体的变动中,各构成因素影响的大小。 第二节 综合指数 一、综合指数的概念及计算的一般原理 指数方法论主要是研究总指数的计算问题,总指数的编制方法,其基本形式有两种: 一是综合指数,二是平均指数。两种方法有一定的联系,但各有其特点。 综合指数是对两个时期范围相同的复杂现象总体总量指标对比形成的指数,在总量 指标中包含两个或两个以上的因素,将其中被研究因素以外的一个或一个以上的因素固 定下来,仅观察被研究因素的变动,这样编制的指数,称为综合指数。 综合指数的重要意义,是它能够比较全面、准确地反映所研究的现象总体总的变动 程度和随之产生的绝对数效果。 它的特点是先综合后对比。其编制方法是:首先引入同度量因素,解决复杂总体在 研究指标上不能直接综合的困难,使其可以计算出总体的综合总量;其次,将同度量因 素固定,以消除同度量因素变动的影响;最后将两个时期的总量对比,其结果即为综合

指数,也就综合地反映了复杂总体研究指标的变动。例如甲乙两种产品,由于使用价值不同,计量单位不同,其产量是不能直接相加的,但不同产品的价值量可以相加。因此,我们可以利用产值与产量和价格之间的联系,将产量乘以各自的价格,得到产值,则两种产品便可以加总了。这里,价格起到将不同产品同度量的作用,被称为同度量因素。我们所要研究的指标一一产量,被称为指数化指标。如果我们的任务是研究甲乙两种产品的价格变动情况,同样的道理,则可把价格作为指数化指标,仍然依据产值、价格与产量间的经济联系,把产量作为同度量因素,从而将两种产品综合起来。同时还要将同度量因素固定,消除同度量因素变动的影响。在本例中,作为同度量因素的价格,报告期对基期也可能发生变动,这样,将两个时期的产值对比,就不仅受到产品产量变动的影响,同时也受到两个时期价格变动的影响。因此,需要将价格固定,即两个时期的产值,均采用同一时期的价格计算,借以消除价格变动的影响。将采用同一时期价格计算的两个产值对比,其结果仅受到两种产品不同时期产量变动的影响,从而达到综合反映两种产品产量变动的目的。实际应用中,还有一个重要的问题需要解决,即固定的同度量因素所属时期的选择问题。究竞固定在报告期还是固定在基期,十分重要,因为同度量因素不仅起同度量的作用,而且具有加权的作用,用不同时期的同度量因素计算,会得到不同的综合指数结果。二、数量指标综合指数的编制现以商品销售量综合指数的编制为例来说明数量指标综合指数编制的一般原则和方法。现以I代表销售量总指数,于是有:(1)用基期价格为同度量因素(加权),公式为:ZqiPoIg=ZqoPo上述公式又称拉氏数量指数公式,它是1864年由德国学者拉斯贝尔提出的。(2)用报告期价格为同度量因素(加权),公式为:ZqpiI.=Zqop这个公式又称派氏数量指数公式,它是1874年德国学者派许提出的。从理论上讲上述两个公式均可成立,但在实际工作中,编制销售量综合指数时,一般均采用基期价格作为同度量因素。这是因为编制销售量综合指数的目的,是在于要排2
2 指数,也就综合地反映了复杂总体研究指标的变动。 例如甲乙两种产品,由于使用价值不同,计量单位不同,其产量是不能直接相加的, 但不同产品的价值量可以相加。因此,我们可以利用产值与产量和价格之间的联系,将 产量乘以各自的价格,得到产值,则两种产品便可以加总了。这里,价格起到将不同产 品同度量的作用,被称为同度量因素。我们所要研究的指标——产量,被称为指数化指 标。如果我们的任务是研究甲乙两种产品的价格变动情况,同样的道理,则可把价格作 为指数化指标,仍然依据产值、价格与产量间的经济联系,把产量作为同度量因素,从 而将两种产品综合起来。同时还要将同度量因素固定,消除同度量因素变动的影响。在 本例中,作为同度量因素的价格,报告期对基期也可能发生变动,这样,将两个时期的 产值对比,就不仅受到产品产量变动的影响,同时也受到两个时期价格变动的影响。因 此,需要将价格固定,即两个时期的产值,均采用同一时期的价格计算,借以消除价格 变动的影响。将采用同一时期价格计算的两个产值对比,其结果仅受到两种产品不同时 期产量变动的影响,从而达到综合反映两种产品产量变动的目的。实际应用中,还有一 个重要的问题需要解决,即固定的同度量因素所属时期的选择问题。究竟固定在报告期 还是固定在基期,十分重要,因为同度量因素不仅起同度量的作用,而且具有加权的作 用,用不同时期的同度量因素计算,会得到不同的综合指数结果。 二、数量指标综合指数的编制 现以商品销售量综合指数的编制为例来说明数量指标综合指数编制的一般原则和 方法。 现以Iq代表销售量总指数,于是有: (1)用基期价格为同度量因素(加权),公式为: = 0 0 1 0 q p q p I q 上述公式又称拉氏数量指数公式,它是1864年由德国学者拉斯贝尔提出的。 (2)用报告期价格为同度量因素(加权),公式为: = 0 1 1 1 q p q p I q 这个公式又称派氏数量指数公式,它是1874年德国学者派许提出的。 从理论上讲上述两个公式均可成立,但在实际工作中,编制销售量综合指数时,一 般均采用基期价格作为同度量因素。这是因为编制销售量综合指数的目的,是在于要排
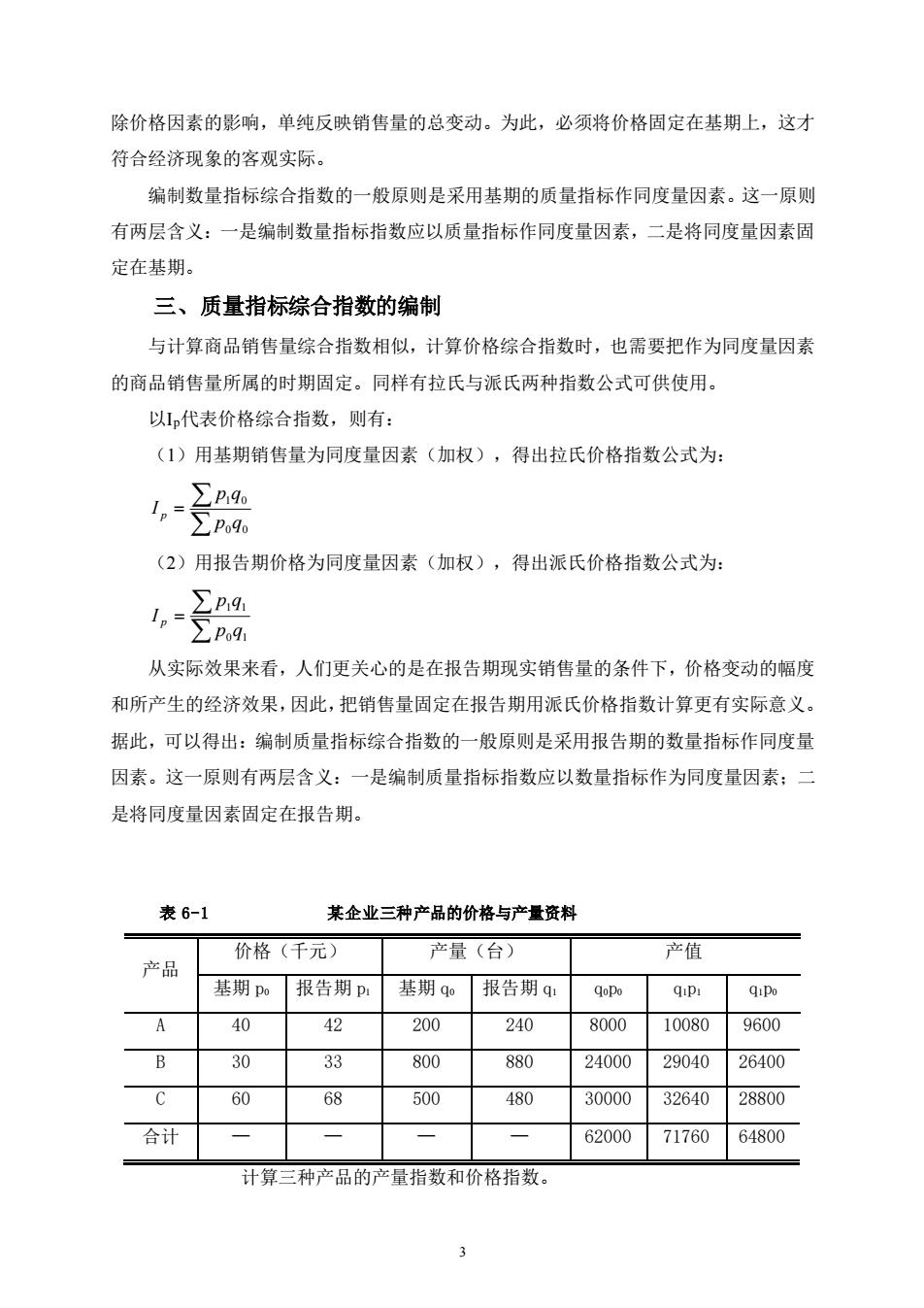
除价格因素的影响,单纯反映销售量的总变动。为此,必须将价格固定在基期上,这才符合经济现象的客观实际。编制数量指标综合指数的一般原则是采用基期的质量指标作同度量因素。这一原则有两层含义:一是编制数量指标指数应以质量指标作同度量因素,二是将同度量因素固定在基期。三、质量指标综合指数的编制与计算商品销售量综合指数相似,计算价格综合指数时,也需要把作为同度量因素的商品销售量所属的时期固定。同样有拉氏与派氏两种指数公式可供使用。以Ip代表价格综合指数,则有:(1)用基期销售量为同度量因素(加权),得出拉氏价格指数公式为:ZpidoI,=Zpoqo(2)用报告期价格为同度量因素(加权),得出派氏价格指数公式为:EpigIp=Epogi从实际效果来看,人们更关心的是在报告期现实销售量的条件下,价格变动的幅度和所产生的经济效果,因此,把销售量固定在报告期用派氏价格指数计算更有实际意义。据此,可以得出:编制质量指标综合指数的一般原则是采用报告期的数量指标作同度量因素。这一原则有两层含义:一是编制质量指标指数应以数量指标作为同度量因素;二是将同度量因素固定在报告期。表 6-1某企业三种产品的价格与产量资料产量(台)产值价格(千元)产品基期po报告期p基期qo报告期q1qopoqipiqipoA40422002409600800010080B3033264008008802400029040c6068500480300003264028800合计648006200071760-计算三种产品的产量指数和价格指数。3
3 除价格因素的影响,单纯反映销售量的总变动。为此,必须将价格固定在基期上,这才 符合经济现象的客观实际。 编制数量指标综合指数的一般原则是采用基期的质量指标作同度量因素。这一原则 有两层含义:一是编制数量指标指数应以质量指标作同度量因素,二是将同度量因素固 定在基期。 三、质量指标综合指数的编制 与计算商品销售量综合指数相似,计算价格综合指数时,也需要把作为同度量因素 的商品销售量所属的时期固定。同样有拉氏与派氏两种指数公式可供使用。 以Ip代表价格综合指数,则有: (1)用基期销售量为同度量因素(加权),得出拉氏价格指数公式为: = 0 0 1 0 p q p q I p (2)用报告期价格为同度量因素(加权),得出派氏价格指数公式为: = 0 1 1 1 p q p q I p 从实际效果来看,人们更关心的是在报告期现实销售量的条件下,价格变动的幅度 和所产生的经济效果,因此,把销售量固定在报告期用派氏价格指数计算更有实际意义。 据此,可以得出:编制质量指标综合指数的一般原则是采用报告期的数量指标作同度量 因素。这一原则有两层含义:一是编制质量指标指数应以数量指标作为同度量因素;二 是将同度量因素固定在报告期。 表 6-1 某企业三种产品的价格与产量资料 产品 价格(千元) 产量(台) 产值 基期 p0 报告期 p1 基期 q0 报告期 q1 q0p0 q1p1 q1p0 A 40 42 200 240 8000 10080 9600 B 30 33 800 880 24000 29040 26400 C 60 68 500 480 30000 32640 28800 合计 — — — — 62000 71760 64800 计算三种产品的产量指数和价格指数

产量指数:EqPo-648002=104.52%I.:62000ZqoPo说明报告期与基期相比,三种产品的产量增加了4.52%。ZqiPo-qoP。=64800-62000=2800(千元)说明报告期与基期相比,三种产品的产量增加了4.52%,而使得产值增加了2800000元。价格指数:ZqiPl_ 71760 =110.74%I,一Zqipo64800说明报告期与基期相比,三种产品的价格上涨了10.74%。ZqiP,-ZqiP。=71760-64800=6960(千元)说明报告期与基期相比,三种产品的价格上涨了10.7%,而使得产值增加了6960000元。四、综合指数的应用综合指数的应用很广,在我国和其他各国,都有很多指数采用这种方法计算。下面来考察常用的几个方面。(一)工业产量(产值)指数我国现行统计制度规定,工业总产值按统一规定的不变价格计算。于是,把不同年份的工业总产值对比所确定的动态指标,就是工业产量指数。它是以不变价格为权数(同度量因素)的固定加权综合的指数,用公式表示如下:ZqP,IgZqoP.Pn表示不变价格;qPn表示按不变价格计算的工业总产值。用按不变价格计算的工业总产值来编制工业产量指数,具有如下优点:(1)便于长时期工业产量动态分析,观察工业产值增长变化趋势及其规律性。(2)环比指数数列的连乘积等于定基指数,因而便于定基指数和环比指数之间的相互换算。4
4 产量指数: 104.52% 62000 64800 0 0 1 0 = = = q p q p I q 说明报告期与基期相比,三种产品的产量增加了4.52%。 q1 p0 −q0 p 0 = 64800 − 62000 = 2800(千元) 说明报告期与基期相比,三种产品的产量增加了4.52%,而使得产值增加了 2800000元。 价格指数: 110.74% 64800 71760 1 0 1 1 = = = q p q p I p 说明报告期与基期相比,三种产品的价格上涨了10.74%。 q1 p1 −q1 p 0 = 71760 − 64800 = 6960(千元) 说明报告期与基期相比,三种产品的价格上涨了10.7%,而使得产值增加了 6960000元。 四、综合指数的应用 综合指数的应用很广,在我国和其他各国,都有很多指数采用这种方法计算。下面 来考察常用的几个方面。 (一)工业产量(产值)指数 我国现行统计制度规定,工业总产值按统一规定的不变价格计算。于是,把不同年 份的工业总产值对比所确定的动态指标,就是工业产量指数。它是以不变价格为权数(同 度量因素)的固定加权综合的指数,用公式表示如下: = n n q q p q p I 0 1 pn表示不变价格; qpn表示按不变价格计算的工业总产值。 用按不变价格计算的工业总产值来编制工业产量指数,具有如下优点: (1) 便于长时期工业产量动态分析,观察工业产值增长变化趋势及其规律性。 (2) 环比指数数列的连乘积等于定基指数,因而便于定基指数和环比指数之间的相 互换算