
第三章统计描述(一)教学目的通过本章的学习,使同学们正确理解各种指标的概念及计算方法,学会运用相应的统计指标对数据的分布特征进行分析说明。(二)基本要求使学生熟练掌握数据分布特征的描述方法。(三)教学要点1、集中趋势的测度指标及其计算方法:2、离散趋势的测度指标及其计算方法:3、总体分布的偏度与峰度的测度。(四)本章难点1、集中趋势指标的计算方法与应用场合;2、离散趋势指标的计算方法与应用场合;3、如何正确运用离散趋势指标评价总体平均水平的代表性;4、对标准差、方差等指标含义的准确理解。5、偏度与峰度指标的计算方法与应用场合。(五)教学时数9——10课时(六)学习内容本章共分三节:第一节分布的集中趋势一、定类数据集中趋势的测度一一众数(Mode)(一)概念要点众数是指一组数据中出现次数最多的变量值,用M。表示。从变量分布的角度看,众数是具有明显集中趋势点的数值,一组数据分布的最高峰点所对应的数值即为众数。当然,如果数据的分布没有明显的集中趋势或最高峰点,众数也可以不存在;如果有多个高峰点,也就有多个众数。1.集中趋势的测度值之一
第三章 统计描述 (一)教学目的 通过本章的学习,使同学们正确理解各种指标的概念及计算方法,学会运用 相应的统计指标对数据的分布特征进行分析说明。 (二)基本要求 使学生熟练掌握数据分布特征的描述方法。 (三)教学要点 1、集中趋势的测度指标及其计算方法; 2、离散趋势的测度指标及其计算方法; 3、总体分布的偏度与峰度的测度。 (四)本章难点 1、集中趋势指标的计算方法与应用场合; 2、离散趋势指标的计算方法与应用场合; 3、如何正确运用离散趋势指标评价总体平均水平的代表性; 4、对标准差、方差等指标含义的准确理解。 5、偏度与峰度指标的计算方法与应用场合。 (五)教学时数 9——10 课时 (六)学习内容 本章共分三节: 第一节 分布的集中趋势 一、定类数据集中趋势的测度——众数(Mode) (一) 概念要点 众数是指一组数据中出现次数最多的变量值,用 M o 表示。从变量分布的角 度看,众数是具有明显集中趋势点的数值,一组数据分布的最高峰点所对应的数 值即为众数。当然,如果数据的分布没有明显的集中趋势或最高峰点,众数也可 以不存在;如果有多个高峰点,也就有多个众数。 1.集中趋势的测度值之一

2.出现次数最多的变量值3.不受极端值的影响4.可能没有众数或有几个众数5.主要用于定类数据,也可用于定序数据和数值型数据众数的不唯一性:10591268无众数原始数据:6 59855一个众数原始数据:252828364242多于一个众数原始数据:(二)众数的计算根据未分组数据或单变量值分组数据计算众数时,我们只需找出出现次数最多的变量值即为众数。对于组距分组数据,众数的数值与其相邻两组的频数分布有一定的关系,这种关系可作如下的理解:设众数组的频数为fm,众数前一组的频数为f-,众数后一组的频数为f。当众数相邻两组的频数相等时,即f-=,众数组的组中值即为众数;当众数组的前一组的频数多于众数组后一组的频数时,即f.,>f.,则众数会向其前一组靠,众数小于其组中值;当众数组后一组的频数多于众数组前一组的频数时,即f-<于,则众数会向其后一组靠,众数大于其组中值。基于这种思路,借助于几何图形而导出的分组数据众数的计算公式如下:下限公式:Jm-fxd=L+_AxdM。= L+(fm-f.)+(fm - J.)4; +42(3. 1)上限公式:Jm- f.i-×d=U--xdM。=U-(fm - f-)+(fm - ff)4; +42(3. 2)式中:L表示众数所在组的下限;U表示众数所在组的上限;d表示众数所在组的组距。【例3.1]现利用表3.1一1资料计算3000户农民家庭年人均收入的众数
2.出现次数最多的变量值 3.不受极端值的影响 4.可能没有众数或有几个众数 5.主要用于定类数据,也可用于定序数据和数值型数据 众数的不唯一性: 无众数原始数据: 10 5 9 12 6 8 一个众数原始数据: 6 5 9 8 5 5 多于一个众数原始数据: 25 28 28 36 42 42 (二)众数的计算 根据未分组数据或单变量值分组数据计算众数时,我们只需找出出现次数最 多的变量值即为众数。对于组距分组数据,众数的数值与其相邻两组的频数分布 有一定的关系,这种关系可作如下的理解: 设众数组的频数为 m f ,众数前一组的频数为 −1 f ,众数后一组的频数为 +1 f 。 当众数相邻两组的频数相等时,即 −1 f = +1 f ,众数组的组中值即为众数;当众数 组的前一组的频数多于众数组后一组的频数时,即 −1 f > +1 f ,则众数会向其前一 组靠,众数小于其组中值;当众数组后一组的频数多于众数组前一组的频数时, 即 −1 f < +1 f ,则众数会向其后一组靠,众数大于其组中值。基于这种思路,借助 于几何图形而导出的分组数据众数的计算公式如下: 下限公式: 1 1 1 1 1 2 ( ) ( ) m o m m f f M L d L d f f f f − − + − = + = + − + − + (3.1) 上限公式: 1 2 1 1 1 2 ( ) ( ) m o m m f f M U d U d f f f f + − + − = − = − − + − + (3.2) 式中: L 表示众数所在组的下限; U 表示众数所在组的上限; d 表示众数所在组的组距。 [例 3.1] 现利用表 3.1—1 资料计算 3000 户农民家庭年人均收入的众数
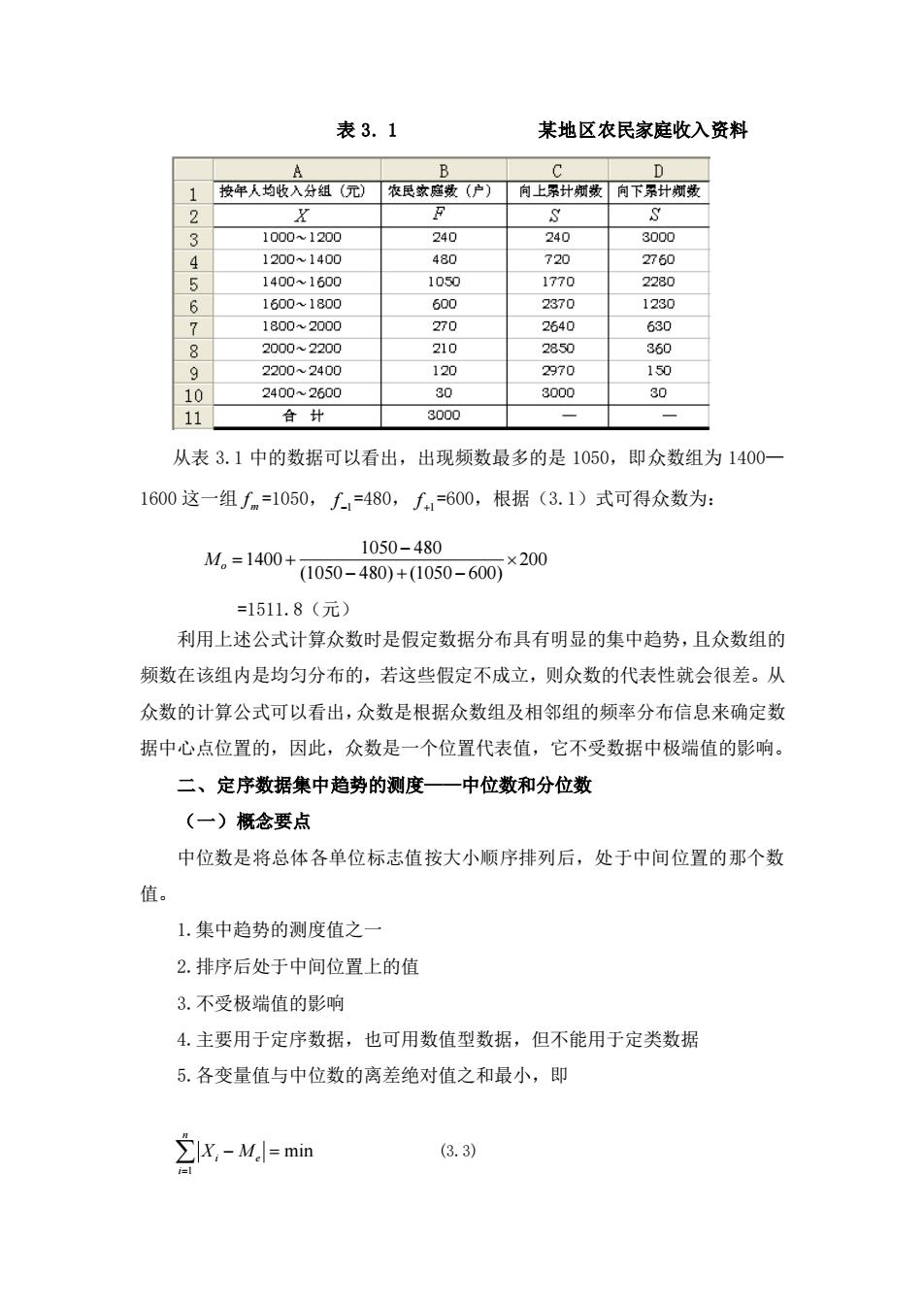
表3.1某地区农民家庭收入资料BDCA按人均收入分组(元)农民家庭数(户)向上累计频数向下累计频数!1FSs2X24024031000~120030001200~1400480720276041050177022801400~1600560023701600~180012306270264063071800~200021028.5036082000~220012015092200~240029702400~2600303000301011合计3000从表3.1中的数据可以看出,出现频数最多的是1050,即众数组为1400-1600这一组fm=1050,f-,=480,f.=600,根据(3.1)式可得众数为:1050-480×200M。=1400+(1050-480)+(1050-600)=1511.8(元)利用上述公式计算众数时是假定数据分布具有明显的集中趋势,且众数组的频数在该组内是均匀分布的,若这些假定不成立,则众数的代表性就会很差。从众数的计算公式可以看出,众数是根据众数组及相邻组的频率分布信息来确定数据中心点位置的,因此,众数是一个位置代表值,它不受数据中极端值的影响。二、定序数据集中趋势的测度一一中位数和分位数(一)概念要点中位数是将总体各单位标志值按大小顺序排列后,处于中间位置的那个数值。1.集中趋势的测度值之一2.排序后处于中间位置上的值3.不受极端值的影响4.主要用于定序数据,也可用数值型数据,但不能用于定类数据5.各变量值与中位数的离差绝对值之和最小,即Z|X,- M]= min(3. 3)=l
表 3. 1 某地区农民家庭收入资料 从表 3.1 中的数据可以看出,出现频数最多的是 1050,即众数组为 1400— 1600 这一组 m f =1050, −1 f =480, +1 f =600,根据(3.1)式可得众数为: 1050 480 1400 200 (1050 480) (1050 600) M o − = + − + − =1511.8(元) 利用上述公式计算众数时是假定数据分布具有明显的集中趋势,且众数组的 频数在该组内是均匀分布的,若这些假定不成立,则众数的代表性就会很差。从 众数的计算公式可以看出,众数是根据众数组及相邻组的频率分布信息来确定数 据中心点位置的,因此,众数是一个位置代表值,它不受数据中极端值的影响。 二、定序数据集中趋势的测度——中位数和分位数 (一)概念要点 中位数是将总体各单位标志值按大小顺序排列后,处于中间位置的那个数 值。 1.集中趋势的测度值之一 2.排序后处于中间位置上的值 3.不受极端值的影响 4.主要用于定序数据,也可用数值型数据,但不能用于定类数据 5.各变量值与中位数的离差绝对值之和最小,即 1 min n i e i X M = − = (3.3)

(二)中位数的计算根据未分组资料和分组资料都可确定中位数。有三种情况:1.对于未分组的原始资料,首先必须将标志值按大小排序。设排序的结果为:X≤x≤X≤.≤则中位数就可以按下面的方式确定:(3. 4)Me=Xa,当n为奇数2x.+x.+2当n为偶数(3. 5)Me=22.对于单项式变量数列资料,由于变量值以及序列化,故中位数可以直接按下面的方式确定:XEl,当Zf为奇数(3. 6)2Me=X+XE当Zf为偶数(3.7)23.对于组距式变量数列,确定中位数也需要分两步进行:(1)从变量数列的累计频数栏中找出第Zf个单位所在的组,即“中位数2组”,该组的上、下限就规定了中位数的可能取值范围:(2)假定在中位数组内的各单位是均匀分布的,就可利用下面的公式计算中位数的近似值:ZfSMe-12Me = L.dMeX(3. 8)fMe
(二)中位数的计算 根据未分组资料和分组资料都可确定中位数。有三种情况: 1.对于未分组的原始资料,首先必须将标志值按大小排序。设排序的结果为: 1 2 3 n x x x x 则 中位数就可以按下面的方式确定: Me= 1 2 x n+ ,当 n 为奇数 (3.4) Me= 1 2 2 2 x x n n + + ,当 n 为偶数 (3.5) 2.对于单项式变量数列资料,由于变量值以及序列化,故中位数可以直接按 下面的方式确定: 1 2 x f + ,当 f 为奇数 (3.6) Me= 1 2 2 2 x x f f + + ,当 f 为偶数 (3.7) 3.对于组距式变量数列,确定中位数也需要分两步进行: (1)从变量数列的累计频数栏中找出第 2 f 个单位所在的组,即“中位数 组”,该组的上、下限就规定了中位数的可能取值范围; (2)假定在中位数组内的各单位是均匀分布的,就可利用下面的公式计算 中位数的近似值: 1 2 Me Me Me Me f s Me L d f − − = + (3.8)

Zf.S Me+12=U.dMe(3. 9)Mf Me上面两式分别称作中位数的“下限公式”。式中,SMe-}是到中位数组前面一组为止的向上累计频数,SMe+1则是到中位数组后面一组为止的向下累计频数;dMe=UMe-LMe为中位数组的组距。(三)分位数中位数是从中间点将全部数据等分为两部分。与中位数类似的还有四分位数(quartile)、十分位数(decile)和百分位数(percentile)等。它们分别是用3个点、9个点和99个点将数据四等分、10等分和100等分后各分位点上的值。这里只介绍四分位数的计算,其他分位数与之类似。一组数据排序后处于25%和75%位置上的值,称为四分位数,也称四分位点。四分位数是通过三个点将全部数据等分为四部分,其中每部分包含25%的数据。很显然,中间的四分位数就是中位数,因此通常所说的四分位数是指处在25%位置上的数值(下四分位数)和处在75%位置上的数值(上四分位数)。与中位数的计算方法类似,根据未分组数据计算四分位数时,首先对数据进行排序,然后确定四分位数所在的位置。1.四分位数位置的确定设下四分位数为QL,上四分位数为QU,对于未分组的原始数据,各四分位数的位置分别为:(1)未分组数据:Q,位置=3(n+I)Q,位置=n+1X4当四分位数的位置不在某一个位置上时,可根据四分位数的位置,按比例分摊四分位数两侧的差值。[例3.2]在某城市中随机抽取9个家庭,调查得到每个家庭的人均月收入数
1 2 Me Me Me Me f s U d f + − = − (3.9) 上面两式分别称作中位数的“下限公式”。式中, Me 1 s − 是到中位数组前 面一组为止的向上累计频数, Me 1 s + 则是到中位数组后面一组为止的向下累计频 数; Me d =UMe − LMe 为中位数组的组距。 (三)分位数 中位数是从中间点将全部数据等分为两部分。与中位数类似的还有四分位数 (quartile)、十分位数(decile)和百分位数(percentile)等。它们分别是 用 3 个点、9 个点和 99 个点将数据四等分、10 等分和 100 等分后各分位点上的 值。这里只介绍四分位数的计算,其他分位数与之类似。 一组数据排序后处于 25%和 75%位置上的值,称为四分位数,也称四分位 点。 四分位数是通过三个点将全部数据等分为四部分,其中每部分包含 25%的 数据。很显然,中间的四分位数就是中位数,因此通常所说的四分位数是指处在 25%位置上的数值(下四分位数)和处在 75%位置上的数值(上四分位数)。与 中位数的计算方法类似,根据未分组数据计算四分位数时,首先对数据进行排序, 然后确定四分位数所在的位置。 1.四分位数位置的确定 设下四分位数为 QL ,上四分位数为QU,对于未分组的原始数据,各四分 位数的位置分别为: (1)未分组数据: u n+1 3(n+1) Q 4 4 QL位置 位置= = 当四分位数的位置不在某一个位置上时,可根据四分位数的位置,按比例分摊四 分位数两侧的差值。 [例 3.2]在某城市中随机抽取 9 个家庭,调查得到每个家庭的人均月收入数