
二、双组分理想物系的气液平衡 ·液相为理想液体,服从拉乌尔定律 ■气相为理想气体,服从理想气体定律
二、双组分理想物系的气液平衡 液相为理想液体,服从拉乌尔定律 气相为理想气体,服从理想气体定律

1.拉乌尔定律 对于理想溶液,在一定温度下: PA=PxA P8 paxB=pB(1-xA) PA,PB-溶液上方组分A及B的平衡分压 p,p8-纯组分A,B的饱和蒸气压 x4,x溶液中组分A,B的摩尔分数 纯组分的饱和蒸气压是温度的函数,通常用阿托因方 程表示:A了丹C
1. 拉乌尔定律 A B x ,x A,B -溶液中组分 的摩尔分数 对于理想溶液,在一定温度下: 0 A A A p p x 0 0 (1 ) p p x p x B B B B A , p p A B A B 溶液上方组分 及 的平衡分压 0 0 , p p A,B A B 纯组分 的饱和蒸气压 0 lg B p A T C 纯组分的饱和蒸气压是温度的函数,通常用阿托因方 程表示:

2.泡点方程 当溶液沸腾时,各组分蒸气压之和等于系统压力 P=Pa+PB Paxa+PexB Pxa+pe(1-xA) 用x表示其中的易挥发组分,并略去下标: P-P8 p-pR(T) X三 p2-pe p(T)-PR(T) 上式是理想物系的液相组成与温度(泡点)关系
2. 泡点方程 0 0 0 0 0 0 ( ) ( ) ( ) B B A B A B p p p p T x p p p T p T 当溶液沸腾时,各组分蒸气压之和等于系统压力 0 0 0 0 (1 ) p p p p x p x p x p x A B A A B B A A B A 用 x 表示其中的易挥发组分,并略去下标: 上式是理想物系的液相组成与温度(泡点)关系

3.露点方程 根据道尔顿分压定律,组分A在蒸气相中的分率 p p 由泡点方程得:x=PP-p-p(I) p%-p8p(T)-p(T) y=23 p- p2=p9(T)p-p(T) P P-P PP(T)-pR(T) 上式是理想物系的气相组成与温度(露点)关系
3. 露点方程 0 0 0 0 0 0 0 0 ( ) ( ) ( ) ( ) A A A A A B A B p p p p T p p T y p p p p p T p T 根据道尔顿分压定律,组分 A 在蒸气相中的分率 0 A A A A p p x y p p 0 0 0 0 0 0 ( ) ( ) ( ) B B A B A B p p p p T x p p p T p T 由泡点方程得: 上式是理想物系的气相组成与温度(露点)关系
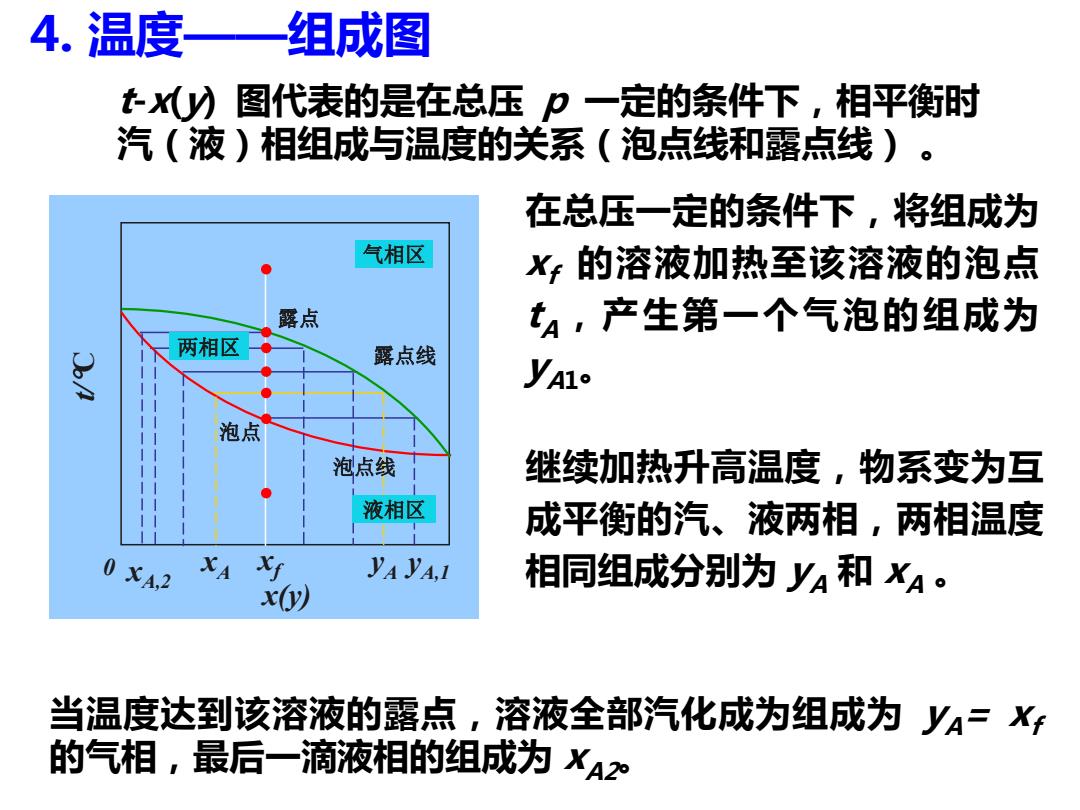
4.温度——组成图 七)图代表的是在总压p一定的条件下,相平衡时 汽(液)相组成与温度的关系(泡点线和露点线)。 在总压一定的条件下,将组成为 气相区 X的溶液加热至该溶液的泡点 露点 t4,产生第一个气泡的组成为 两相区 露点线 VA1e 泡点 泡点线 继续加热升高温度,物系变为互 液相区 成平衡的汽、液两相,两相温度 0XA,2 XA yAYA,I 相同组成分别为y4和X4。 x(y) 当温度达到该溶液的露点,溶液全部汽化成为组成为y4=X+ 的气相,最后一滴液相的组成为X42
t/ C x(y) 0 露点线 泡点线 露点 泡点 xA yA xf 气相区 液相区 两相区 t-x(y) 图代表的是在总压 p 一定的条件下,相平衡时 汽(液)相组成与温度的关系(泡点线和露点线) 。 在总压一定的条件下,将组成为 xf 的溶液加热至该溶液的泡点 tA,产生第一个气泡的组成为 yA1。 继续加热升高温度,物系变为互 成平衡的汽、液两相,两相温度 相同组成分别为 yA 和 xA 。 当温度达到该溶液的露点,溶液全部汽化成为组成为 yA= xf 的气相,最后一滴液相的组成为 xA2。 y x A,1 A,2 4. 温度——组成图