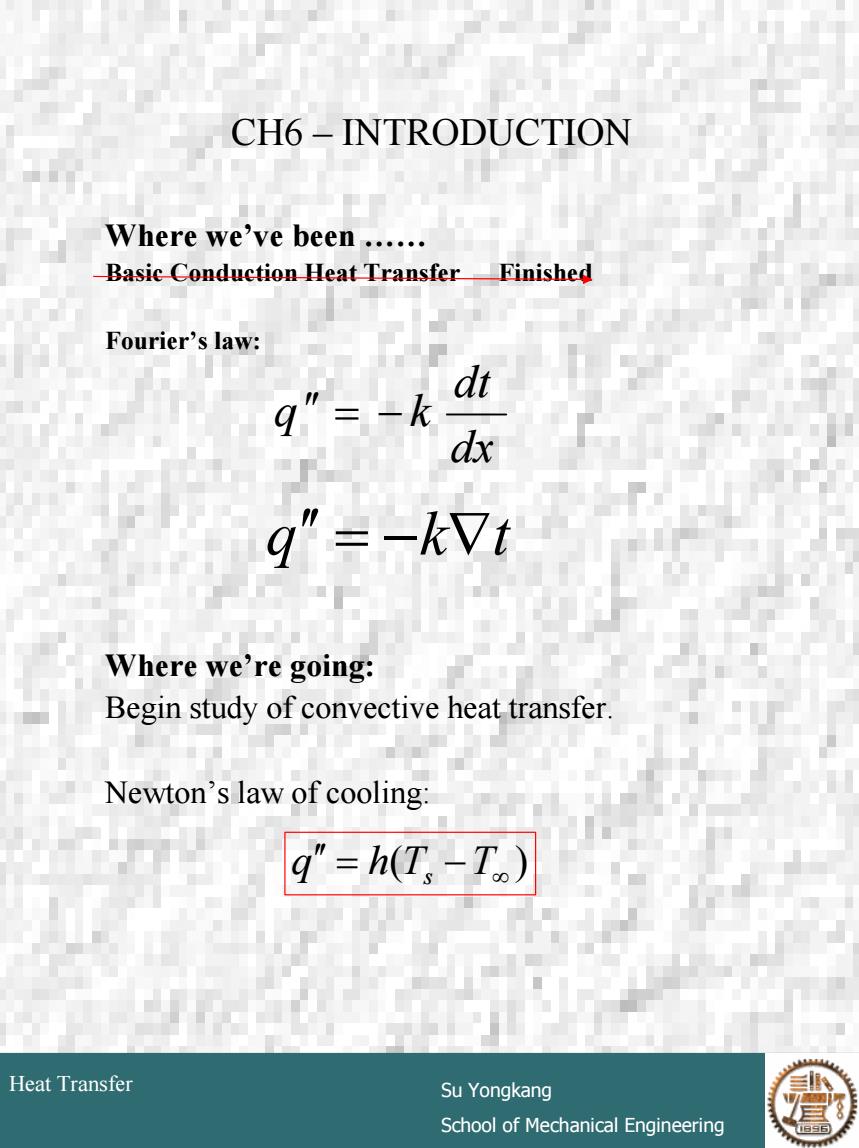
CH6-INTRODUCTION Where we've been...... Basic Conduction Heat Transfer Finished Fourier's law: q"=-k dt dx g"=-kVt Where we're going: Begin study of convective heat transfer. Newton's law of cooling: q"=h(T,-T) Heat Transfer Su Yongkang School of Mechanical Engineering
# 4 Heat Transfer Su Yongkang School of Mechanical Engineering CH6 – INTRODUCTION Where we’ve been …… Basic Conduction Heat Transfer Finished Fourier’s law: Where we’re going: Begin study of convective heat transfer. Newton’s law of cooling: dx dt q ′′ = − k q ′′ = −k∇t ( ) = − ∞ q ′′ h Ts T

Convective transfer problem A FAMILY CIRCUS 2-6 D2o02 BIKeane,nt Dt tyKng Frmn世Srd hEAM FIRCUS. 蒸 "I forget.Does holding the door open let the cold air in,or the warm out?" Heat Transfer Su Yongkang School of Mechanical Engineering
# 5 Heat Transfer Su Yongkang School of Mechanical Engineering Convective transfer problem

CH6 INTRODUCTION KEY POINTS THIS CHAPTER What are the key variables when analyzing convection heat transfer? Review boundary layer concept and significance General idea of relationship between velocity and thermal profiles in a boundary layer. Effect of laminar versus turbulent flow on heat transfer potential Boundary layer similarity This chapter will be taught in two lectures: the first includes text book sections 6.1 to 6.4 the other includes text book sections 6.5 to 6.10 Heat Transfer Su Yongkang School of Mechanical Engineering
# 6 Heat Transfer Su Yongkang School of Mechanical Engineering CH6 INTRODUCTION KEY POINTS THIS CHAPTER • What are the key variables when analyzing convection heat transfer? • Review boundary layer concept and significance • General idea of relationship between velocity and thermal profiles in a boundary layer. • Effect of laminar versus turbulent flow on heat transfer potential • Boundary layer similarity • This chapter will be taught in two lectures: the first includes text book sections §6.1 to 6.4 the other includes text book sections §6.5 to 6.10

Convection overview Consider a flat plate of length L,in air flow with velocity u and temperature To yA 1 1 Local heat flux is: where h is the local heat transfer coefficient q"=h(T,-T) Total heat transfer rate: 9=∫9d4,=(T,-T) hdA. q=hA,(Ts-T) 万= average heat transfer coefficient Determination of h'will rely on analytical as well as empirical data Heat Transfer Su Yongkang School of Mechanical Engineering
# 7 Heat Transfer Su Yongkang School of Mechanical Engineering Convection overview • Consider a flat plate of length L, in air flow with velocity u∞ and temperature T∞ • Local heat flux is: where h is the local heat transfer coefficient • Total heat transfer rate: ( ) = − ∞ q ′′ h Ts T ∫ ∞ ∫ = ′′ = − s As s s A s q q dA (T T ) hdA ( ) q = hAs Ts −T∞ average heat transfer coefficient h = Determination of ‘h’ will rely on analytical as well as empirical data

Convection overview(Cont'd) Same principal applies to any arbitrary shape,not just a flat plate dAs As:Ts Average convection heat transfer coefficient: or,for unit width: d So,we need to know how h varies with x,the distance from the leading edge...... What do you think key parameters that might influence h? Heat Transfer Su Yongkang School of Mechanical Engineering
# 8 Heat Transfer Su Yongkang School of Mechanical Engineering Convection overview (Cont’d) • Same principal applies to any arbitrary shape, not just a flat plate • Average convection heat transfer coefficient: So, we need to know how h varies with x, the distance from the leading edge…….. What do you think key parameters that might influence h? q ′′ dAs As Ts , or, for unit width: ∫ = As s s hdA A h 1 ∫ = L hdx L h 0 1