
§1线性规别的对偶理论 二、对偶规划的求解 1、利用原问题的最优单纯形表求对偶最优解的方法 CB CN 0 b CB XB XB XN Xs CB XB I B-IN -B-1 B-1b 检验数 0 CBB-IN -CN CBB- CBB-Ib
§1线性规划的对偶理论 二、对偶规划的求解 1、利用原问题的最优单纯形表求对偶最优解的方法 cBs xBs c 0 xs 检验数 cB cN 0 xB xN xs B N I cB cN 0 b b 0 cB cB xB xB I B-1N B-1b 0 cBB-1N -cN -cBB-1 cBB-1b -B-1

第四章对偶理论及灵敏度分析 e,g.2求如下LP问题的对偶问题的最优解 max7=4x1+3x2+7x3 ( -4 -3 -7 0 s.tx1+2x2+2x3≤100 CB XB X1 X2 X3 X4 X5 b 3x1+x2+3x3≤100 -3 X2 -3/4 1 0 3/4-1/2 25 x1,X2,3≥0 -7 X3 5/4 0 1-1/4 1/2 25 解 对偶问题为 检验数 -5/2 0 0 -1/2 -2 -250 min w=100y1+100y2 s.ty1+3y2≥4 原问题的最优解和最优值为: 2y1+y2≥3 x*=(0,25,25)7 z*=250 2y1+3y2≥7 Jy1,2≥0 由推论5可知: 对偶问题的最优解和最优值为y*=(1/2,2) w*=250
c cB xB -3 -7 x2 x3 检验数 -4 -3 - 7 0 0 x1 x2 x3 x4 x5 -3/4 1 0 3/4 5/4 0 1 -1/4 -5/2 0 0 -1/2 b 25 25 -250 -1/2 1/2 -2 第四章 对偶理论及灵敏度分析 e.g. 2 求如下 LP 问题的对偶问题的最优解 max z = 4x1+3x2+7x3 s.t. x1+2x2+2x3 ≤100 3x1+ x2+3x3 ≤100 x1 , x2 , x3 ≥ 0 解: 对偶问题为 min w = 100y1+100y2 s.t. y1+ 3y2 ≥4 2y1+ y2 ≥3 2y1+ 3y2 ≥7 y1 , y2 ≥0 原问题的最优解和最优值为: x*=(0,25,25)T z*=250 由推论5可知: 对偶问题的最优解和最优值为 y*= (1/2 , 2) w*= 250
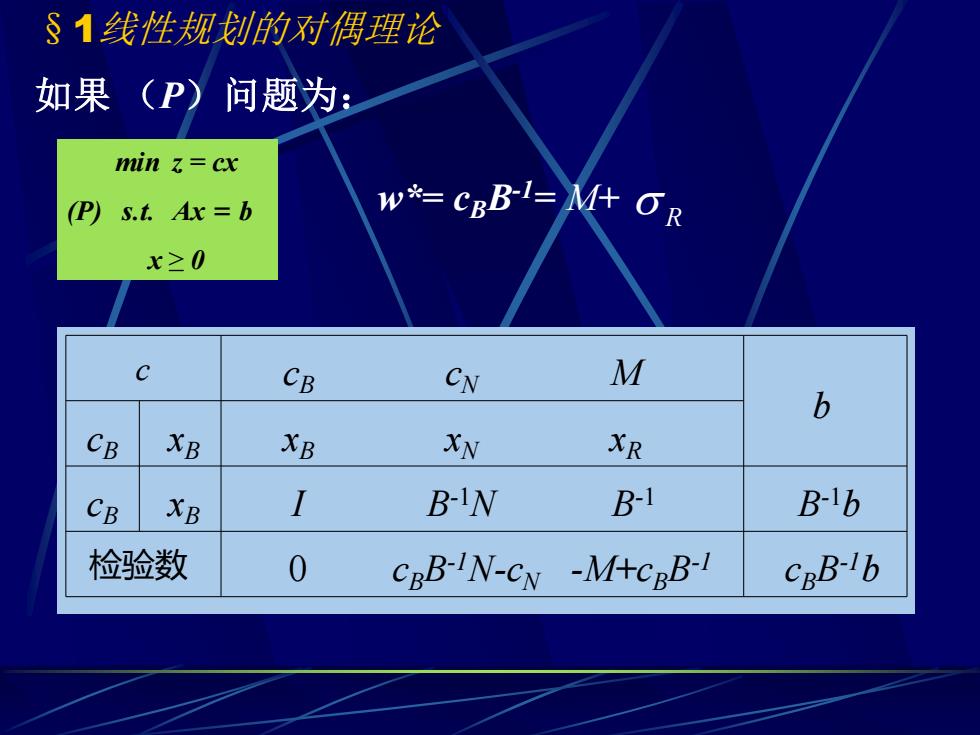
§1线性规划的对偶理论 如果(P) 问题为: min CX (P) s.t.Ax=b w*=cBB1=M什OR x≥0 C CB CN M b CB XB XB XN XR CB XB I BIN B-1 B-ib 检验数 0 cBB-lN-Cw-M什csB-l CBB-Ib
§1线性规划的对偶理论 如果 (P)问题为: min z = cx (P) s.t. Ax = b x ≥ 0 cBs xBs c 0 xs 检验数 cB cN M xB xN xR B N I cB cN -M b b 0 cB cB xB xB I B-1N B-1 B-1b 0 cBB-1N-cN -M+cBB-1 cBB-1b w*= cBB-1= M+ R

第四章对偶理论及灵敏度分析 2、利用互补松弛定理求对偶最优解 a,x-b)=0, i=1,2,…m (c,-Eay)x,=0 j=1,2,…,n eg3求如下LP问题的对偶问题的最优解 mxz=4化1+3x2 解: 对偶问题为: S.tX1+2x2≤2 x12x2≤3 minw=2y1+3y2+5y3+2y4+3y5 2x1+3x2≤5 s.ty1+y2+2y3+y4+3y5≥4 X1+比2≤2 2y12y2+3y3+y+y5≥3 3x1+比2≤3 七1,X2≥0 y1Jy2y3y4小y5≥0
第四章 对偶理论及灵敏度分析 2、利用互补松弛定理求对偶最优解 1 ( ) 0, 1,2, n i ij j i j w a x b i m = − = = 1 ( ) 0, 1,2, , m j ij i j i c a w x j n = − = = e.g. 3 求如下 LP 问题的对偶问题的最优解 max z=4x1+3x2 s.t. x1+2x2 ≤2 x1 -2x2 ≤3 2x1+3x2 ≤5 x1+x2 ≤2 3x1+x2 ≤3 x1 , x2≥ 0 解: 对偶问题为: min w=2y1+3y2+5y3+2y4+3y5 s.t. y1+ y2+2y3+ y4+3y5 ≥4 2y1 -2y2+3y3+ y4+ y5 ≥3 y1 , y2 , y3 ,y4 ,y5 ≥0

§1线性规划的对偶理论 可用图解法求解(P)问题,得:x二(4/5,35)Tz*=5 将x*代入(P)问题的约束条件,知: 约束条件(2)、(3)、(4)成立严格不等式 由互补松弛定理知:2*y*髫*=0 又因为x,*,X2 不为零所以y+*=4 2y,*+J*3 解得:y=y*= m心7=4X1+3x2 s.tK1+2x2≤2 (1) 故y*=(1,0,0,0,1) w*=5 X1-22≤3 (2) min w=2y1+3y2+5y3+2y4+3ys p)2x1+3x2≤5 (3) s.ty1+y2+2y3+y4+3y5≥4 七1+比2≤2 (4) 3x1+x2≤3 (5) (D)2y1r2y2+3y3+y4+y5≥3 七1x2≥0 yy2y3y4y5≥0
§1线性规划的对偶理论 max z=4x1+3x2 s.t. x1+2x2 ≤2 (1) x1 -2x2 ≤3 (2) (p) 2x1+3x2 ≤5 (3) x1+x2 ≤2 (4) 3x1+x2 ≤3 (5) x1 , x2≥ 0 可用图解法求解(P)问题,得:x*=(4/5,3/5)T z*=5 min w=2y1+3y2+5y3+2y4+3y5 s.t. y1+ y2+2y3+ y4+3y5 ≥4 (D) 2y1 -2y2+3y3+ y4+ y5 ≥3 y1 , y2 , y3 ,y4 ,y5 ≥0 将x* 代入(P)问题的约束条件,知: 约束条件(2)、(3)、(4)成立严格不等式 由互补松弛定理知:y2*=y3*=y4*=0 又因为x1* ,x2* 不为零 所以 y1*+3y5* = 4 2y1*+ y5* = 3 解得: y1*= y5* =1 故 y*=(1,0,0,0,1) w*=5