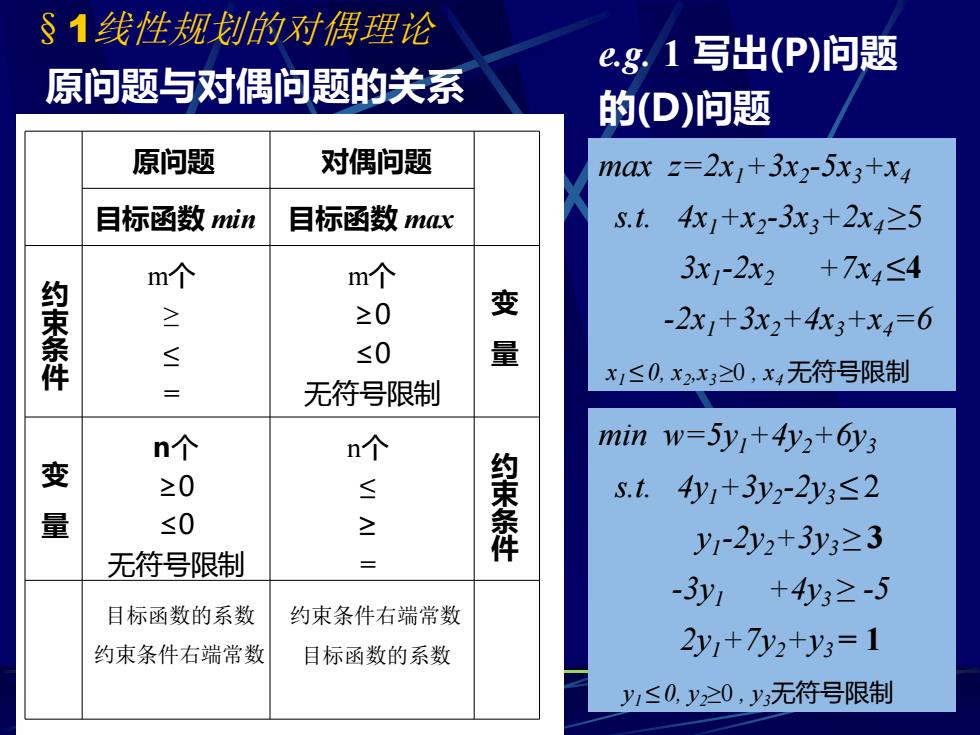
§1线性规的对偶理论 eg.1写出(P)问题 原问题与对偶问题的关系 的(D)问题 原问题 对偶问题 max z=2x+3x2-5x3+x 目标函数min 目标函数max S.t.4x+x2-3x3+2x4≥5 m个 m个 3x-2x2+7x4≤4 约束条件 ≥0 变 -2x1+3x2+43+x4=6 ≤ ≤0 量 x1≤0,x2,x3≥0,x4无符号限制 无符号限制 n个 n个 inw=5y1+4y3+0y3 变 ≥0 ≤ s.t. 4y1+3y2-2y3≤2 量 ≤0 约束条件 y1-2y2+3y3≥3 无符号限制 -3y1+4y3≥-5 目标函数的系数 约束条件右端常数 约束条件右端常数 目标函数的系数 2y1+7y2+y3=1 1≤0,y2≥0,y3无符号限制
§1线性规划的对偶理论 原问题与对偶问题的关系 原问题 目标函数 min 目标函数 max m个 ≥ ≤ = n个 ≤ ≥ = n个 ≥0 ≤0 无符号限制 m个 ≥0 ≤0 无符号限制 目标函数的系数 约束条件右端常数 约束条件右端常数 目标函数的系数 约 束 条 件 约 束 条 件 变 量 变 量 对偶问题 e.g. 1 写出(P)问题 的(D)问题 max z=2x1+3x2 -5x3+x4 s.t. 4x1+x2 -3x3+2x4 ≥5 3x1 -2x2 +7x4 ≤4 -2x1+3x2+4x3+x4=6 x1 ≤ 0, x2 ,x3 ≥0 , x4 无符号限制 min w=5y1+4y2+6y3 s.t. 4y1+3y2 -2y3 ≤ 2 y1 -2y2+3y3 ≥ 3 -3y1 +4y3 ≥ -5 2y1+7y2+y3 = 1 y1 ≤ 0, y2≥0 , y3无符号限制

§1线性规的时偶理论 (P)问题 D 问题 讨论对称形式: min =cx x y=wb s.tAx≥b s.t wA≤C x≥0 w≥0 对偶规划的若干定理 互为对偶 Theorem 1 (对称性定理)对偶问题的对偶是原问题, proof Theorem 2 (弱对偶定理)设x和w0分别是(P)问题和 (D)问题的可行解,则必有 cxW≥w0b proof Corollary1如果x*和w分别是(P)问题和(D)问 题的可行解,且cx=w*b,则x*和w分别是(P)问 题和(D)问题的最优解: 向前
§1 线性规划的对偶理论 讨论对称形式: (P)问题 min z = cx s.t. Ax ≥ b x ≥0 (D)问题 max y= wb s.t. wA ≤ c w ≥0 一、对偶规划的若干定理 Theorem 1 (对称性定理) 对偶问题的对偶是原问题. 互为对偶 proof Theorem 2 (弱对偶定理) 设 x 0 和 w0 分别是(P)问题和 (D)问题的可行解,则必有 c x0 ≥ w0 b . Corollary 1 如果 x * 和 w* 分别是(P)问题和(D)问 题的可行解,且c x * = w* b,则 x * 和 w* 分别是(P)问 题和(D)问题的最优解。 proof 向前

§1线性规的对偶理论 (D)问题 Theorem (对称性定理) max y=wb proof: 先将(D)问题化成原问题形式 s.t wA≤C w≥0 min y=(-b")w s.t. (4)w≥ ≥0 设x为它的对偶变量,写出它的对偶问题 max z =x"(-c") 即 min z=Cx s.tx(-A)≤-b S.t.Ax≥b x≥0 x≥0 这就是(P)问题. 证些
§1 线性规划的对偶理论 Theorem 1 (对称性定理) proof : 先将(D)问题化成原问题形式 min ( ) . . ( ) 0 T T T T T T y b w s t A w c w = − − − (D)问题 max y = wb s.t. wA ≤ c w ≥0 设 x T为它的对偶变量, 写出它的对偶问题 max ( ) . . ( ) 0 T T T T T T z x c s t x A b x = − − − min . . 0 z cx s t Ax b x = 即 这就是(P)问题. 证毕

§1线性规的对偶理论 cx0≥wWb Theorem 2 (弱对偶定理 proof: 因为x是P)问题的可行解,故必有 A4x0≥b,x0≥0 (1 又w是问题(D)的可行解,于是有 w0A≤c,w0≥0 用w0左乘不等式(1)两边,得 w0AxW≥w0b 用x0右乘不等式(2)两边,得 w0AxW≤Cx0 工上 从而有 cxwob I三
§1 线性规划的对偶理论 Theorem 2 (弱对偶定理) proof : 因为 x 0 是(P)问题的可行解, 故必有 Ax 0 ≥ b , x 0 ≥0 (1) 又w0是问题(D)的可行解, 于是有 w0A ≤ c , w0 ≥0 (2) 用w0 左乘不等式 (1) 两边, 得 w0Ax0 ≥ w0b 用x 0 右乘不等式 (2) 两边, 得 w0Ax0 ≤ cx0 从而有 cx0 ≥ w0b 证毕 c x0 ≥ w0 b

第四章对偶理论及灵敏度分析 Corollary2在一对对偶问题中,如果其中一个问题可 行,但目标函数无界,则另一个问题不可行 Corollary3一对对偶问题(P) 和(D)有最优解的充 要条件是它们同时有可行解 Theorem 3 (对偶定理) 如果(P)问题((D) 问题)有 最优解,那么(D)问题((P)问题)也有最优解 且目标函数值相等。 proof Corollary 4 (单纯形乘子定理) 如果(P)问题有最优解 最优基为B,则w*=CBI就是(D)问题的一个最优 解 向前
第四章 对偶理论及灵敏度分析 Corollary 2 在一对对偶问题中,如果其中一个问题可 行,但目标函数无界,则另一个问题不可行。 Corollary 3 一对对偶问题(P)和(D)有最优解的充 要条件是它们同时有可行解。 Theorem 3 (对偶定理) 如果(P)问题((D)问题)有 最优解,那么(D)问题( (P)问题)也有最优解, 且目标函数值相等。 proof Corollary 4 (单纯形乘子定理) 如果(P)问题有最优解, 最优基为 B,则 w* = cBB-1 就是(D)问题的一个最优 解。 向前